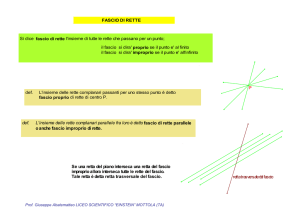
PARALLESISMO - PERPENDICOLARITA' e APPLICAZIONI
TEOREMI FONDAMENTALI
RETTE // TAGLIATE DA UNA TRASVERSALE
def.
Due rette complanari di dicono parallele se non hanno alcun punto in comune, oppure se sono coincidenti; la
parte di piano racchiusa da due rette // si chiama striscia e le due rette parallele sono i bordi della striscia.
La distanza fra le due rette è l'altezza della striscia.
r // s
r
A
distanzafrarette//
punti interni della striscia
s
B
bordi della strisciadella striscia
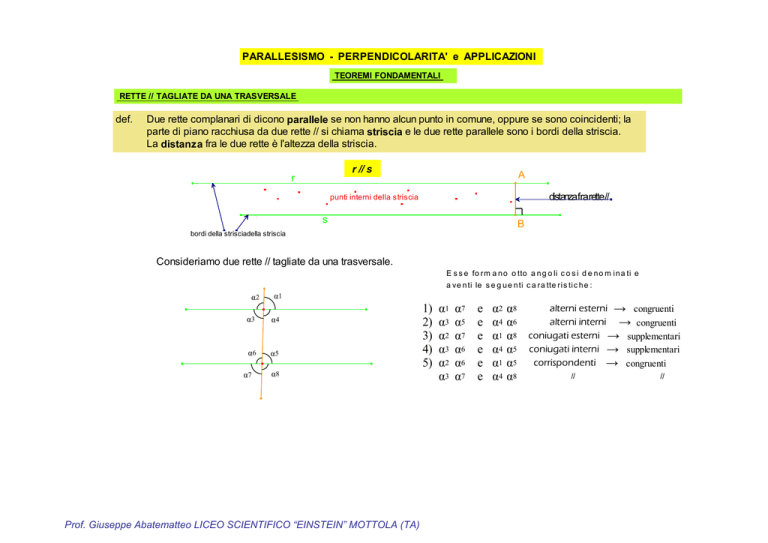
Consideriamo due rette // tagliate da una trasversale.
E s s e fo rm a n o o tto a n g o li c o s i d e n o m i n a ti e
a ve n ti le s e g u e n ti c a ra tte ri s ti c h e :
α2
α1
α3
α4
α6
α5
α7
α8
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
1)
2)
3)
4)
5)
α1
α3
α2
α3
α2
α3
α7
α5
α7
α6
α6
α7
e
e
e
e
e
e
α2
α4
α1
α4
α1
α4
α8
α6
α8
α5
α5
α8
alterni esterni → congruenti
alterni interni → congruenti
coniugati esterni → supplementari
coniugati interni → supplementari
corrispondenti → congruenti
//
//
T
S e è ve ro u n o d e i c in q u e e n u n c ia ti, a llo r a s o n o ve ri g li a ltri q u a ttro .
C rte ri d i p a ra lle lis m o : s e d u e re tte c o m p la n a ri ta g lia te d a u n a tra s ve rs a le fo rm a n o
► u n a c o p p ia d i a n g o li a lte r n i ( e s te r n i o in te r n i) c o n g r u e n ti; opp.
► u n a c o p p ia d i a n g o li c o n iu g a ti ( e s te r n i o in te r n i) c o n g r u e n ti; opp.
► u n a c o p p ia d i a n g o li c o r r is p o n d e n ti c o n g r u e n ti;
a llo r a le d u e r e tte s o n o p a r a lle le .
UNA DELLE SEI OPZIONI è CONDIZIONE NECESSARIA E SUFFICIENE AFFINCHE' DUE RETTE SIANO PARALLELE.
t
d e f.
D u e re tte c o m p la n a ri s i d ic o n o p e r p e n d ic o la r i ( o p p u re o rto g o n a li, o p p . n o rm a li)
r
s e fo rm a n o fo rm a n o q u a ttro a n g o li re tti fra lo ro .
-►
r _|_ s
t
T
Due rette complanari, perpendicolari ad una stessa retta
non hanno alcun punto in comune,
cioè sono parallele.
r
-►
s
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
Postulato di Euclide: Esiste una ed una sola retta // ad una
retta data condotta per un punto esterno ad essa.
t
T
r
Due rette complanari // ad una terza retta sono tra loro //.
-►
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
s
S E M IR E T T E P A R A L L E L E
def.
Si considerino due semirette complanari e // ed una retta che congiunge le loro origini;
► d ir e m o c h e le d u e s e m ir e tte s o n o c o n c o r d i s e g ia c c io n o d a lla s te s s a p a r te d i p ia n o ;
► d ir e m o c h e le d u e s e m ir e tte s o n o d is c o r d i s e g ia c c io n o d a p a r ti o p p o s te d i p ia n o ;
t
t
r
r
A
A
s
s
B
B
SEMIRETTEDISCORDI
SEMIRETTECONCORDI
CONSEGUENZE:
▪ Se due angoli hanno i lati corrispondenti // e concordi (opp. discordi), allora essi sono congruenti;
T
▪ Se due angoli hanno due lati // e concordi, e gli altri due // e discordi, allora essi sono supplementari;
s'
r'
66,0 °
r'
r
r
s'
r
r'
121,0 °
59,0 °
70,0 °
70,0 °
s
LATI CORRISP. // E CONCORDI
66,0 °
s
LATI CORRISP. // E DISs'CORDI
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
59,0 °
s
DUE LATI // E CONCORDI e DUE // E DISCORDI
P R O P R IE T A ' F R A R E T T E P A R A L L E L E
r
A
C
T
Siano r ed s due rette //.
I segmenti // fra loro e compresi fra le due rette, sono fra loro congruenti.
s
B
Ipotesi
se r//s
r
D
A, C € r
B, D € s
AB//CD
A
Tesi
allora AB=CD
Dim. Considera re il 2 ° criterio di congruenza fra i tria ngoli ABD e AD C e le
proprietà degli a ngoli a lterni interni rispetto a lla tra sversa le AD .
C
Conseguenza
T
S i a n o r e d s d u e re tte //.
T u tti i p u n ti d i u n a re tta s o n o e q u i d i s ta n ti d a ll'a ltra .
s
B
D
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)
APPLICAZIONI problemi.
problema N.1 Sia ABC un triangolo isoscele. L'angolo alla base è il doppio dell'angolo al vertice.
Determinare l'ampiezza dell'angolo al vertice.
[36°]
problema N.2 Sia ABC un triangolo isoscele di base BC e angolo al vetrice di 40°. Si prolunghi il lato AB,
dalla parte di B, di un segmento BD =BC e si congiuga C con D .
D eterminare l'ampiezza dell'angolo in D (ADC ) e dell'angolo in C (AC D ).
[35°; 105°]
dim. col cabri.
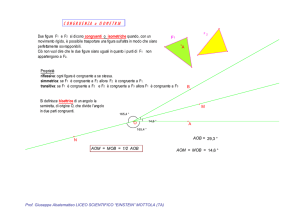
PROPRIETA' CARATTERISTICA DI UN TRIANGOLO RETTANGOLO.
C ondizione Necessaria e Sufficiente affinchè un triangolo sia rettangolo è che
la mediana relativa ad un lato sia congruente alla metà del lato stesso.
In tal caso la mediana ha come vertice quello relativo all'angolo retto ed il lato da cui
parte è l'ipotenusa.
Prof. Giuseppe Abatematteo LICEO SCIENTIFICO “EINSTEIN” MOTTOLA (TA)