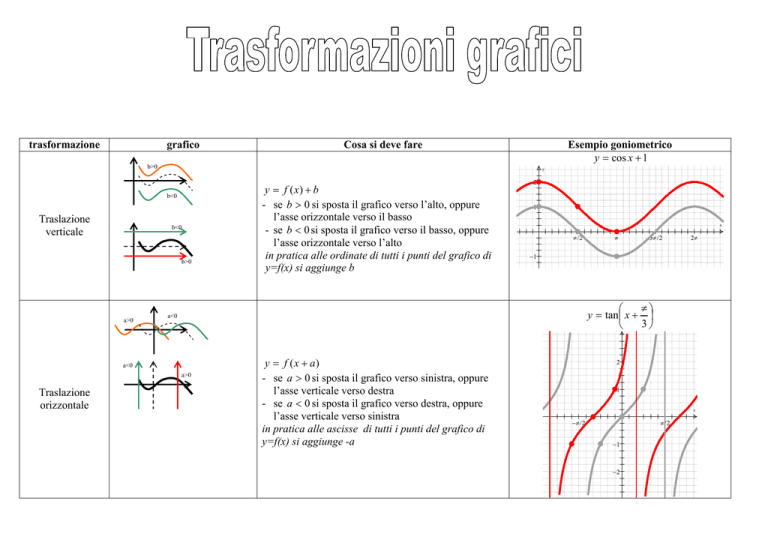
trasformazione
grafico
Cosa si deve fare
Esempio goniometrico
y = cos x + 1
b>0
y
b<0
Traslazione
verticale
b<0
b>0
a>0
y = f ( x) + b
- se b > 0 si sposta il grafico verso l’alto, oppure
l’asse orizzontale verso il basso
- se b < 0 si sposta il grafico verso il basso, oppure
l’asse orizzontale verso l’alto
in pratica alle ordinate di tutti i punti del grafico di
y=f(x) si aggiunge b
2
1
x
π/2
π
3π/2
2π
−1
π
y = tan x +
3
a<0
y
a<0
a>0
Traslazione
orizzontale
y = f ( x + a)
- se a > 0 si sposta il grafico verso sinistra, oppure
l’asse verticale verso destra
- se a < 0 si sposta il grafico verso destra, oppure
l’asse verticale verso sinistra
in pratica alle ascisse di tutti i punti del grafico di
y=f(x) si aggiunge -a
2
1
x
−π/2
π/2
−1
−2
y = − cos x
y
2
Simmetria
rispetto all’asse x
y = − f (x)
in pratica si cambia segno alle ordinate di tutti i punto
del grafico di y=f(x)
1
x
π/2
π
3π/2
2π
−1
−2
y = sin( − x)
y
2
Simmetria
rispetto all’asse y
y = f (− x)
in pratica si cambia segno alle ascissee di tutti i punto
del grafico di y=f(x)
1
x
−π/2
π/2
π
3π/2
−1
−2
y = 2 sin( x)
y
2
Dilatazione
verticale
y = kf (x)
è una dilatazione verticale di k
in pratica si moltiplicano per k le ordinate di tutti i
punto del grafico di y=f(x)
N.B. gli zeri della funzione non cambiano
Non cambia il periodo delle funzioni periodiche
1
x
−π/2
π/2
−1
−2
π
3π/2
y = sin(2 x)
y = f (kx)
è una dilatazione orizzontale di 1/k
Dilatazione
orizzontale
y
2
1
in pratica si moltiplicano per1/ k le ascisse di tutti i
punto del grafico di y=f(x)
x
−π/2
N.B. non cambia l’intercetta della funzione
Cambia il periodo delle funzioni periodiche da T passa
T
a
k
π/2
π
3π/2
−1
−2
y = tan x
3
y
2
Modulo su tutto
y = f (x)
si ribaltano rispetto all’asse x le parti negative
1
x
−π
−π/2
π/2
π
3π/2
−1
−2
y = sin x
3
Modulo su tutte
le x
y = f (x)
si considerano i punti del grafico con le x positive, più
i corrispondenti simmetrici rispetto all’asse delle
ordinate.
N.B. la funzione che si ottiene è certamente
simmetrica rispetto all’asse delle ordinate
y
2
1
x
−π
−π/2
π/2
−1
−2
π
3π/2
C) Ricorda che le funzioni lineari si rappresentano, dopo averle riscritte utilizzando il metodo dell’angolo aggiunto, cioè:
y = a cos x + b sin x = a 2 + b 2 cos( x − α )
a
con α tale che cos α =
e sin α =
2
2
a +b
b
a2 + b2
D) Ricorda che le funzioni di 2° grado si rappresentano dopo aver abbassato di grado utilizzando le formule di duplicazione del coseno e del seno, quindi
1 − cos 2 x
1
1 + cos 2 x
cos 2 x =
sin 2 x =
sin x cos x = sin 2 x
2
2
2
APPLICAZIONI: Traccia i grafici delle seguenti funzioni per ciascuna indica le intersezioni con gli assi cartesiani.
funzione
1
y = 3tg ( x +
2
y=
3
4
5
6
π
6
)
cos x − 2
3
y = 1 − arcsin x
y=
sin 2 x
−1
3
y = arctan( x − 2)
y = arctan x
7
y = 2 cos x − 2 sin x
8
y=
9
y = 1 − sin x cos x
10
11
12
2 − cos 2 x
3
π
y = cos(2 x − )
3
2
y = (cos x + sin x − 1)
3
x
y = arccos( ) + 1
2
Cosa fare per disegnarla
f(x)=0
f(0)
1
tan 3 x
13
y=
14
y = cos 2 x + sin x cos x
15
y = sin 2 x + sin x cos x
Prima di pensare alla soluzione di un problema è necessario fare un disegno accurato!!
TEORIA:
I problemi di trigonometria possono essere di due tipi:
A) Risoluzione di triangoli o poligoni. In genere non è necessario fissare un’incognita, ma serve conoscere i teoremi di trigonometria, le relazioni tra le funzioni
goniometriche e le formule goniometriche. In particolare ricorda che se di un triangolo sono noti tre elementi (almeno uno dei quali è un lato) allora il triangolo si
può risolvere.
B) Problemi nei quali è necessario fissare un’incognita (in genere su un angolo) e in cui si deve risolvere un’equazione o una disequazione oppure tracciare un
grafico.
APPLICAZIONE:
Risolvi i seguenti problemi, specifica se si tratta di problemi del tipo A) o del tipo B) ed indica per ciascuno quali sono le conoscenze teoriche necessarie.
3
24
1) Nel triangolo ABC si ha: sin β = , tan α =
e AB = 10 , determina:
5
7
a) la misura degli altri due lati.
b) Il raggio della circonferenza inscritta
c) Il raggio della circonferenza circoscritta
2) Traccia in una semicirconferenza di diametro AB = 2r la corda AC che forma con AB un angolo il cui coseno è
suo punto di intersezione con il prolungamento del diametro e calcola AD .
4
. Condotta la tangente in C, indica con D il
5
3) E’ dato il segmento AB = 2l . Dal suo punto medio M conduci una semiretta in modo che formi con MB un angolo acuto variabile di ampiezza x. Sia K la
proiezione ortogonale di B sulla semiretta.
2
2
5
a) Risolvi la disequazione AK + KB < l 2 ;
2
2
b) Rappresenta la funzione f ( x) = AK + KB
2
2
2
c) Discuti, all’interno delle limitazioni geometriche lo equazione AK + KB = k
4) E’ dato il triangolo acutangolo ABC di cui si conosce la base AB= 10 , tg BAˆ C =2, tg ABˆ C =3.
a) Calcolare seno e coseno degli angoli  e B̂ e verificare che ACˆ B =45°.
b) Descrivere la semicirconferenza di diametro BC situata, rispetto alla retta BC, nel semipiano non contenente A. Prendere su di essa un punto M e porre
2
CBˆ M =x. Rappresentare la funzione: y = 2
MA + MB
BC
2
2
−
5
4
π
, quello in B è tale che ABˆ D = 2 DBˆ C . Posto DBˆ C = x ,
3
AB BC
3
determina l’espressione analitica della funzione f ( x) =
+
. Risolvi quindi la disequazione f ( x) <
2
AD DC
5) E’ dato il quadrilatero ABCD inscritto in una circonferenza di raggio r. L’angolo in A è di
Nome…………………….Cognome………………………..classe
11 marzo 2008
Verifica di fine corso di recupero di matematica
1) DISEQUAZIONI
sin x(2 cos 2 x + cos x)
a)
< 0 (pti. 2)
tan 2 x − 1
2) GRAFICI
a) y = 1− sin x cos x
(pti. 1)
3) PROBLEMI
b) sin x + 2 cos x − 6 < 0 (pti. 1)
b) y = sin 2 x + sin x cos x (pti. 2)
Traccia in una semicirconferenza di diametro AB = 2r la corda AC che forma con AB un angolo il cui coseno è
punto di intersezione con il prolungamento del diametro e calcola AD .
4
. Condotta la tangente in C, indica con D il suo
5
(pti. 2)
Nome…………………….Cognome………………………..classe
11 marzo 2008
Verifica di fine corso di recupero di matematica
1) DISEQUAZIONI
sin x(2 cos 2 x + cos x)
a)
< 0 (pti. 2)
tan 2 x − 1
2) GRAFICI
a) y = 1− sin x cos x
(pti. 1)
3) PROBLEMI
b) sin x + 2 cos x − 6 < 0 (pti. 1)
b) y = sin 2 x + sin x cos x (pti. 2)
Traccia in una semicirconferenza di diametro AB = 2r la corda AC che forma con AB un angolo il cui coseno è
punto di intersezione con il prolungamento del diametro e calcola AD .
Nome…………………….Cognome………………………..classe
(pti. 2)
11 marzo 2008
Verifica di fine corso di recupero di matematica
1) DISEQUAZIONI
4
. Condotta la tangente in C, indica con D il suo
5
a)
sin x(2 cos 2 x + cos x)
tan 2 x − 1
2) GRAFICI
a) y = 1− sin x cos x
3) PROBLEMI
< 0 (pti. 2)
b) sin x + 2 cos x − 6 < 0 (pti. 1)
(pti. 1)
b) y = sin 2 x + sin x cos x (pti. 2)
Traccia in una semicirconferenza di diametro AB = 2r la corda AC che forma con AB un angolo il cui coseno è
punto di intersezione con il prolungamento del diametro e calcola AD .
(pti. 2)
4
. Condotta la tangente in C, indica con D il suo
5












