Soluzione degli esercizi di riepilogo sul controllo statistico di qualità

Soluzione degli esercizi di riepilogo sul controllo statistico di qualità e sull’ANOVA.
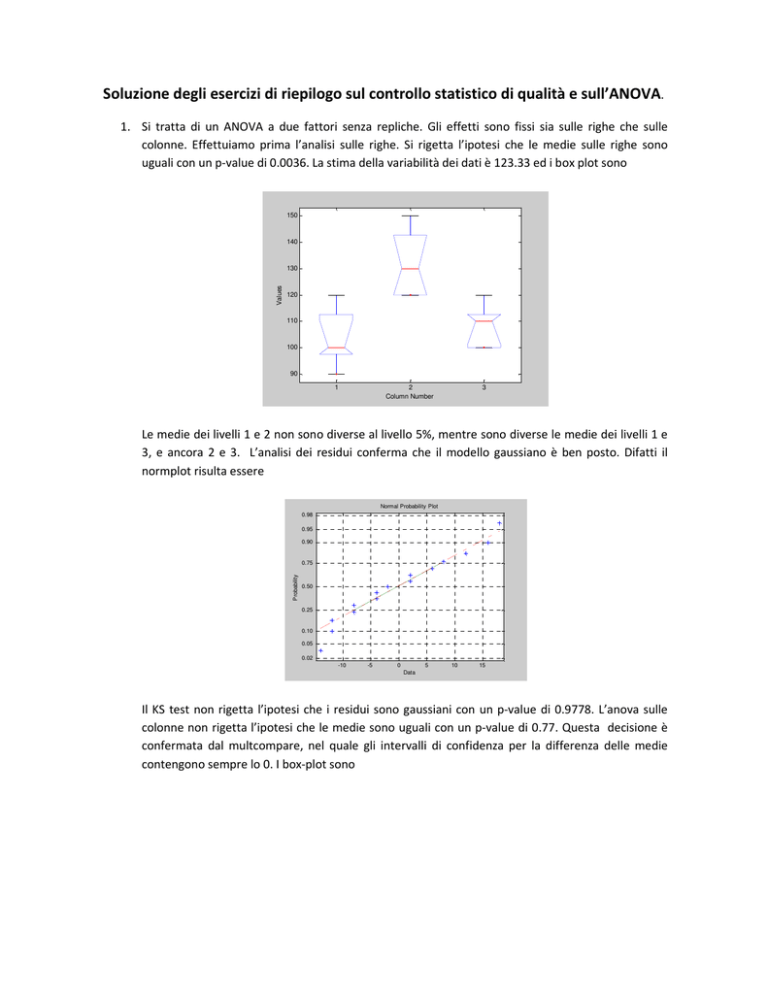
1. Si tratta di un ANOVA a due fattori senza repliche. Gli effetti sono fissi sia sulle righe che sulle
colonne. Effettuiamo prima l’analisi sulle righe. Si rigetta l’ipotesi che le medie sulle righe sono
uguali con un p-value di 0.0036. La stima della variabilità dei dati è 123.33 ed i box plot sono
150
140
Values
130
120
110
100
90
1
2
Column Number
3
Le medie dei livelli 1 e 2 non sono diverse al livello 5%, mentre sono diverse le medie dei livelli 1 e
3, e ancora 2 e 3. L’analisi dei residui conferma che il modello gaussiano è ben posto. Difatti il
normplot risulta essere
Normal Probability Plot
0.98
0.95
0.90
Probability
0.75
0.50
0.25
0.10
0.05
0.02
-10
-5
0
5
10
15
Data
Il KS test non rigetta l’ipotesi che i residui sono gaussiani con un p-value di 0.9778. L’anova sulle
colonne non rigetta l’ipotesi che le medie sono uguali con un p-value di 0.77. Questa decisione è
confermata dal multcompare, nel quale gli intervalli di confidenza per la differenza delle medie
contengono sempre lo 0. I box-plot sono
150
140
Values
130
120
110
100
90
1
2
3
Column Number
4
5
L’analisi dei residui conferma la validità del modello gaussiano:
Normal Probability Plot
0.98
0.95
0.90
Probability
0.75
0.50
0.25
0.10
0.05
0.02
-20
-15
-10
-5
0
5
Data
10
15
20
25
Il Ks test non rigetta l’ipotesi di gaussianità con un p-value di 0.88.
2. La tabella completata risulta essere
(1)
a
b
c
ac
ab
bc
abc
A
-1
1
-1
-1
1
1
-1
1
B
-1
-1
1
-1
-1
1
1
1
C
-1
-1
-1
1
1
-1
1
1
Repliche
9
7
10
12
9
11
11
10
10
13
12
15
10
8
16
14
Somma
16
22
20
21
23
27
18
30
La stima degli effetti risulta essere: effA=3.37, effB=1.62, effC=0.87, effAB=1.3750, effAC=0.1250,
effBC=-0.6250, effABC=1.1250.
Per la stima numerica e grafica delle interazioni AB si ha
B
A
-1
1
-1
9,7,11,10->9.25
10,12,10,8->10
1
9,11,10,8->9.5
12,13,16,14->13.75
14
B=-1
B=1
13.5
13
12.5
12
11.5
11
10.5
10
9.5
9
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
da cui risulta interazione. Per la stima numerica e grafica delle interazioni AC si ha
C
A
-1
1
-1
9,7,9,11->9
10,12,12,13->11.75
1
11,10,10,8->9.75
10,13,16,14->13.25
13.5
C=-1
C=1
13
12.5
12
11.5
11
10.5
10
9.5
9
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
da cui risulta interazione. Per la stima numerica e grafica delle interazioni BC si ha:
C
B
-1
1
-1
9,7,10,12->9.5
9,11,12,13->11.25
1
11,10,10,13->11
10,8,16,14->12
12
C=-1
C=1
11.5
11
10.5
10
9.5
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
la stima numerica e grafica delle interazioni ABC si ha:
(1)
a
b
c
ac
ab
bc
abc
A
-1
1
-1
-1
1
1
-1
1
B
-1
-1
1
-1
-1
1
1
1
C
-1
-1
-1
1
1
-1
1
1
Repliche
9
7
10
12
9
11
11
10
10
13
12
15
10
8
16
14
Media
8
11
10
10.5
11.5
13.5
9
15
16
14
12
10
8
1
0.5
1
0.5
0
0
-0.5
-0.5
-1
-1
Effettuiamo un anovan per completare l’analisi:
Le interazioni non sono statisticamente significative.
3. Bisogna verificare se il campione casuale ha legge gaussiana, nel qual caso si può effettuare un t-test.
altrimenti bisogna effettuare un test sulla mediana.
Il normplot è
Normal Probability Plot
0.98
0.95
0.90
Probability
0.75
0.50
0.25
0.10
0.05
0.02
1700
1800
1900
2000
2100 2200
Data
2300
2400
2500
2600
che non risulta mostrare un andamento lineare. Tuttavia il ks test dei dati standardizzati non rigetta
l’ipotesi di gaussianità con un p-value di 0.51. Pertanto si può effettuare un t-test, visto che non è nota
la varianza della popolazione. L’ipotesi che la media sia 2000 psi non si rigetta, con un p-value molto
basso: 0.06. Questo significa che bisognerebbe fare ulteriori indagini per convalidare la decisione presa.
4. Effettuando un ANOVA2 in Matlab, il valore del p-value per le interazioni è 0.0002. Quindi siamo in
presenza di interazioni dei due fattori e non possiamo proseguire l’analisi. Per via grafica risulta:
8
b1
b2
b3
7
6
5
4
3
2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
da cui si evince che c’è interazione. Per l’analisi dei residui, bisogna calcolare la media di ogni
sottomatrice. Il normplot risulta essere
Normal Probability Plot
0.99
0.98
0.95
0.90
Probability
0.75
0.50
0.25
0.10
0.05
0.02
0.01
-1.5
-1
-0.5
0
Data
0.5
1
1.5
Il Ks test non rigetta l’ipotesi di gaussianità con un p-value 0.24.
5. Bisogna costruire una carta p-value, dove k=30 e ogni sottogruppo ha medesima taglia n=50. La linea
centrale è sul valore 0.08333, il limite inferiore è sul valore 0.0442 e quello superiore è 0.1224. Pertanto
la carta risulta essere:
0.16
0.14
0.12
0.1
0.08
0.06
0.04
0.02
0
5
10
15
20
25
30
Il processo è fuori controllo statistico. L’indice di capacità del processo, in assenza di dati teorici, risulta
essere 1/3, poiché vale 2
p(1 − p )
p (1 − p )
/6
.
n
n
6. Il 25% di 100 è 25. Pertanto abbiamo una popolazione di 100 unità di cui 25 difettose. Da questa
popolazione si estraggono 20 unità senza reimmissione, e l’esercizio chiede di calcolare la probabilità di
trovare al più un pezzo difettoso. Può essere usato un modello stocastico ipergeometrico, con N=100,
K=25, n=20 e x=1, ossia hygecdf(1,100,25,20).
7. Siccome la prestazione obbiettivo è 15, si tratta di un modello NB, per il quale la funzione S/N risulta
valere 7.8576 per la combinazione 1, 10.0709 per la combinazione 2, 14.1940 per la combinazione 3.
Pertanto è da preferire la combinazione 3.
8. E’ possibile usare la carta c:
carta c
10
8
6
4
2
0
-2
-4
0
2
4
6
8
10
12
14
16
18
20
Dall’analisi della carta risulta che il processo è in controllo statistico. Pertanto questi stessi limiti possono
essere usati per monitorare nel seguito il processo.
9. Il diagramma di Pareto in Matlab si costruisce al seguente modo:
>> x=['Lavast';'Sale ';'Brill ';'Acqua ';'Guarni';'Filtri'];
>> y=[45; 7; 2; 25; 60; 30];
>> pareto(y,x)
e il risultato è
160
95%
140
83%
120
71%
100
59%
80
47%
60
36%
40
24%
20
12%
0
Guarni
La funzione perdita ha la forma L ( x) =
Lavast
Filtri
Acqua
0%
Sale
30
( x − 1)2 .
0.252
La probabilità richiesta risulta essere P ( X − 1 > 0.25) = 1 − normcdf (0.25, 0, 7) . Il valore medio invece
risulta E [ L( X ) ] =
30
30
E ( X − 1) 2  =
×7 .
0.25
0.25
10. L’istogramma dei dati risulta essere
Istogramma dei dati
9
8
7
6
5
4
3
2
1
0
96
98
100
102
104
106
108
110
Dall’istogramma, la popolazione da cui sono estratti i dati sembra essere gaussiana. Effettuiamo un ks
test. Il p-value è 0.2555, pertanto l’ipotesi di legge gaussiana non si rigetta.
Effettuiamo un ANOVA a 1 fattore effetti fissi. Dal box-plot, non risulta che i tre turni influenzano la
lunghezza della sbarretta:
110
108
Values
106
104
102
100
98
1
2
Column Number
3
Il P-value dell’ANOVA è infatti 0.90. La variabilità del processo risulta essere 8.26. Non è necessario
effettuare un’analisi dei residui poiché si è già provato che i dati seguono una legge gaussiana.
Per la carta di controllo, si ha
Xbar Chart
110
UCL
108
106
104
CL
102
100
LCL
98
0
5
10
15
Da cui si evince che la produzione è in controllo statistico, per quanto riguarda la media. Per le regole di
zona, si ha
Xbar Chart
110
UCL
108
UCL
4
106
3
6
UCL
104
CL
LCL
102
7
13
14
100
LCL
LCL
98
0
5
10
15
da cui non emergono particolari criticità. La carta dell’escursione scegliamo come limite inferiore il livello 0
e per B il valore 2.57. Si ha
Carta escursione
14
12
10
8
6
4
2
0
0
5
10
15
11. E’ necessario costruire una carta p. Visto che le taglie dei sottocampioni sono diverse, useremo la
taglia media, che risulta essere 98. La linea centrale si attesta su 0.0955. La linea superiore si attesta su
0.1846 e quella inferiore su 0.0064. La carta di controllo risulta essere:
Carta np
0.25
0.2
0.15
0.1
0.05
0
0
5
10
15
Il processo risulta fuori controllo statistico. L’istogramma è
20
25
Istogramma del campione
6
5
4
3
2
1
0
5
10
15
20
mentre il box-plot è
Istogramma del campione
20
Values
15
10
5
1
Column Number
Si tratta dunque di una binomiale asimmetrica (p=0.0955), con una pronunciata coda destra. Per effettuare
un KS test, bisogna costruire il vettore della funzione di ripartizione. Ossia
ccf(:,2)=binocdf(sort(x(:,2)),98,0.0955). Il risultato è
>> [H,P,KSSTAT,CV] = KSTEST(x(:,2),ccf,0.05,0)
H = 0, P = 0.8357, KSSTAT = 0.1207, CV = 0.2641
pertanto l’ipotesi di legge binomiale non si rigetta.
12. La matrice dei coefficienti di correlazione associata ai dati risulta essere:
1.0000 -0.1313 0.8367
-0.1313 1.0000 -0.1599
0.8367 -0.1599 1.0000
Pertanto la coppia povertà vittima è quella che può maggiormente essere modellata con una
regressione lineare. Usando lo strumento polytool, la retta di regressione lineare risulta essere
y = 0.205 +1.011x
40
35
30
25
20
15
10
5
0
-5
-10
6
8
10
12
14
16
18
20
22
24
Il normplot dei residui risulta essere
Normal Probability Plot
0.95
0.90
Probability
0.75
0.50
0.25
0.10
0.05
-4
-2
0
2
Data
4
6
8
Il Ks test non rigetta l’ipotesi di gaussianità dei residui con un p-value di 0.83.
13. La media totale sarà data da X =
da S 2 =
1 20
∑ x j = 33.9cl mentre la varianza campionaria è data
20 j =1
1  20 2 
 ∑ s j  = 10.84 Dai dati del problema si ha che USL = 33(1+ 0.05) = 34,65 mentre
20  j =1 
LSL = 33(1− 0.05) = 31,35. Pertanto si ha:
 34.65 − 33.9 33.9 − 31.35 
C pk = min 
,
 = min{0,0759;0,0735} =0,0735.
9.877 
 9.877