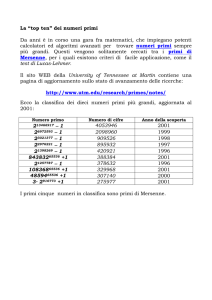
Notizia importante in Teoria dei Numeri:
trovato il più grande numero primo
Gruppo “B. Riemann”*
Francesco Di Noto, Michele Nardelli
*Gruppo amatoriale per la ricerca matematica sui numeri primi, sulle loro
congetture e sulle loro connessioni con le teorie di stringa.
Da “Galileo…”, riportiamo la recente notizia sui numeri primi:
Galileo Giornale di scienza e problemi globali
Temi fisica e matematica
Il più grande numero primo
di Sandro Iannaccone | Pubblicato il 09 Febbraio 2013 12:55
1
I tentativi di battere il record andavano avanti da quattro anni, ormai. E oggi i matematici della
University of Central Missouri di Warrensburg, coordinati da Curtis Cooper, ce l'hanno fatta: sono
riusciti a scoprire il nuovo numero primo più grande mai conosciuto. Conta ben 17.425.170 cifre,
cinque milioni in più rispetto all'ormai ex detentore del primato, scoperto nel 2008 dallo stesso
Cooper.
Per raggiungere lo storico risultato, gli scienziati si sono serviti di una gigantesca rete di computer
messi volontariamente a disposizione dagli utenti (il cosiddetto calcolo distribuito), la Great
Internet Mersenne Prime Search ( Gimps). Il principio è semplice: dato che parte del processore del
proprio computer è generalmente inutilizzato durante le operazioni di routine, gli utenti in rete
decidono di cedere parte della potenza di calcolo della macchina per svolgere operazioni e calcoli,
contribuendo così a un progetto scientifico. Funziona allo stesso modo SETI@Home, in cui sono
scaricati e analizzati i dati dei radiotelescopi per la cosiddetta Search for Extraterrestrial Intelligence
(Seti, per l'appunto, ovvero Ricerca dell'Intelligenza Extraterrestre). Gimps può contare su circa
160mila processori, in grado di eseguire 150 trilioni di calcoli al secondo.
Il numero scoperto, 2 57885161 – 1, fa parte di una categoria particolare di primi, i cosiddetti primi di
Mersenne, scoperti dal monaco francese Martin Mersenne più di 300 anni fa, tutti nella forma 2 p
– 1, dove p è esso stesso un numero primo. Finora, compreso l'ultimo, ne sono stati scoperti solo 48.
“È un'impresa analoga alla scalata dell'Everest”, sostiene George Woltman, informatico in pensione
e fondatore di Gimps: “Le persone provano piacere cercando di scoprire qualcosa fino ad allora
sconosciuta”.
Sebbene il modo più intuitivo di cercare numeri primi possa sembrare quello di dividere ogni
candidato per i numeri minori, non è così: sarebbe troppo dispendioso in termini di tempo
computazionale. “Procedendo in questo modo”, continua Woltman: “si impiegherebbe un tempo più
lungo dell'età dell'Universo”. Al contrario, i matematici hanno messo a punto una strategia molto
più scaltra, che riduce notevolmente il tempo necessario a scovare gli sfuggenti numeri,
permettendo di controllare molti meno divisori.
Oltre alla gloria, la scoperta frutterà a Cooper un premio di 3mila dollari, messo in palio dal
progetto Gimps. In ogni caso, la ricerca di nuovi numeri primi non è, come potrebbe sembrare, un
2
passatempo per matematici smanettoni: tecniche di questo tipo sono infatti molto utilizzate nella
crittografia per effettuare transazioni online in sicurezza. “
Commenti
a) visto che si tratta di un numero di Mersenne, deve necessariamente
essere un numero primo di forma 6k +1 (l’altra forma dei numeri primi,
tranne il 2 e il 3 iniziali, è 6k -1), poiché, essendo una potenza dispari di 2,
come tale ha forma 6k +2, e tolta l’unità nella formula dei numeri di
Mersenne 2p - 1, abbiamo
6k +2 - 1 = 6k +1
Provare per credere!
Esempio per p = 5
25 = 32 = 6*5+2, 32 -1 = 31 = numero primo di
Mersenne per esponente p =5
Esempio per p =7
27= 128 =126 +2, 126 +2 -1 = 127 numero
primo di Mersenne per esponente p =7
Le potenze pari di 2 sono invece di forma 6k – 2, e 6k -2 -1 = numeri
di forma 6k – 3 divisibili per 3 e quindi non possono essere primi, ne
tanto meno numeri primi di Mersenne.
Esempio unico per esponente p = 4 non primo
24 = 16 = 6*3 -2 = 18 -2 = 16, e 16 -1 = 15 = 5*3 e quindi non primo
3
b) nell’articolo riportato, seguono due brevi commenti di due lettori su un
errore
circa l’esponente:
• di Luigi R. , il 09 Febbraio 2013 12:08
Avete sbagliato l'esponente, il numero primo è M57885161. .
● di Gabriele Flamini , il 09 Febbraio 2013 17:10 :
Ho notato che nell'articolo "Il più grande numero primo" viene espressamente detto che
55885161 è un numero primo mentre invece risulta fattorizzabile. Elenco tutti i fattori del
numero p = 55885161: 1-3-53-159-351479-1054437-18628387-55885161.
Ne prendiamo atto, per i nostri lettori che volessero controllare.
c) numero primo successivo : il numero primo N’ (anche non di Mersenne)
successivo a quello appena scoperto, N, dovrebbe trovarsi entro
N + ln (N)2
Essendo 17.425.170 il numero di cifre di N , significa che
N ≈ 1017.425.170, il logaritmo naturale di tale numero è circa
2*17.425.170 = 34 850 340, che , elevato al quadrato (essendo, per la
congettura di Cramer, con recente nostra proposta di dimostrazione
inclusa nel lavoro “PROOF OF ANDRICA’S CONJECTURE AND
MINIMUM GAP BETWEEN TWO CONSECUTIVE PRIMES”, Ing.
Pier Francesco Roggero, Dott. Michele Nardelli, P.A. Francesco Di Noto)
il numero primo successivo a p, entro l’intervallo seguente:
p + (ln p)2; ed essendo 34 850 3402 = 116 178 954 278 115 600, il
numero primo N’ successivo al N = numero di Mersenne
4
recentemente trovato, sarà certamente entro l’intervallo
1017.425.170 + 116 178 954 278 115 600
Tenendo presente però che il numero di Mersenne è almeno
1017.425.170, poiché le 17.425.170 di N non sono tutti zero, ma cifre
tutte diverse tra loro , il prossimo numero primo potrebbe anche
oltrepassare, sebbene di poco, tale intervallo pur non violando la
congettura di Cramer. Ma potrebbe al limite, inferiore, anche essere un
gemello di N , e quindi N’ = N + 2.
Anche qui, provare per credere! E’ difficile, lo sappiamo, per chi è
sprovvisto di supercomputer, e bisognerebbe quindi usare lo stesso
calcolo distribuito del progetto GIMPS.
d) Utilità pratica di numeri primi così grandi.
Probabilmente ancora nessuna, visto che i numeri RSA usati nella
omonima crittografia hanno mediamente qualche centinaio, o al massimo
qualche migliaio di cifre (soprattutto per le applicazioni militari , per
maggiore sicurezza), e assolvono già egregiamente bene il loro compito.
In futuro, non sappiamo ancora a cosa potrebbero servire, non si sa mai.
Attualmente soddisfano solo la curiosità dei cacciatori di primati, e per
premio la modica somma guadagnata di 3000 dollari, che magari però
5
saranno pur qualcosa per qualche giovane precario matematico
smanettone , come dice anche l’Autore della notizia. Con aggiunta di un
po’ di meritata gloria, che non guasta mai.
6