I primi di Mersenne

I primi di Mersenne
Definizione
forma
Si dice primo di Mersenne ogni numero primo avente la
Mk = 2k –1,
dove k è un numero intero maggiore di 1.
Ad esempio M2 = 3 e M3 = 7 sono primi di Mersenne, mentre non è primo
M4 = 24 –1 = 15. È facile dimostrare che, se Mk è primo, allora k deve
essere primo. I successivi primi di Mersenne sono M5 = 31 e M7 = 127.
Originariamente si pensava che Mk fosse primo per ogni valore di k
primo. Ma ciò risultò essere falso: nel 1536 Hudalricus Regius si
accorse infatti che M11 = 2047 = 23  89 non è primo. Questo è solo
l’inizio di una lunghissima serie di controesempi: a tutt’oggi, nonostante
l’impiego di potenti calcolatori, sono stati trovati solo 39 primi di
Mersenne, che riportiamo in tabella. A titolo di curiosità, ricordiamo che
ci sono voluti tre secoli per confutare la convinzione di Mersenne
secondo cui M67 doveva essere primo: solo nel 1903, in una
sorprendente conferenza presso la American Mathematical Society,
Frank Nelson Cole scrisse alla lavagna la decomposizione
267 – 1 = 193 707 721  761 838 257 287.
Applicazioni
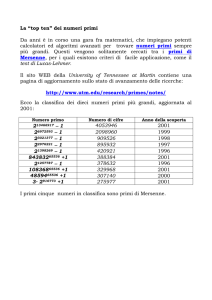
1 Da anni è in corso la gara a chi trova il numero primo più grande.
Ecco l’elenco dei top ten aggiornato al 14 novembre 2001. L’attuale
primato è detenuto da un ricercatore americano appena ventenne.
Osservate che i primi cinque numeri in classifica sono primi di
Mersenne. In effetti, la ricerca di numeri primi di questo tipo è agevolata
da un criterio detto test di Lucas-Lehmer.
2 I primi di Mersenne sono legati ai numeri perfetti.
Definizione Si chiama numero perfetto ogni numero intero positivo che
è somma dei suoi divisori positivi.
Il più piccolo numero perfetto è 6. Per trovare tutti i numeri perfetti pari
si utilizza il seguente teorema, dimostrato da Euclide e da Eulero.
Il numero n è pari e perfetto se e solo se si può scrivere:
n = Mk  2k-1,
per qualche k1, ove Mk è un primo di Mersenne.
Ad ogni primo di Mersenne corrisponde dunque un numero perfetto pari
Pk.
k
Mk
Pk
2
3
6
3
7
28
5
31
496
7
127
8128
Naturalmente, anche i numeri perfetti pari noti sono solo 39.
Fin dall’antichità si sa che i numeri primi sono infiniti (dimostrazione).
Ma non si conosce la risposta al seguente:
Problema irrisolto: Esistono infiniti primi di Mersenne?