INTRODUZIONE ALLA TEORIA DELLA PROBABILITÀ
E DEI PROCESSI ALEATORI
DICAT – Università di Genova
Versione: 1.7
06.09.2011
Luigi Carassale
1
Sommario
1
Teoria della Probabilità ................................................................................................................ 5
1.1
Eventi e spazio campionario.................................................................................................. 5
1.2
Probabilità ............................................................................................................................. 6
1.2.1
Definizione classica (eventi equiprobabili, Laplace, 1812) ........................................... 6
1.2.2
Definizione empirica (frequentista, Von Mises 1920) ................................................... 7
1.2.3
Definizione assiomatica (Kolmogorov 1933) ................................................................ 8
1.3
Teoremi classici della probabilità.......................................................................................... 9
1.3.1
Teorema dell’evento complementare ............................................................................. 9
1.3.2
Teorema dell’evento totale........................................................................................... 10
1.4
Probabilità condizionata e composta ................................................................................... 11
1.5
Variabili Aleatorie ............................................................................................................... 14
1.5.1
Definizione ................................................................................................................... 14
1.5.2
Distribuzione di probabilità ......................................................................................... 14
1.5.3
Funzione di probabilità (di una variabile aleatoria discreta)........................................ 16
1.5.4
Densità di probabilità (di una variabile aleatoria continua) ......................................... 18
1.5.5
Valore atteso ................................................................................................................ 21
1.5.6
Momenti statistici di una variabile aleatoria ................................................................ 23
1.5.7
Funzione caratteristica di una variabile aleatoria continua .......................................... 26
1.5.8
Cumulanti ..................................................................................................................... 26
1.5.9
Entropia ........................................................................................................................ 27
1.5.10 Trasformazioni lineari di variabili aleatorie................................................................. 28
1.5.11 Trasformazioni non lineari di variabili aleatorie.......................................................... 29
1.6
Modelli di variabili aleatorie ............................................................................................... 30
1.6.1
Distribuzione normale (o Gaussiana) ........................................................................... 30
1.6.2
Distribuzione uniforme ................................................................................................ 31
1.6.3
Modello log-normale.................................................................................................... 32
1.6.4
Modello di Rayleigh..................................................................................................... 33
1.6.5
Modello di binomiale ................................................................................................... 33
1.6.6
Modello di Poisson....................................................................................................... 36
2
1.7
1.7.1
Espansione in serie di funzioni ortogonali ................................................................... 37
1.7.2
Principio di massima entropia ...................................................................................... 38
1.7.3
Trasformazione non-lineare di variabili Gaussiane ..................................................... 40
1.8
Rappresentazione della relazione probabilistica fra due grandezze .................................... 43
1.8.1
Distribuzione congiunta di probabilità ......................................................................... 43
1.8.2
Densità congiunta di probabilità .................................................................................. 43
1.8.3
Variabili aleatorie statisticamente indipendenti ........................................................... 45
1.8.4
Valore atteso ................................................................................................................ 46
1.8.5
Somma di variabili aleatorie statisticamente indipendenti .......................................... 46
1.8.6
Correlazione e covarianza ............................................................................................ 46
1.8.7
Modello normale bi-variato ......................................................................................... 49
1.8.8
Distribuzione condizionata di probabilità di una variabile aleatoria ........................... 49
1.9
2
Rappresentazioni approssimate della densità di probabilità................................................ 37
Proprietà delle variabili aleatorie Gaussiane ....................................................................... 51
1.9.1
Indipendenza statistica di variabili non-correlate ........................................................ 51
1.9.2
Linearità dello spazio delle variabili Gaussiane .......................................................... 51
1.9.3
Teorema del limite centrale.......................................................................................... 52
1.9.4
Simmetria polare delle variabili Gaussiane ................................................................. 53
1.9.5
Variabili Gaussiane e cumulanti .................................................................................. 53
1.9.6
Variabili Gaussiane e massima entropia ...................................................................... 54
Vettori Aleatori .......................................................................................................................... 55
2.1
Definizione .......................................................................................................................... 55
2.2
Momenti statistici ................................................................................................................ 55
2.3
Modello normale (Gaussiano) ............................................................................................. 56
2.4
Grandezze statistiche di ordine superiore al secondo .......................................................... 57
2.5
Entropia ed informazione mutua ......................................................................................... 58
2.6
Rappresentazione di vettori aleatori .................................................................................... 58
2.6.1
2.7
3
Analisi a componenti principali (PCA) ........................................................................ 58
Simulazione di vettori Gaussiani ......................................................................................... 60
Processi aleatori ......................................................................................................................... 61
3
3.1
Definizioni ........................................................................................................................... 61
3.1.1
Medie statistiche del primo ordine ............................................................................... 62
3.1.2
Medie statistiche del secondo ordine ........................................................................... 63
3.2
Processi aleatori stazionari .................................................................................................. 63
3.2.1
Medie temporali di una funzione campione ................................................................. 66
3.2.2
Processi aleatori ergodici ............................................................................................. 67
3.2.3
Rappresentazione nel dominio della frequenza di processi stazionari ......................... 67
3.3
Rappresentazione congiunta di una coppia di processi aleatori .......................................... 71
3.3.1
Medie statistiche congiunte del secondo ordine .......................................................... 71
3.3.2
Densità di Potenza spettrale incrociata ........................................................................ 73
3.3.3
Funzione di coerenza ................................................................................................... 73
3.4
Trasformazioni lineari di processi stazionari ...................................................................... 74
3.4.1
4
5
Derivazione di processi stazionari ............................................................................... 76
3.5
Momenti spettrali ................................................................................................................ 77
3.6
Modelli di processi stazionari.............................................................................................. 79
3.6.1
Processo armonico ....................................................................................................... 79
3.6.2
Processo a banda stretta ............................................................................................... 80
3.6.3
Processo a banda estesa................................................................................................ 81
3.6.4
Rumore bianco ............................................................................................................. 82
Analisi statistica di processi aleatori stazionari ......................................................................... 83
4.1
Analisi nel dominio del tempo - stima della funzione di autocorrelazione ......................... 84
4.2
Analisi nel dominio della frequenza - stima della funzione densità di potenza spettrale ... 84
Simulazione di processi aleatori ................................................................................................ 87
5.1
Metodo di Shinozuka........................................................................................................... 87
Equation Chapter (Next) Section 1
4
1
Teoria della Probabilità
Il concetto di probabilità, utilizzato a partire dal '600, è diventato con il passare del tempo la base di
diverse discipline scientifiche. I primi studi che portarono successivamente a concetti legati alla
probabilità possono essere trovati a metà del XVI secolo in Liber de ludo aleæ di Girolamo Cardano
(scritto nel 1526, ma pubblicato solo un secolo e mezzo dopo, nel 1663) e in Sulla scoperta dei dadi
di Galileo Galilei (pubblicato nel 1656). In particolare, Galileo spiegò il motivo per cui, lanciando
tre dadi, il 10 sia più probabile del 9 nonostante che entrambi i risultati si ottengano da un uguale
numero di combinazioni.1
La nascita del concetto moderno di probabilità viene attribuita a Blaise Pascal (1623-1662) e Pierre
de Fermat (1601-1665).2 Nel 1657 Christiaan Huygens (1629-1695) scrisse un Libellus de
ratiociniis in ludo aleæ, il primo trattato sul calcolo delle probabilità, nel quale introduceva il
concetto di valore atteso. Nel 1713 viene pubblicato postumo Ars conjectandi di Jakob Bernoulli,
dove veniva dimostrato il teorema che porta il suo nome, noto anche come legge dei grandi numeri.
Successivamente, de Moivre pervenne ad una prima formulazione, poi generalizzata da Pierre
Simon Laplace (1749-1827), del Teorema del limite centrale. La teoria della probabilità raggiunse
così basi matematicamente solide e, con esse, il rango di nuova disciplina.
1.1 Eventi e spazio campionario
In teoria della probabilità si considera un fenomeno osservabile esclusivamente dal punto di vista
della possibilità o meno del suo verificarsi, prescindendo dalla sua natura. Un ruolo centrale in
questo contesto è svolto dal concetto di evento.
Si consideri una singola osservazione o misura di un fenomeno (es. la tensione di snervamento in un
provino metallico soggetto alla prova di trazione, il numero di studenti in un aula, la velocità del
vento in un determinato luogo e in un dato istante). Se il fenomeno in esame è deterministico, il
risultato dell’osservazione (o dell’esperimento) può essere predetto con esattezza. Se il fenomeno è
aleatorio, il risultato dell’osservazione non è noto a priori; tuttavia è possibile identificare un
insieme , che contiene tutti i possibili risultati dell’esperimento. L’insieme è chiamato spazio
campionario; gli elementi di sono detti punti campionari.
Si definisce evento, E, un insieme di punti campionari (e quindi di risultati possibili
dell’osservazione). Lo spazio campionario Ω contiene tutti i possibili punti campionari, quindi gli
eventi sono sottoinsiemi dello spazio campionario. Si definisce evento elementare l’evento che
contiene un solo punto campionario; evento certo, quello che contiene tutti i punti campionari (cioè
coincide con lo spazio campionario); evento impossibile, quello che non contiene punti campionari.
Gli eventi vengono normalmente indicati con lettere maiuscole. Dati due eventi A e B, si indica con
AB la loro unione, ovvero l'evento costituito dal verificarsi dell'evento A oppure dell'evento B. Si
indica con AB la loro intersezione, ovvero l'evento costituito dal verificarsi sia dell'evento A che
1
Il 9 si ottiene con le sei combinazioni (1,2,6), (1,3,5), (1,4,4), (2,2,5), (2,3,4), (3,3,3), il 10 con le sei combinazioni
(1,3,6), (1,4,5), (2,2,6), (2,3,5), (2,4,4), (3,3,4). Tuttavia, mentre una combinazione di tre numeri uguali può presentarsi
in un solo modo, una con due numeri uguali può presentarsi in tre modi diversi, una con tre numeri diversi in sei modi
diversi. Si può quindi ottenere il 10 in 27 modi (6+6+3+6+3+3), il 9 in 25 modi (6+6+3+3+6+1).
2
Il Cavalier de Méré (un accanito giocatore passato alla storia per questo) aveva calcolato che ottenere almeno un 6 in 4
lanci di un dado era equivalente ad ottenere almeno un doppio 6 in 24 lanci. Tuttavia, visto che giocando secondo tale
convinzione invece di vincere perdeva, scrisse a Pascal lamentando che la matematica falliva di fronte all'evidenza
empirica. Da ciò scaturì una corrispondenza tra Pascal e Fermat in cui iniziò a delinearsi il concetto di probabilità
nell'accezione frequentista.
5
dell'evento B. Se AB = i due eventi A e B vengono detti mutuamente esclusivi o incompatibili
(non possono verificarsi simultaneamente). Il complemento di un evento A rispetto a Ω, Ω\A, è detto
negazione di A e indica il suo non verificarsi (ovvero il verificarsi dell'evento complementare).
Esempio 1.1. Eventi.
Nel lancio di un dado, i possibili risultati sono i numeri 1, 2, … 6. Ognuno è un punto
campionario ω dello spazio campionario Ω = {1, 2, 3, 4, 5, 6}. Si considerino i seguenti
eventi:
A = “occorrenza di un numero pari” = 2,4, 6;
B = “occorrenza di un numero dispari” = 1, 3, 5;
C = “occorrenza del numero 2” = 2;
D = “occorrenza del numero 7” = ;
E = AB = ;
A e B sono eventi incompatibili;
C è un evento elementare, D è un evento impossibile, E è l’evento certo.
1.2 Probabilità
Esistono diverse definizioni di probabilità. Nel seguito si forniranno 3 definizioni che hanno rilievo
per la loro importanza storica o utilità pratica.
1.2.1 Definizione classica (eventi equiprobabili, Laplace, 1812)
Secondo la prima definizione di probabilità, per questo detta classica, la probabilità P(A) di
occorrenza dell’evento A è definita come:
P A
NA
N
(1.1)
dove N è il numero di risultati possibili (assumendo che siano equiprobabili) e NA è il numero di
risultati favorevoli all’evento A.
Esempio 1.2. Definizione classica di probabilità
Lancio di una moneta Ω = {T, C}; sia A:=T, allora P(A) = 1/2;
Lancio di un dado Ω = {1, 2,…,6}; sia A = {1, 2}, allora P(A) = 2/6 = 1/3;
Estrazione numero roulette: Ω = {0, 1,…,90}; sia A = “estrazione numero dispari” = {1,
3,…,89}, allora P(A) = 45/91.
La definizione classica consente di calcolare effettivamente la probabilità in molte situazioni.
Inoltre, è una definizione operativa e fornisce quindi un metodo per il calcolo. Presenta tuttavia
diversi aspetti negativi non irrilevanti:
si applica soltanto a fenomeni con risultati equiprobabili;
presuppone un numero finito di risultati possibili;
la definizione è circolare perché utilizza la nozione di probabilità (eventi equiprobabili) per
definire la probabilità stessa.
6
1.2.2 Definizione empirica (frequentista, Von Mises 1920)
Per superare tali difficoltà, Richard von Mises (1883-1953) propose di definire la probabilità di un
evento come il limite cui tende la frequenza relativa dell'evento al crescere del numero degli
esperimenti. Si consideri un esperimento che possa essere ripetuto un numero infinito di volte e si
assuma che un evento E si sia verificato un numero nE di volte durante l’esecuzione di n
esperimenti. La probabilità di occorrenza dell’evento E si definisce come il limite per n che tende a
infinito della sua frequenza relative nE/n:
P E lim
n
nE
n
(1.2)
Esempio 1.3. Definizione frequentista di probabilità: convergenza alla definizione classica
Si simuli il lancio di un dado e si verifichi mediante la definizione (1.2) che l’evento A =
{1, 2} ha probabilità 1/3.
Il codice Matlab riportato in Figura 1-1 genera una successione di numeri casuali, x,
mediante il comando rand. I valori di x così generati sono compresi nell’intervallo chiuso
[2-53, 1-2-53]. A partire da x, il codice genera numeri interi, y, casuali equiprobabili compresi
fra 1 e 6.
La Figura 1-2 mostra i primi 10 risultati di una sequenza casuale. La Figura 1-3 mostra la
convergenza della probabilità calcolata mediante la definizione frequentista al valore
ottenuto dalla definizione classica (1/3). Si osserva che per avere una buona corrispondenza
fra i due valori sono necessari circa 104 esperimenti.
% Convergenza definizione frequentista probabilità
%
%
%
%
%
%
Esempio: lancio di un dado
n = numero esperimenti
A = evento
y = risultati esperimenti
fA = elenco eventi favorevoli (1) e sfavorevoli (0)
PA = probabilità di occorrenza evento A
n = 1e6;
x = rand(n,1);
y = round(6 * x + 0.5);
A = [1 2];
fA = zeros(n,1);
for k=1:n
fA(k) = sum(A==y(k));
end
PA = cumsum(fA) ./ (1:n)';
figure(1)
plot(1:10,y(1:10),'xr')
ylim([0 7])
grid on
xlabel('j')
ylabel('y_j')
figure(2)
semilogx(1:n,PA, 1:n, ones(n,1)*length(A)/6,'r--')
xlabel('n')
ylabel('n_E/n')
grid on
set(gca,'xMinorGrid','off')
Figura 1-1. Codice Matlab per verifica convergenza definizione frequentista di probabilità.
7
7
6
5
yj
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10
j
Figura 1-2. Lancio di un dado: punti campionari corrispondenti a 10 esperimenti.
0.45
0.4
0.35
0.3
nE/n
0.25
0.2
0.15
0.1
0.05
0
0
10
1
10
2
10
3
10
n
4
10
5
10
6
10
Figura 1-3. Convergenza della frequenza relativa al valore della probabilità definita mediante
la (1.1).
La definizione frequentista, come quella classica, è operativa, cioè consente di calcolare
praticamente la probabilità di eventi in molte circostanze; inoltre, è coerente con quanto fornito
dalla definizione classica nel caso di eventi equiprobabili. Tuttavia è necessario osservare:
il "limite" delle frequenze relative non corrisponde all'analogo concetto matematico; ad
esempio, data una successione {an}, si dice che a è il suo limite se per ogni ε > 0 esiste un
numero naturale N tale che |an - a| < ε per ogni n > N, e, comunque dato ε, è sempre
possibile calcolare N; nella definizione frequentista, invece, N non è sempre calcolabile;
non tutti gli esperimenti sono ripetibili; ad esempio, ha sicuramente senso chiedersi quale sia
la probabilità che vi sia vita su Marte o che tra 50 anni il tasso di natalità in Africa diventi la
metà di quello attuale, ma in casi simili non è possibile immaginare esperimenti ripetibili
all'infinito.
1.2.3 Definizione assiomatica (Kolmogorov 1933)
L'impostazione assiomatica della probabilità venne proposta da Andrey Nikolaevich Kolmogorov
nel 1933 in Grundbegriffe der Wahrscheinlichkeitsrechnung (Concetti fondamentali del calcolo
delle probabilità). Va notato che la definizione assiomatica non è una definizione operativa e non
fornisce indicazioni su come calcolare la probabilità. Il nome deriva dal procedimento per
"assiomatizzazione" basato sull'individuare di concetti primitivi, da cui individuare i postulati e, per
via deduttiva, i teoremi.
8
L'impostazione assiomatica muove dal concetto di σ-algebra, o classe additiva. Dato un qualsiasi
esperimento casuale, i suoi possibili risultati costituiscono gli elementi di un insieme non vuoto Ω,
detto spazio campionario, e ciascun evento è un sottoinsieme di Ω. La probabilità viene vista, in
prima approssimazione, come una misura, cioè come una funzione che associa a ciascun
sottoinsieme di Ω un numero reale non negativo tale che la somma delle probabilità di tutti gli
eventi sia pari a 1.
Si assuma che ogni evento nello spazio campionario sia associato a un numero reale P(E),
chiamato probabilità di E. Questo numero soddisfa le tre seguenti condizioni:
1. La probabilità è un numero non-negativo: P(E) ≥ 0;
2. La probabilità dell’evento certo è unitaria: P(Ω) = 1;
3. Dati due eventi A e B definiti come mutuamente esclusivi, allora P(AB) = P(A) + P(B).
Si osservi che, come conseguenza degli assiomi precedenti, necessariamente, P(E) 1.
I tre assiomi introdotti da Kolmogorov sono coerenti con la definizione empirica fornita da Von
Mises e con la definizione classica enunciata da Laplace.
1.3 Teoremi classici della probabilità
Dagli assiomi precedenti si ricavano i teoremi di seguito riportati.
1.3.1 Teorema dell’evento complementare
Si definisce evento complementare Ec = \E dell’evento E, l’evento che comprende tutti i punti
campionari di Ω non compresi in E (Figura 1-4).
Ec
E
Figura 1-4. Evento complementare.
Un evento E e il suo complementare Ec sono mutuamente esclusivi, cioè la loro intersezione
fornisce l’evento vuoto, mentre la loro unione genera l’evento certo
E Ec 0
E Ec
(1.3)
Applicando alla (1.3) l’Assioma 3 si deduce:
P Ec 1 P E
(1.4)
In particolare, essendo Ωc = , l’applicazione della (1.4) dimostra che l’evento vuoto ha probabilità
di occorrenza zero (P(0) = 0). La (1.4) e l’assioma 1 dimostrano che P(E) 1.
9
Esempio 1.4. Probabilità dell’evento complementare
Sia P = 10-6 la probabilità di collasso di una struttura in un anno. La probabilità che tale
struttura non collassi in un anno è 1 – P = 1 – 10-6.
1.3.2 Teorema dell’evento totale
Il teorema della probabilità totale consente di calcolare la probabilità dell'unione di due, ovvero la
probabilità che si verifichi almeno uno di essi. Essa è la somma delle probabilità dei singoli eventi
se sono mutuamente esclusivi; in caso contrario, alla somma va sottratta la probabilità
dell’intersezione. Si consideri due eventi E1 e E2 in (Figura 1-5):
E1E2
E1
E2
Figura 1-5. Evento totale.
L’unione degli eventi E1 e E2 può essere scritta come:
E1 E2 E1 E2 E2 E1 E1 E2
(1.5)
dove (E1 – E2) contiene i punti campionari presenti in E1, ma non in E2 (E2 – E1 è definito
analogamente). I tre eventi rappresentati dagli insiemi del termine di destra della (1.5) sono
mutuamente esclusivi, quindi per l’Assioma 3 risulta:
P E1 E2 P E1 E2 P E2 E1 P E1 E2
(1.6)
Da Figura 1-5 risulta inoltre che E1 E1 E2 E1 E2 . La probabilità di occorrenza
dell’evento E1 – E2 risulta pertanto:
P E1 E2 P E1 P E1 E2
(1.7)
Sostituendo la (1.7) (e un’espressione analoga per E2 – E1) nella (1.6), la probabilità di occorrenza
dell’evento totale E1 E2 risulta:
P E1 E2 P E1 P E2 P E1 E2
(1.8)
Dalla (1.8) e dall’assioma di positività discende la condizione:
P E1 E2 P E1 P E2
(1.9)
10
Esempio 1.5. Probabilità dell’evento totale.
Si consideri il lancio di un dado e si considerino i seguenti eventi:
E1 1, 2,3;
E2 3, 4;
1,
,6
Applicando la definizione (1.1) risulta:
P E1 1 2
P E2 1 3;
P E1 E2 1 6
Applicando il teorema dell’evento totale risulta:
P E1 E2 P E1 P E2 P E1 E2 2 3
1.4 Probabilità condizionata e composta
Si dice probabilità condizionata di A dato B, e si scrive P(A|B), la probabilità che l'evento A ha di
verificarsi quando si sappia che B si è verificato.
P A | B
P A B
P B
P B 0
(1.10)
La definizione di probabilità condizionata può essere facilmente spiegata considerando il caso di
uno spazio campionario contenente N punti campionari equiprobabili . Sia NB il numero di
risultati favorevoli per l’evento B e NAB il numero di risultati favorevoli contemporaneamente per
gli eventi A e B (e quindi per l’evento A B). Sostituendo nella (1.10) la definizione classica di
probabilità (Eq. (1.1)):
P A | B
N AB N N AB
N NB NB
(1.11)
La probabilità condizionata P(A|B) può essere dunque interpretata come la probabilità di occorrenza
di A nello spazio campionario ridotto determinato da B (Figura 1-6).
B
A
Figura 1-6. Probabilità condizionata.
Esempio 1.6. Probabilità condizionata.
Si consideri il lancio simultaneo di due dadi. Si voglia determinare la probabilità di
occorrenza del numero 7 (evento A), dato che uno dei due dadi ha fornito il numero 1
(evento B). Lo spazio campionario contiene i 36 punti campionari equiprobabili:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6).
11
Il numero di risultati favorevoli a A è NA = 6, quindi P(A) = 1/6; il numero di risultati
favorevoli a B è NB=11, quindi P(B) = 11/36; il numero di risultati favorevoli
simultaneamente ad A e B è NAB = 2, quindi P(AB) = 1/18; il numero di risultati
favorevoli a A, dato che si è verificato B sono 2 su 11 possibilità, quindi P(A|B)=2/11.
Attraverso il concetto di probabilità condizionata si perviene al teorema della probabilità composta,
che consente di calcolare la probabilità dell'intersezione di due o più eventi, ovvero la probabilità
che essi si verifichino entrambi. Nel caso di due eventi, si ha
P A B P A | B P B P B | A P A
(1.12)
Nel caso che la probabilità di A dato B, P(A|B), sia uguale a P(A), i due eventi vengono definiti
stocasticamente (o probabilisticamente, o statisticamente) indipendenti e dalla stessa definizione
segue una diversa formulazione della probabilità composta, caso particolare del precedente:
P A B P A P B
(1.13)
Esempio 1.7. Eventi statisticamente indipendenti.
Si consideri i seguenti eventi legati al lancio di un dado:
1, 2,3, 4,5,6;
A 1, 2;
B 1,3,5;
C 2, 4,6
P A 2 / 6;
P B 3/ 6;
P C 3/ 6 ;
A B 1,
P A B 1/ 6 P A P B A, B indipendenti;
B C ,
P B C 0 P B P C B, C dipendenti.
Si osserva che gli eventi A e B sono indipendenti, ma non mutuamente esclusivi, mentre gli
eventi B e C sono mutuamente esclusivi, ma non indipendenti. Si potrebbe osservare, in
proposito, che due eventi mutuamente esclusivi non possono essere statisticamente
indipendenti, in quanto la realizzazione di uno comporta la non-realizzazione dell’altro.
Il codice Matlab riportato in Figura 1-7 valuta, applicando la definizione frequentista, la
probabilità di occorrenza dell’evento A = {1, 2} e la probabilità di occorrenza di A
condizionata all’occorrenza di B = {2, 4, 5}. La Figura 1-8 mostra che, all’aumentare del
numero di esperimenti n, le probabilità P(A) e P(A|B) tendono al medesimo valore. Ciò
indica che gli eventi A e B sono statisticamente indipendenti.
12
%
%
%
%
%
%
%
%
%
%
%
%
Esempio: lancio di un dado
verifica che gli eventi A = [1 2] e B = [2 4 5] sono statisticamente
indipendenti.
n = numero di esperimenti
y = risultati esperimenti (lanci dado)
fA = elenco eventi favorevoli (1) e sfavorevoli (0) per A
fB = elenco eventi favorevoli (1) e sfavorevoli (0) per B
fAB = elenco eventi favorevoli (1) e sfavorevoli (0) per A e B
contemporaneamente
PA = probabilità di occorrenza evento A
PAcB = probabilità di occorrenza di A dato B
n = 1e5;
x = rand(n,1);
y = round(6 * x + 0.5);
A = [1 2];
B = [2 4 5];
fB = zeros(n,1);
fAB = zeros(n,1);
for k=1:n
fA(k) = sum(A==y(k));
fB(k) = sum(B==y(k));
fAB(k) = sum(A==y(k)) & sum(B==y(k));
end
PA = cumsum(fA) ./ (1:n)';
PAcB = cumsum(fAB) ./ cumsum(fB);
Figura 1-7. Codice Matlab per verifica indipendenza statistica mediante definizione
frequentista di probabilità.
0.5
0.45
0.4
P(A), P(A|B)
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
0
10
10
1
10
2
10
3
10
4
10
5
n
Figura 1-8. Probabilità di A (linea blu), e probabilità di A dato B (linea rossa).
13
1.5 Variabili Aleatorie
In teoria della probabilità, una variabile casuale (o variabile aleatoria o variabile stocastica o
random variable) può essere pensata come il risultato numerico di un esperimento quando questo
non è prevedibile con certezza (ossia non è deterministico). Ad esempio, il risultato del lancio di un
dado può essere matematicamente modellato come una variabile casuale che può assumere uno dei
sei possibili valori 1, 2, 3, 4, 5, 6. Bruno de Finetti definiva numero aleatorio (termine suggerito
dallo stesso per denotare la variabile casuale) un numero ben determinato ma non noto per carenza
di informazioni.
1.5.1 Definizione
Dato uno spazio campionario Ω su cui è definita una misura di probabilità, una variabile aleatoria è
una funzione (misurabile) dallo spazio campionario a uno spazio misurabile (es. l’insieme dei
numeri naturali, l’insieme dei numeri reali, ecc.; Figura 1-9).
In questo capitolo, si considerano variabili aleatorie a valori scalari (dette mono-variate). Variabili
aleatorie a valori vettoriali sono definite nei capitoli successivi.
Una variabile aleatoria è definita continua se ha valori in intervalli continui di . Una variabile è
detta discreta si ha valori in un insieme di numeri finito o numerabile (es. ). Una variabile
aleatoria è detta mista se assume valori in un insieme continuo, ma possiede un numero discreto di
valori aventi probabilità di occorrenza finita.
Nel seguito, le variabili aleatorie verranno indicate con lettere maiuscole (es. X), mentre le
corrispondenti lettere minuscole (es. x) verranno utilizzare per identificare generici valori assunti da
X, detti realizzazioni. La realizzazione x può essere interpretata come l’immagine del punto
campionario attraverso X (Figura 1-9).
x = X()
x
Figura 1-9. Variabile aleatoria X.
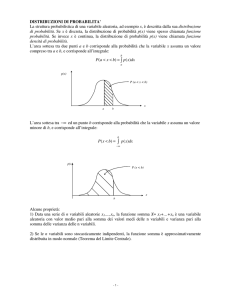
1.5.2 Distribuzione di probabilità
La distribuzione di probabilità (o distribuzione cumulative, o cumulative distribution function,
CDF) è una funzione che definisce la probabilità che la variabile aleatoria X assuma valori minori o
uguali ad un parametro in .
FX P X
(1.14)
La distribuzione di probabilità è definite per qualsiasi valore dell’argomento in e possiede le
seguenti proprietà (facilmente deducibili dalla (1.14) e dagli assiomi della teoria della probabilità):
FX P X P 0
(1.15)
FX P X P 1
(1.16)
14
P 1 X 2 FX 2 FX 1
1 2
(1.17)
Dalla (1.17) discende (per l’assioma di positività) che la distribuzione di probabilità è una funzione
non-decrescente i cui valori appartengono all’intervallo chiuso [0, 1]. Sarebbe possibile dimostrare
anche l’implicazione inversa: una funzione non-decrescente che soddisfa le condizioni (1.15) e
(1.16) rappresenta la distribuzione di probabilità di una qualche variabile aleatoria.
Esempio 1.8. Stima distribuzione di probabilità di una variabile aleatoria discrete
La Figura 1-10 mostra il codice Matlab per la stima della distribuzione di probabilità di una
variabile aleatoria discreta X, rappresentativa dei risultati del lancio di un dado. La Figura
1-11 mostra la distribuzione di probabilità stimata. Si osserva la struttura discontinua della
funzione, tipica delle variabili aleatorie discrete. I salti nella funzione rappresentano
probabilità finite di avere risultati in corrispondenza dei valori 1, 2,…,6.
% stima distribuzione di probabilità di v.a. discreta
n = 1e5;
X = round(6*rand(n,1) + 0.5);
% lancio di un dado
xi = linspace(-2, 10, 3001);
FX = zeros(size(xi));
for k=1:length(xi)
FX(k) = sum(X<=xi(k))/n;
end
plot(xi,FX,'.')
xlabel('\xi')
ylabel('F_X(\xi)')
grid on
ylim([0 1.1])
Figura 1-10. Codice Matlab per stima distribuzione di probabilità: esempio variabile aleatoria
discreta
1
FX()
0.8
0.6
0.4
0.2
0
-2
0
2
4
6
8
10
Figura 1-11. Distribuzione di probabilità dei risultati del lancio di un dado stimata mediante il
codice di Figura 1-10.
Esempio 1.9. Stima distribuzione di probabilità di una variabile aleatoria continua
Il codice riportato in Figura 1-12 stima la distribuzione di probabilità della variabile
aleatoria continua X, il cui spazio campionario è generato attraverso una trasformazione
non-lineare di numeri casuali Gaussiani u. Per ogni valore (k) dell’ascissa discretizzata, la
distribuzione di probabilità è ottenuta valutando la probabilità dell’evento X (k)
mediante la definizione frequentista. La Figura 1-13 mostra la distribuzione di probabilità
stimata.
15
%
n
u
X
stima CDF della variabile aleatoria X
= 1e5;
% numero esperimenti
= randn(n,1);
= u + 0.1*u.^2 + 0.05*u.^3;
% generazione spazio campionario per X
xi = linspace(-10, 10, 300); % definizione ascissa discretizzata
FX = zeros(size(xi));
for k=1:length(xi)
FX(k) = sum(X<=xi(k))/n;
end
plot(xi,FX)
xlabel('\xi')
ylabel('F_X(\xi)')
grid on
ylim([0 1.1])
Figura 1-12. Codice Matlab per stima distribuzione di probabilità
1
FX()
0.8
0.6
0.4
0.2
0
-10
-8
-6
-4
-2
0
2
4
6
8
10
Figura 1-13. Distibuzione di probabilità di una variabile aleatoria continua stimata mediante il
codice di Figura 1-12.
1.5.3 Funzione di probabilità (di una variabile aleatoria discreta)
Si consideri una variabile aleatoria discrete X che può assumere gli n valori discreti j (j = 1,…,n).
Si definisce funzione di probabilità di X la funzione:
PX j P X j
(1.18)
che definisce, la probabilità di realizzazione di ogni possibile valore j. La funzione di probabilità e
la distribuzione di probabilità sono legate dalla relazione:
PX j FX j FX j
FX
P
j
X
j
(1.19)
(1.20)
dove j- indica un numero reale minore, ma arbitrariamente vicino a j. La Figura 1-14 mostra la
funzione di probabilità e la corrispondente distribuzione di probabilità di una variabile aleatoria
discreta.
16
0.8
0.7
1
0.6
0.8
PX()
FX()
0.5
0.6
0.4
0.3
0.4
0.2
0.2
0.1
0
1
2
3
4
0
1
2
3
4
Figura 1-14. Funzione di probabilità e distribuzione di probabilità di una variabile discrete.
Esempio 1.10. Stima della funzione di probabilità
Si consideri un esperimento realizzando lanciando due dadi. Sia X ottenuto come somma
dei risultati forniti dai due dati. La Figura 1-15 riporta il codice per simulare il lancio di due
dadi; la funzione di probabilità è valutata attraverso la funzione riportata in Figura 1-15
realizzata introducendo la definizione frequentista di probabilità nella (1.18).
La Figura 1-17 mostra la funzione di probabilità (a) e la distribuzione di probabilità (b)
stimata sulla base di 105 lanci di dadi simulati.
% esempio lancio di due dadi
n = 1e5;
X1 = round(6*rand(n,1) + 0.5);
X2 = round(6*rand(n,1) + 0.5);
X = X1 + X2;
% lancio di un dado 1
% lancio di un dado 2
[PX, xi] = pf1(X);
figure(1)
for k=1:length(xi)
plot(xi(k)*[1 1],PX(k)*[0 1],'b',xi(k),P(k),'.b')
hold on
end
hold off
xlim([0 14])
grid on
xlabel('\xi')
ylabel('P_X(\xi)')
Figura 1-15. Codice Matlab per simulazione del lancio di due dadi.
function [P, xi] = pf1(x)
% stima funzione di probabilità per v.a. discreta X di cui sono disponibili
% n realizzazioni contenute nel vettore x
% P = funxione di probabilità
% xi = ascissa P
xi = min(x):max(x);
% ascissa funz di probabilità
P = zeros(length(xi),1);
z = x - min(x) + 1;
for k=1:length(x)
P(z(k)) = P(z(k)) + 1;
end
P = P / length(x);
end
Figura 1-16. Codice Matlab per stima dai dati della funzione di probabilità di una variabile
aleatoria discreta.
17
0.18
1
0.16
0.14
0.8
0.1
FX()
PX()
0.12
0.08
0.6
0.4
0.06
0.04
0.2
0.02
0
0
2
4
6
8
10
12
0
14
0
2
4
6
8
10
12
(a)
14
(b)
Figura 1-17. Funzione di probabilità (a) e distribuzione di probabilità (b).
1.5.4 Densità di probabilità (di una variabile aleatoria continua)
La distribuzione di probabilità, FX, di una variabile aleatoria continua, X, è una funzione continua in
, ma non necessariamente derivabile. Si assuma che i punti in cui FX non è derivabile formino un
insieme numerabile. Ove FX è derivabile, si definisce la densità di probabilità pX() (o probability
density function, o pdf) come derivata di FX rispetto all’argomento :
pX
d FX
d
(1.21)
In virtù delle proprietà di FX si deducono le seguenti proprietà della densità di probabilità:
pX 0
(1.22)
FX pX d
(1.23)
pX d 1
2
P 1 X 2 FX 2 FX 1 pX d
1
(1.24)
1 2
(1.25)
In cui si è supposto che, nei punti dove pX non è definita (FX non derivabile), essa assuma un
qualsiasi valore positivo finito.
La Figura 1-18 descrive la relazione fra pX e FX definita dalla (1.23): l’ordinata FX() equivale
all’area sottesa da pX a sinistra dell’ascissa .
La Figura 1-19 mostra che l’occorrenza di un punto * in cui FX non è derivabile si riflette in una
discontinuità in pX.
18
(a)
(b)
Figura 1-18. Relazione fra densità (a) e distribuzione (b) di probabilità.
Figura 1-19. Punti singolari nella densità di probabilità.
La (1.25) afferma che l’area sottesa dalla densità di probabilità, compresa fra due valori di ascissa,
1 e 2, rappresenta la probabilità che la variabile aleatoria assuma un valore compreso in tale
intervallo (Figura 1-20). Ponendo 1 = e 2 = + , la (1.25) può essere riscritta nella forma:
P X
pX d
p X
(1.26)
Nella quale, l’applicazione del teorema della media impone di assumere che pX sia continua in .
Figura 1-20. Significato probabilistico di densità e distribuzione di probabilità.
19
L’applicazione della definizione empirica di probabilità alla (1.26) fornisce uno strumento per
stimare la densità di probabilità attraverso la relazione:
n
n n
pX lim
(1.27)
dove n() è il numero di volte in cui il valore di X è compreso nell’intervallo (, + ] in n
esperimenti. La densità così ottenuta è rappresentata da un istogramma (Figura 1-21) che, se è
sufficientemente piccolo può essere interpretato come la discretizzazione di una funzione di
variabile continua.
Figura 1-21. Stima della densità di probabilità.
Esempio 1.11. Stima della densità di probabilità.
Si consideri la variabile aleatoria del precedente Esempio 1.9 e si stimi la densità di
probabilità utilizzando la definizione frequentista.
%
n
u
X
stima pdf della variabile aleatoria X
= 1e6;
% numero esperimenti
= randn(n,1);
= u + 0.1*u.^2 + 0.05*u.^3;
% generazione spazio campionario per X
xi = linspace(-10, 10, 300); % definizione ascissa discretizzata
pX = zeros(size(xi));
Dx = xi(2) - xi(1);
for k=1:length(xi)
pX(k) = sum(X > xi(k)-Dx/2 & X <= xi(k)+Dx/2)/n/Dx;
end
plot(xi,pX)
xlabel('\xi')
ylabel('p_X(\xi)')
grid on
xlim([-6 6])
Figura 1-22. Codice Matlab per stima densità di probabilità.
20
0.45
0.4
0.35
pX()
0.3
0.25
0.2
0.15
0.1
0.05
0
-6
-4
-2
0
2
4
6
Figura 1-23. Densità di probabilità stimata mediante il codice riportato in Figura 1-22.
Il codice riportato in Figura 1-22 è molto semplice perché implementa brutalmente
l’estimatore definito dalla (1.27). Sfortunatamente, tale algoritmo è piuttosto inefficiente,
avendo una complessità computazionale pari a n2. In alternativa, la densità di probabilità
può essere stimata mediante la funzione riportata in Figura 1-24, che ha complessità
computazionale pari a n.
function [p, xi] = pdf1(x,Nx)
% stima pdf per v.a. continua X di cui sono disponibili le realizzazioni
% raccolte nel vettore x
% p = pdf
% xi = ascissa pdf
% Nx = numero punti ascissa pdf
xi = linspace(min(x),max(x),Nx)';
Dx = (max(x)-min(x)) / Nx;
% ascissa discretizzata pdf
% ampiezza intervalli
p = zeros(Nx,1);
z = (x - min(x)) / (max(x) - min(x));
z1 = round((Nx-1) * z)+1;
for k=1:length(x)
p(z1(k)) = p(z1(k)) + 1;
end
p = p / length(x) / Dx;
end
% x è mappato in [0 1]
% numero d'ordine intervallo ascissa
% normalizzazione
Figura 1-24. Codice Matlab per stima distribuzione di probabilità.
1.5.5 Valore atteso
Il valore atteso (o media, o expectation) di una variabile aleatoria X, è un numero E[X] che
formalizza l'idea euristica di valore medio di un fenomeno aleatorio.
In generale il valore atteso di una variabile aleatoria discreta è dato dalla somma dei possibili valori
di tale variabile, ciascuno moltiplicato per la probabilità di essere assunto (ossia di verificarsi), cioè
è la media ponderata dei possibili risultati. Se la variabile aleatoria X può assumere i valori j (j =
1,2,…), il valore atteso è definito dalla relazione:
E X j PX j
(1.28)
j 1
21
Per una variabile aleatoria continua il valore atteso è essere definito mediante un integrale.
E X
dFX
p d
X
(1.29)
Si osservi che la definizione di valore atteso ottenuta attraverso l’integrale di Stieltjes nella (1.29)
può essere applicata anche nei casi in cui la funzione densità di probabilità non è definita, come per
le variabili aleatorie discrete e miste.
Il valore atteso è un operatore lineare che dallo spazio delle variabili aleatorie conduce nello spazio
dei numeri reali. Esso gode quindi delle proprietà:
E aX bY a E X b E Y
(1.30)
dove X e Y sono variabili aleatorie, mentre a e b sono costanti reali.
Il valore atteso ha la proprietà di monotonia, cioè se una variabile aleatoria X appartiene
all’intervallo [a, b], allora anche il suo valore atteso E[X] appartiene ad [a, b].
Il valore atteso di una variabile aleatoria di cui è disponibile un insieme di realizzazioni può essere
stimato attraverso la media statistica. Ciò può essere dimostrato facilmente nel caso di variabili
aleatorie discrete (il concetto è altrettanto valido per le variabili continue) sostituendo la definizione
frequentista di probabilità nella (1.28)
E X
j 1
nj
j
(1.31)
n
dove nj rappresenta il numero di volte che si è realizzato il valore j nel corso di n esperimenti, con
n grande a sufficienza. La (1.31) contiene la somma dei risultati possibili j moltiplicati per il
numero di volte che questi si sono realizzati nj. Questa somma corrisponde alla somma dei valori xk
realizzati dalla variabile aleatoria negli n esperimenti (ammesso che n sia grande a sufficienza a fin
che l’insieme dei risultati xk contenga tutti i risultati j aventi una probabilità di occorrenza
significativa). La (1.31) può dunque essere riscritta nella forma:
E X
1 n
xk
n k 1
(1.32)
Il concetto di valore atteso può essere esteso al caso di una variabile aleatoria Y legata, attraverso
una funzione deterministica, ad una variabile aleatoria X di cui è nota la densità di probabilità (cioè,
Y = f(X), con f funzione deterministica). Il valore atteso di Y è fornito dalle espressioni:
E Y E f X f j PX j
(1.33)
j 1
E Y E f X
f p d
X
(1.34)
per i casi di variabili aleatorie discrete e continue, rispettivamente.
22
1.5.6 Momenti statistici di una variabile aleatoria
Si definisce momento statistico di ordine k (k ≥ 1) di una variabile aleatoria X il valore atteso della
potenza di ordine k di X:
mk X E X k
k 1, 2,
(1.35)
Sostituendo la (1.35) nelle (1.33) e (1.34), ponendo f(X) = Xk, si ottengono le espressioni:
mk X kj PX j
k 1, 2,
(1.36)
k 1, 2,
(1.37)
j 1
mk X
k
pX d
Il momento statistico di ordine 1, X = m1[X], è detto valore medio (o media); il momento statistico
di ordine 2, X2 = m2[X], è detto valore quadratico medio (o media quadratica).
Si definisce momento statistico centrale di ordine k (k ≥ 2) di una variabile aleatoria X la quantità:
k
k X E X X
k 2,3,
(1.38)
Il momento statistico centrale di ordine 2, X2 = 2[X] è detto varianza, mentre la sua radice
quadrata, X, è detta deviazione standard.
I momenti statistici centrali sono legati ai momenti statistici da relazioni ricorsive. Arrestandosi
all’ordine 4, risultano:
2 m2 m12
3 m3 3m 2 m1 2 m13
(1.39)
4 m4 4 m3 m1 6 m2 m12 3m14
Nel caso in cui X è una variabile aleatoria continua, la media X = m1[X] rappresenta, da un punto di
vista grafico, la posizione (ascissa) del baricentro dell’area sottesa dalla densità di probabilità;
pertanto, la media misura la posizione della funzione di densità di probabilità rispetto all’asse reale.
La media ha la medesima dimensione (unità di misura) delle realizzazioni della variabile aleatoria.
La varianza X2 = 2[X] rappresenta il momento d’inerzia dell’area sottesa dalla densità di
probabilità rispetto all’asse baricentrico; pertanto, la varianza rappresenta una misura di dispersione,
intono al valore medio, delle realizzazioni di una variabile aleatoria. La deviazione standard ha la
medesima dimensione delle realizzazioni della variabile aleatoria.
In accordo con le (1.39), media, varianza e media quadratica sono legate dalla relazione:
2X 2X 2X
(1.40)
Il rapporto fra deviazione standard e media è detto coefficiente di variazione:
IX
X
X
(1.41)
23
Il momento centrale di ordine 3, adimensionalizzato con la deviazione standard è detto skewness (o
coefficiente di asimmetria). Il momento centrale di ordine 4 adimensionalizzato con la deviazione
standard è detto kurtosis (o coefficiente di piattezza).
skw X
3 X
;
3X
kurt X
4 X
4X
(1.42)
Lo skewness è generalmente indicato con il simbolo 3. Frequentemente, al valore del kurtosis
definito dalla (1.42) si sottrae 3; in questo caso modo si ottiene un valore detto coefficiente di
eccesso (o eccesso di kurtosis), generalmente indicato con il simbolo 4.
3 X
3 X
;
3X
4 X
4 X
3
4X
(1.43)
La Figura 1-25 mostra l’effetto della media e della deviazione standard sulla forma della densità di
probabilità. La media determina una traslazione della curva lungo l’asse delle ascisse, mentre la
deviazione standard controlla l’ampiezza della curva (alla quale corrisponde un abbassamento per
conservare l’area unitaria).
La Figura 1-26 mostra l’effetto di skewness e coefficiente di eccesso sulla forma della densità di
probabilità. La condizione 3 = 0 corrisponde ad una funzione simmetrica rispetto alla media; la
condizione 3 > 0 rappresenta la situazione in cui la densità di probabilità ha la coda di destra più
alta della coda di sinistra. Una variabile aleatoria avente 4 > 0 è detta supergaussiana e ha densità di
probabilità alta sulla moda (ascissa corrispondente al picco) e sulle code; una variabile aleatoria
avente 4 < 0 è detta subgaussiana e ha densità di probabilità bassa sulla moda e sulle code; il caso
4=0 corrisponde alla distribuzione Gaussiana che verrà descritta nel seguito. Per lo studio delle
code della distribuzione è generalmente conveniente diagrammare le funzioni di densità di
probabilità con ordinata in scala logaritmica, come mostrato in Figura 1-27 per i casi già discussi in
Figura 1-26.
È possibile dimostrare che il coefficiente di eccesso è inferiormente limitato a 4 = -2; tale valore è
attinto da variabili aleatorie con densità del tipo:
pX
1
1 1
2
(1.44)
Una variabile aleatoria è detta standardizzata se è centrata rispetto alla sua media e scalata in modo
da avere varianza unitaria:
X X
Xˆ
X
(1.45)
da cui ovviamente risulta Xˆ 0 e Xˆ 1 .
24
0.4
0.4
X = 0
X = 1
X = 0
X = 1
0.35
0.3
0.25
0.25
Y
p (), p ()
0.3
Y
p (), p ()
0.35
Y = 1
Y = 1
0.2
X
X
0.2
0.15
0.15
0.1
0.1
0.05
0.05
0
-4
-3
-2
-1
0
,
1
2
3
Y = 0
Y = 2
0
-6
4
-4
-2
0
,
(a)
2
4
6
(b)
Figura 1-25. Densità di probabilità: influenza della media (a) e deviazione standard (b).
0.45
3 = 0.5
4 = 0
0.4
0.7
3 = -0.5
4 = 0
3 = 0
4 = 5
0.6
3 = 0
4 = 0
Z
0.4
Y
0.25
Y
0.2
3 = 0
4 = -0.5
0.3
X
X
3 = 0
4 = 0
0.5
p (), p (), p ()
0.3
Z
p (), p (), p ()
0.35
0.15
0.2
0.1
0.1
0.05
0
-4
-3
-2
-1
0
, ,
1
2
3
0
-4
4
-3
-2
-1
(a)
0
, ,
1
2
3
4
(b)
0
10
0
10
-1
10
-1
10
-2
10
-2
10
-3
10
-3
Y
-4
X
X
Y
Z
p (), p (), p ()
10
Z
p (), p (), p ()
Figura 1-26. Densità di probabilità: influenza skewness (a) e coefficiente di eccesso (b).
-3
-2
-1
0
, ,
1
2
3
4
-4
-3
(a)
-2
-1
0
, ,
1
2
3
4
(b)
Figura 1-27. Densità di probabilità (scala logaritmica): influenza skewness (a) e coefficiente di eccesso (b).
I momenti statistici della variabile aleatoria X possono essere stimati a partire da un insieme di sue
realizzazioni xj (j = 1,…,n) attraverso un’espressione analoga alla (1.32)
mk X E X k
1 n k
xj
n j 1
(1.46)
25
1.5.7 Funzione caratteristica di una variabile aleatoria continua
Si definisce funzione caratteristica (o funzione generatrice dei momenti) della variabile aleatoria X,
la funzione a valori complessi:
X E exp i X ei pX d
(1.47)
dove l’argomento è definito in ℝ. In base alla (1.47), la funzione caratteristica è la trasformata di
Fourier della densità di probabilità, pertanto essa determina completamente la struttura
probabilistica di X.
La funzione caratteristica può essere rappresentata attraverso la serie di McLaurin:
1 dk X
k
k 1 k ! d
X X 0
k
(1.48)
0
Operando per derivazione sulla (1.47), i termini della (1.48) risultano nella forma:
X 0 1
dk
i k E X k i k mk X
k
d 0
k 1, 2,
(1.49)
che, sostituendo nella (1.48), forniscono un’espressione della funzione caratteristica in termini di
momenti statistici.
ik
m k X k
k 1 k !
X 1
(1.50)
La (1.50) dimostra che, conoscendo i momenti statistici fino all’ordine infinito, è possibile
rappresentare la funzione caratteristica e quindi la densità di probabilità. In questo senso, la
conoscenza dei momenti statistici è equivalente alla conoscenza della distribuzione di probabilità,
quindi determina completamente la struttura probabilistica della variabile aleatoria.
1.5.8 Cumulanti
Si definisce log-funzione caratteristica ΨX(θ) della variabile aleatoria X il logaritmo naturale della
funzione caratteristica ΦX(θ); tale funzione può essere espansa attraverso la serie di McLaurin come
segue:
X log X
j 1
1 d j X
j! d j
j
0
i
j X
j!
j 1
j
(1.51)
i cui coefficienti κj[X] sono detti cumulanti. I cumulanti sono legati ai momenti statistici ed ai
momenti centrali attraverso le relazioni ricorsive riportate in appendice A; tali relazioni, fino
all'ordine 4, hanno la forma:
26
1 m1
2 m 2 m12 2
(1.52)
3 m3 3m 2 m1 2 m12 3
4 m 4 3m 2 2 4 m3 m1 12 m 2 m12 6 m14 4 3 22
Si osserva che il quarto cumulante adimensionalizzato rispetto alla deviazione standard corrisponde
al coefficiente di eccesso definito in (1.43).
1.5.9 Entropia
Sia X una variabile aleatoria discreta con funzione di probabilità PX(ξj). Si definisce entropia (di
Shannon) la quantità:
H X PX j log PX j
(1.53)
j
dove la sommatoria è estesa a tutti i valori ξj che X può assumere. Considerando la funzione
f p p log p diagrammata in Figura 1-28, l'entropia può essere generalizzata nella forma:
H X f PX j
(1.54)
f(p)
j
0
0.2
0.4
0.6
0.8
1
p
Figura 1-28. Funzione f(p) nell'intervallo [0,1]
Dalla (1.54) si osserva che H è un numero non negativo ed è nullo nel caso in cui X sia
deterministica (un particolare ξj ha probabilità uno e tutti gli altri hanno probabilità zero). In
generale H è piccola se un valore ξj ha una probabilità di occorrenza dominante, mentre H è grande
se molti valori ξj hanno probabilità di occorrenza comparabile.
In termini qualitativi, l'entropia misura il grado di "aleatorietà" di una variabile aleatoria o, in
termini più corretti, specifica quanto una variabile aleatoria è strutturata.
In teoria dell'informazione l'entropia è utilizzata per quantificare il contenuto di informazione di un
canale digitale.
Sia ora X una v.a. continua; si definisce entropia (differenziale) la quantità:
H X pX log pX d
(1.55)
27
dove l'integrazione è estesa all'intero dominio di definizione di pX. A differenza dell'entropia di
Shannon, l'entropia integrale può assumere valori negativi (dato che la funzione densità di
probabilità può essere maggiore di uno); da un punto di vista qualitativo possiede il medesimo
significato.
1.5.10 Trasformazioni lineari di variabili aleatorie
Sia X una variabile aleatoria continua e Y una sua trasformazione lineare tale che Y = aX + b con
a, b . Le rispettive distribuzioni di probabilità sono legate dalla relazione
b
b
FY PY Y PY aX b PX X
FX
a
a
(1.56)
Segue che le densità di probabilità sono legate dalla relazione
pY
dFY 1 dFX
1
b
pX
d
a d b a
a
(1.57)
a
Le funzioni caratteristiche di X e Y ed i loro logaritmi sono legate dalle relazioni
Y E exp i Y E exp i aX b
E exp i aX exp i b X a exp i b
Y log Y X a ib
(1.58)
(1.59)
Dalla (1.59) segue che i cumulanti delle due variabili aleatorie X e Y sono legati nel seguente modo
1 Y a1 X b
j Y a j j X
j2
(1.60)
Nel caso particolare in cui b = 0 la (1.60) vale anche per i momenti e assume la forma
m j aX a j m j X
j aX a j j X
(1.61)
La (1.61) dimostra che momenti e cumulanti di ordine j sono operatori omogenei di grado j.
Infine l'entropia di X e Y si relazionano nel seguente modo
H Y pY log pY d
1
X b 1
X b
pX
log p X
d
a
a a
a
(1.62)
1
p X log p X d
a
H X log a
28
da cui si deduce che l'entropia aumenta con la scala a ed è invariante rispetto alla posizione. In altri
termini, fissata la forma della distribuzione di probabilità, l'entropia cresce all'aumentare della
varianza ed è invariante rispetto al valor medio.
1.5.11 Trasformazioni non lineari di variabili aleatorie
Sia X una variabile aleatoria continua e Y = g(X) con g funzione monotona crescente. La funzione di
distribuzione FY può essere relazionata a FX imponendo che P Y sia pari a P X g 1
dove g-1 è la funzione inversa di g (Figura 1-29).
Figura 1-29.
Da questa uguaglianza discende la relazione:
FY FX g 1
(1.63)
che in termini di densità di probabilità risulta:
dFY dFX
dg 1
dg 1
1
pY
p X g
d
d g 1 d
d
(1.64)
Se la funzione g è monotona decrescente la relazione che lega FX e FY può essere ricavata
eguagliando P Y e P X g 1 (Figura 1-30).
Figura 1-30.
Da questa uguaglianza discendono le relazioni
29
FY 1 FX g 1
pY p X g 1
dg 1
d
(1.65)
Le (1.65) possono essere unificate per comprendere sia il caso di funzione crescente che
decrescente attraverso la relazione:
pY p X g 1
dg 1
d
(1.66)
Le entropie di X e Y sono legate dalla relazione
H Y pY log pY d
pX g
1
dg 1
dg 1
1
log p X g
d
d
d
dg 1
p X log p X
d
d
g
dg
H X p X log
d
(1.67)
d
L'integranda nella (1.67) fornisce un contributo positivo all'entropia per i valori di ξ per cui
dg d 1 , mentre fornisce un contributo negativo quando dg d 1 . Questo effetto è pesato
dalla densità di probabilità pX.
1.6 Modelli di variabili aleatorie
Nel presente capitolo si introducono alcuni modelli probabilistici rilevanti per lo studio della
meccanica delle vibrazioni e dell’affidabilità strutturale. Il modello normale (o Gaussiano) è
descritto con maggiore enfasi in virtù delle sue caratteristiche probabilistiche e della sua importanza
applicativa.
1.6.1 Distribuzione normale (o Gaussiana)
Una variabile aleatoria X ha distribuzione normale (o Gaussiana) se la sua densità di probabilità è
nella forma:
2
1
1 X
pX
exp
2 X
2 X
(1.68)
Una variabile aleatoria X, con distribuzione normale X e varianza X2 è formalmente definita
attraverso l’espressione X = N(X, X2). La Figura 1-31 mostra la densità di probabilità di una
variabile aleatoria normale standardizzata; nel piano semilogaritmico la curva è costituita da una
parabola.
30
0
0.4
10
0.35
-1
0.3
10
pX()
pX()
0.25
0.2
-2
10
0.15
-3
0.1
10
0.05
0
-4
-4
-3
-2
-1
0
1
2
3
10
4
-4
-3
-2
-1
0
(a)
1
2
3
4
(b)
Figura 1-31. Densità di probabilità normale: ordinata in scala decimale (a) e logaritmica (b).
La distribuzione di probabilità è data dall’espressione:
1
FX
2 X
1 2
exp 2 X X d
(1.69)
che può essere scritta in forma analitica attraverso la funzione di errore
X
1
FX 1 erf
2
X
(1.70)
Per ispezione della (1.68) è immediato verificare che se Y = aX + b, con a e b costanti
deterministiche e X = N(X, X2), allora Y = N(aX + b, a2X2).
La funzione caratteristica di una variabile Gaussiana può essere ottenuta calcolando la trasformata
di Fourier della (1.68) e risulta:
1
X exp i X 2X 2
2
(1.71)
Se X è una variabile aleatoria Gaussiana standardizzata, X = N(0,1), allora densità di probabilità e
distribuzione di probabilità risultano:
1
1
exp 2
2
2
2
1
1
FX
exp
d 1 erf
2
2
2
1
X exp 2
2
pX
(1.72)
(1.73)
(1.74)
Si osserva che la funzione caratteristica di una variabile Gaussiana standardizzata è formalmente
identica alla corrispondente funzione densità di probabilità.
1.6.2 Distribuzione uniforme
Una variabile aleatoria continua ha distribuzione uniforme se la sua densità di probabilità è espresso
nella forma:
31
1/ b a
pX
0
per a b
altrove
a b
(1.75)
Il modello uniforme è utilizzato quando una variabile aleatoria può assumere valori equiprobabili in
un intervallo chiuso [a, b]. La funzione di distribuzione può essere ottenuta dalla (1.75) per
integrazione e risulta:
per a
per a b
0
FX a / b a
1
(1.76)
per b
La media e la varianza di una variabile aleatoria uniforme risultano:
X a b / 2
(1.77)
2X b a /12
(1.78)
FX()
pX()
2
1/(b-a)
0
0
a
1
0
b
0
a
b
Figura 1-32. Densità e distribuzione di probabilità di una variabile aleatoria uniforme.
1.6.3 Modello log-normale
Una variabile aleatoria X è della log-normale se Y = log(X) ha distribuzione normale. La densità di
probabilità di una variabile log-normale è espressa nella forma:
log m 2
1
pX
exp
2
2
s
2 s
(1.79)
dove m e s sono i parametri della distribuzione (e rappresentano, rispettivamente, la media e la
deviazione standard di Y). La media e la varianza di X risultano:
s2
X exp m
2
exp 2m s exp s 1
2
X
2
(1.80)
2
32
0.25
1
0.9
0.2
0.8
0.7
0.6
pX()
FX()
0.15
0.1
0.5
0.4
0.3
0.05
0.2
0.1
0
0
2
4
6
8
10
12
14
16
18
0
20
0
2
4
6
8
10
12
14
16
18
20
Figura 1-33. Densità e distribuzione di probabilità di una variabile aleatoria log-normale (m = 1, s = 1).
1.6.4 Modello di Rayleigh
Una variabile aleatoria X è detta di Rayleigh se ha densità di probabilità nella forma:
pX
2
exp
2
b2
2b
(1.81)
dove b è il parametro della distribuzione.
0.7
1
0.9
0.6
0.8
0.5
0.7
0.6
pX()
FX()
0.4
0.3
0.5
0.4
0.3
0.2
0.2
0.1
0.1
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
0
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Figura 1-34. Densità e distribuzione di probabilità di una variabile aleatoria di Rayleigh (b = 1).
1.6.5 Modello di binomiale
Si consideri una successione di variabili aleatorie discrete, Xk (k = 1,2,…), aventi spazio
campionario Ω = {0, 1}. Si assuma che gli eventi legati a ogni possibile coppia di variabili aleatorie
Xh e Xk (h,k = 1,2,…; hk) siano statisticamente indipendenti; sia inoltre P(Xk = 1) = p.
La successione Xk è detta sequenza di Bernoulli. La funzione di probabilità di una variabile aleatoria
di Bernoulli risulta dunque:
PX k 0 P X k 0 1 p
PX k 1 P X k 1 p
(1.82)
Sia Ym una variabile aleatoria discreta definita come la somma dei primi m termini di una sequenza
di Bernoulli (Figura 1-35):
33
m
Ym X k
(1.83)
k 1
9
8
7
Xk, Yk
6
5
4
3
2
1
0
0
5
10
15
k
20
25
30
Figura 1-35. Sequenza di Bernoulli (blu) e corrispondente sequenza binomiale (rosso).
La funzione di probabilità di Ym può essere ottenuta operando in modo ricorsivo. Per m=1, la
funzione di probabilità di Ym = Y1 risulta:
PY1 0 P Y1 0 P X 1 0 1 p
PY1 1 P Y1 1 P X 1 1 p
(1.84)
Analogamente, per m=2, la funzione di probabilità di Ym = Y2 risulta (per il teorema dell’evento
totale e per l’ipotesi di indipendenza statistica fra le variabili di Bernoulli):
PY2 0 P Y2 0 P X 1 0 X 2 0 1 p
2
PY2 1 P Y2 1 P X 1 1 X 2 0 X 1 0 X 2 1 2 p 1 p
(1.85)
PY2 2 P Y2 2 P X 1 1 X 2 1 p 2
Le (1.84) e (1.85) possono essere generalizzate, per un m qualsiasi in , attraverso l’espressione:
m
m
PYm P Ym p 1 p
(1.86)
dove il binomio di Newton è espresso nella forma:
m
m!
! m !
(1.87)
Sostituendo la (1.86) nell’espressione di media e varianza risulta:
Ym mp
Y2m mp 1 p
(1.88)
34
da cui si evince che la media e la varianza di una variabile binomiale sono lineari in m.
Esempio 1.12. Sequenze di Bernoulli e variabili binomiali
Il codice riportato in Figura 1-36 simula una serie di sequenze di Bernoulli di lunghezza n e
la variabile Binomiale Ym ottenuta per m = n. La stima di media (Figura 1-37a), varianza
(Figura 1-37b) e funzione di probabilità (Figura 1-38) è effettuata applicando la definizione
frequentista di probabilità. I risultati della stima sono confrontati con quanto previsto dal
modello binomiale.
Nseq = 10000;
% numero realizzazioni
n = 30;
p = 0.2;
% numero esperimenti di Bernoulli
% prob. di successo esperimenti di Bernoulli
X = rand(n,Nseq) >= (1-p);
Y = cumsum(X);
% sequenza di Bernoulli
% sequenza binomiale
m = n;
% considero m = n esperimenti
% stima funzione di probabilità dai dati
[PY_data, eta_data] = pf1(Y(m,:));
% modello binomiale
eta = 0:m;
% ascissa per PY
PY_bi = factorial(m)./factorial(eta)./factorial(m-eta) .* (p.^eta) .* ((1p).^(m-eta));
figure(1)
plot(1:n,mean(Y,2),'--.b', 1:n,(1:n)*p,'-r')
xlabel('m')
ylabel('\mu_{Y_m}')
figure(2)
plot(1:n,var(Y,[],2),'--.b', 1:n,(1:n)*(1-p)*p,'-r')
xlabel('m')
ylabel('\sigma^2_{Y_m}')
figure(3)
bar(eta_data,PY_data)
hold on
plot(eta, PY_bi,'-*r')
hold off
xlabel('\eta')
ylabel('p_{Y_m(\eta)}')
xlim([0 20])
Figura 1-36. Codice Matlab per simulazione di sequenze di Bernoulli e binomiali; stima di
media, varianza e funzione di probabilità della variabile binomiale.
6
5
4.5
5
4
3.5
4
m
2Y
Y
m
3
3
2.5
2
2
1.5
1
1
0.5
0
0
5
10
15
m
20
25
0
30
(a)
0
5
10
15
m
20
25
30
(b)
Figura 1-37. Media (a) e varianza (b) della variabile binomiale simulata nel codice di Figura
1-36: stima dai dati (blu), modello (rosso).
35
0.2
0.18
0.16
0.14
pY ()
m
0.12
0.1
0.08
0.06
0.04
0.02
0
0
2
4
6
8
10
12
14
16
18
20
Figura 1-38. Funzione di probabilità della variabile binomiale simulata nel codice di Figura
1-36: stima dai dati (blu), modello (rosso).
1.6.6 Modello di Poisson
Una variabile aleatoria discrete Y ha distribuzione di Poisson se la sua funzione di probabilità è
nella forma:
PY
exp
!
0,1,
(1.89)
Dalla (1.89) risulta, evidentemente, che PY(0) = e-; inoltre Y = Y2 = . Al variare del parametro ,
la funzione di probabilità assume le forme mostrate in Figura 1-39.
0.5
0.45
= 0.7
0.4
0.35
PY ()
0.3
= 2.5
0.25
0.2
= 5.0
0.15
0.1
0.05
0
0
2
4
6
8
10
12
Figura 1-39. Funzione di probabilità di una variabile di Poisson al variare del parametro .
Una variabile aleatoria di Poisson, Y, può essere interpretata come il limite, per m , di una
sequenza binomiale Ym derivata da una sequenza di Bernoulli Xk avente probabilità di successo
p0. In tal caso la variabile Y è definita dal parametro = mp.
36
La Figura 1-39 mostra la funzione di probabilità di tre variabili aleatorie binomiali definite,
rispettivamente, dai parametri m = 10, 20 e 100 e p = 0.50, 0.25, 0.05 (blu) e di una variabile
aleatoria di Poisson definita dal parametro = 5.
0.25
m = 10
PYm(), P Y ()
0.2
m = 20
m = 100
0.15
0.1
0.05
0
0
1
2
3
4
5
6
7
8
9
10
Figura 1-40. Convergenza di variabili binomiali (blu) a una variabile di Poisson (rosso).
1.7 Rappresentazioni approssimate della densità di probabilità
Si affronta il problema di definire un'approssimazione della densità di probabilità di una variabile
aleatoria sulla base di limitate informazioni sintetiche, come ad esempio un numero finito di
momenti statistici e cumulanti.
1.7.1 Espansione in serie di funzioni ortogonali
Sia X una variabile aleatoria continua e X la sua versione standardizzata; pX e pX sono le
rispettive densità di probabilità. Sia inoltre pG la densità di probabilità di una variabile
Gaussiana standardizzata, ovvero
1 2
pG
e
2
2
(1.90)
Se pX ha le code sufficientemente basse (è sufficiente che pX
serie di funzioni ortogonali è uniformemente convergente in :
pX
pG
a j j
(1.91)
j 0
dove Ψj son un insieme di funzioni ortogonali in
j
pG L2 ), allora la seguente
che può essere definito come segue:
1
H j pG
j!
(1.92)
in cui Hj(ξ) sono polinomi di Hermite (Appendice B).
Le funzioni definite in (1.92) sono ortonormali in
, cioè:
d
j
k
jk
(1.93)
37
Sfruttando la (1.93), i coefficienti aj della serie (1.91) possono essere valutati attraverso la
relazione:
aj
p Xˆ
pG
j d
1
pX H j d
j!
1
E H j Xˆ
j!
(1.94)
I coefficienti della serie (1.91) sono proporzionali al valore atteso dei polinomi di Hermite in X̂ .
Sostituendo la (1.92) e la (1.94) nella (1.91), pX̂ assume la forma:
1
pXˆ pG b j H j
j 1 j !
(1.95)
dove i coefficienti
bj
j ! a j E H j Xˆ
(1.96)
sono detti momenti di Hermite o quasi-momenti.
I primi momenti di Hermite hanno la forma:
b0 1
b1 E Xˆ 0
b2 E Xˆ 2 1 0
(1.97)
b3 E Xˆ 3 3 Xˆ 3 Xˆ 3 X
b4 E Xˆ 4 6 Xˆ 2 3 4 Xˆ 4 X
In generale i momenti di Hermite sono legati ai cumulanti dalla relazione ricorsiva:
j 1!
k j r br
r 3 r ! j r 1 !
j 3
bj k j
(1.98)
Nota la densità di probabilità della variabile standardizzata X̂ , pX(ξ) può essere calcolata attraverso
la (1.57)
pG
1
pX
bj H j
j 1 j !
(1.99)
dove μ e σ sono la media e la deviazione standard di X. La (1.99) è chiamata serie di Gram-Charlier
tipo A.
1.7.2 Principio di massima entropia
Si suppongo di conoscere la variabile aleatoria X attraverso le grandezze
38
c j pX Fj d E Fj X
j 1,..., n
(1.100)
dove Fj sono funzioni arbitrarie tali da far convergere l'integrale nella (1.100). La conoscenza di un
numero finito di cj non permette di stimare il valore esatto di pX . Tuttavia se p0(ξ) è la densità
di probabilità compatibile con il vincolo (1.100) che massimizza l'entropia di X, allora p0
rappresenta la v.a. compatibile con i vincoli meno strutturata possibile. In altre parole, il principio di
massima entropia fornisce una densità di probabilità, compatibile con i dati, facendo meno
assunzioni possibili sulla sua struttura. La densità di probabilità che soddisfa il principio di massima
entropia è nella forma:
n
p0 A exp a j Fj
j 0
(1.101)
dove A e aj sono costanti determinate imponendo le (1.100) e la condizione di normalizzazione.
Se si sceglie Fj(ξ) = Hj(ξ), la (1.101) riscritta per la variabile standardizzata X̂ , è chiamata serie di
Gram-Charler tipo C e assume la forma
n
pXˆ A exp j H j
j 0
(1.102)
dove γj sono costanti da determinare. A tale scopo, si considera una funzione f(ξ) che cresce per
|ξ|→∞ più lentamente di un'esponenziale. Sotto questa ipotesi sussiste la relazione
f dpXˆ
p df 0
Xˆ
(1.103)
che può essere facilmente dimostrata attraverso la formula di integrazione per parti. Scegliendo
f Hi 1 , sostituendo la (1.102) nella (1.103) e sfruttando le proprietà dei polinomi di
Hermite (Appendice B) risulta:
n
j
j 1
j
H i 1 H j 1 pXˆ d i 1 H i 2 p Xˆ d 0
(1.104)
È possibile dimostrare che il prodotto di polinomi di Hermite nel primo integrale può essere
espresso nella forma:
H i 1 H j 1
i j 2
1
k! A
k 0
i 1, j 1, k
Hk
(1.105)
dove
Ap ,q ,k
1
se p q k pari e p, q, k
p ,q ,k 1
0
altrimenti
(1.106)
in cui p q k 2 .
39
Sostituendo la (1.105) nella (1.104) si ottengono le relazioni:
i j 2 1
j
Ai 1, j 1,k bk i 1 bi 2 0
j
j 1
k 0 k !
n
i 1, 2,..., n
(1.107)
dove bj sono i momenti di Hermite di X̂ . La (1.107) rappresenta un sistema di n equazioni lineari
nei coefficienti γj (j = 1,…,n) la cui valutazione richiede la conoscenza dei momenti di Hermite fino
all'ordine 2n-2. Una volta calcolati i coefficienti γj (j = 1,…,n) risolvendo le (1.107) la densità di
probabilità di X è ottenuta nella forma:
pX
e 0
n
exp j H j
j 1
(1.108)
dove γ0 è ottenuto imponendo la condizione di normalizzazione.
1.7.3 Trasformazione non-lineare di variabili Gaussiane
Sia X una variabile aleatoria continua di cui sono noti i momenti di Hermite fino all'ordine n+1. La
corrispondente v.a. standardizzata X̂ è approssimata attraverso l'espressione:
n
Xˆ a j H j U
(1.109)
j 0
dove U è una variabile Gaussiana standard.
I coefficienti della sommatoria sono calcolati imponendo l'uguaglianza dei momenti di Hermite dei
due membri della (1.109) fino all'ordine n+1
n
E H k Xˆ E H k a j H j U
j 0
n 1,..., n 1
(1.110)
Svolgendo i prodotti impliciti nel membro di destra della (1.110) si ottengono polinomi in U fino al
grado nk nella forma:
nk
bk jk
j 0
nk
j 0
j dispari
m j U
E U j
j!
jk
i 2
j 2 !2
k 1,..., n 1
(1.111)
In cui si è impiegata la formula che fornisce i momenti statistici di prodotti di variabili aleatorie
Gaussiane (Appendice E). I coefficienti αj(k) sono legati ai coefficienti aj da relazioni polinomiali
piuttosto complesse.
Nel caso particolare n = 3 le (1.111) assumono la forma esplicita:
40
b1 0 a0
b2 0 a12 2a22 6a32 1
b3 3 X 2a2 3a12 18a1a3 4a22 54a32
(1.112)
b4 4 X 3a14 24a13a3 60a12 a22 252a12 a32 6a12
576a1a22 a3 1296a1a33 60a24 2232a22 a32
12a22 3348a34 36a32 3
I coefficienti a0 - a3 possono essere calcolati attraverso le (1.112) dati skewness e coefficiente di
eccesso.
La densità di probabilità di X̂ è ottenuta applicando la (1.66):
1
2 dg
1
1
exp g 1
2
d
2
pXˆ
(1.113)
Nel caso n = 3, la funzione g-1 e la sua derivata prima possono essere ottenute in forma chiusa:
1
1
3
3
2
2
g cH cH a H
1
dg 1 bH
d
2a1
c
2
c
2
H
H
2
3
2
3
1
2 c
H
(1.114)
1
2 c
H
dove
aH
a2
3a3
bH
a1
3a3
cH bH 1 aH2
(1.115)
3
La densità di probabilità della variabile X è ottenuta a partire dalla (1.113) nella forma:
1
1
X
exp g 1
2
2 X
X
2
pX
X
dg 1
X
d
(1.116)
Il modello di densità di probabilità fornito dalle (1.114)-(1.116) è chiamato Moment-Based Hermite
Transformation (MBHT).
41
La Figura 1-41 mostra la densità di probabilità di una variabile aleatoria stimata a partire dai primi
quattro momenti di Hermite mediante i tre metodi sopra discussi. La densità Gaussiana è aggiunta
per confronto.
0
10
Dati
Gram-Charlier A
Gram-Charlier C
MBHT
Gaussiana
0.5
-1
10
-2
10
pX()
pX()
0.4
0.3
-4
0.2
10
Dati
Gram-Charlier A
Gram-Charlier C
MBHT
Gaussiana
-5
0.1
0
-3
-3
10
10
-6
-2
-1
0
1
2
3
10
-10
-8
-6
-4
-2
0
2
4
6
8
10
Figura 1-41. Densità di probabilità stimata mediante serie di Gram-Charlier A e C e mediante MBHT.
42
1.8 Rappresentazione della relazione probabilistica fra due grandezze
Nei paragrafi precedenti si è discusso su come rappresentare, probabilisticamente, variabili aleatorie
continue e discrete. In molte applicazioni è necessario rappresentare contemporaneamente più
variabili aleatorie e definirne le mutue relazioni statistiche che le governano. Ad esempio, ha senso
chiedersi quale sia la relazione statistica che intercorre il modulo elastico di un provino di acciaio e
la sua tensione si snervamento, oppure fra la velocità del vento (in un determinato luogo, ad un
certo istante) e la sua direzione.
Al fine di sviluppare strumenti per rappresentare la mutua relazione probabilistica fra diverse
grandezze, si considerino due variabili aleatorie, X e Y, con valori in . Per semplicità si assuma
che X e Y siano variabili aleatorie continue.
1.8.1 Distribuzione congiunta di probabilità
La distribuzione congiunta di probabilità, FXY(,), delle variabili aleatorie X e Y è, per definizione,
la probabilità che si verifichi l’evento X Y per la generica coppia di valori e in :
FXY , P X Y
(1.117)
In questo contesto, le distribuzioni di probabilità FX() e FY() delle variabili aleatorie X e Y
(considerate separatamente) sono chiamate distribuzioni marginali di probabilità. In generale, la
conoscenza delle distribuzioni marginali non è sufficiente a definire la distribuzione congiunta;
viceversa, nota la distribuzione congiunta, le marginali risultano:
FX P X Y FXY ,
FY P X Y FXY ,
(1.118)
La distribuzione congiunta di probabilità gode delle seguenti proprietà (dimostrabili facilmente
attraverso la definizione (1.117) e gli assiomi della teoria della probabilità):
FXY , P X Y P 0
FXY , P X Y P 0
FXY , P X Y P 0
(1.119)
FXY , P X Y P 1
Inoltre, con semplici passaggi è possibile dimostrare che FXY(,) è una funzione non-decrescente
di , :
FXY 2 , FXY 1 ,
FXY , 2 FXY , 1
2 1
2 1
(1.120)
cioè la distribuzione congiunta di probabilità è una funzione non-decrescente di e .
1.8.2 Densità congiunta di probabilità
Si consideri le variabili aleatorie X e Y definite dalla distribuzione congiunta di probabilità FXY(,),
supposta derivabile per ogni e in , salvo che, al più, in insiemi di misura nulla (punti o linee).
Si definisce densità di probabilità congiunta:
43
2 FXY ,
p XY ,
(1.121)
Per la (1.120), la densità di probabilità risulta non-negativa. La (1.121) può essere invertita
applicando il teorema fondamentale del calcolo integrale (in forma bi-dimensionale)
FXY ,
pXY , d d
(1.122)
per la quale il valore della distribuzione congiunta nel punto (, ) corrisponde al volume sotteso
dalla densità congiunta nel dominio definito dai punti (, ) con e .
1
0.015
0.01
XY
0.4
p
F
(,)
0.6
XY
(,)
0.8
0.005
0.2
0
10
0
10
10
10
5
0
-10
-5
-10
5
0
0
0
-10
(a)
-5
-10
(b)
Figura 1-42. Distribuzione congiunta (a) e densità congiunta (b) di probabilità di due variabili aleatorie continue.
Applicando il teorema dell’evento totale, è possibile dimostrare le relazioni (Figura 1-43):
P 1 X 2 1 Y 2 P X 2 Y 2 P X 1 Y 2
P X 2 Y 1 P X 1 Y 1
FXY 2 , 2 FXY 1 , 2 FXY 2 , 1 FXY 1 , 1 (1.123)
2
1
2
1
p XY , d d
2
1
1
2
Figura 1-43. Rappresentazione grafica dell’equazione (1.123).
44
Da cui discenda, per l’assioma di normalizzazione della probabilità:
pXY , d d 1
(1.124)
Riscrivendo la (1.123) per 1 = - e 2 = +, si ottiene, per definizione, la distribuzione marginale
di probabilità della variabile X
P 1 X 2 Y P 1 X 2 FX x
p XY , d d
(1.125)
la quale, derivata rispetto a fornisce la densità marginale di probabilità:
p X
pXY , d
(1.126)
Operando analogamente rispetto alla variabile , si ottiene la densità marginale di probabilità della
variabile aleatoria Y:
pY
pXY , d
(1.127)
In maniera equivalente, le variabili aleatorie X e Y possono essere rappresentate attraverso la
funzione caratteristica congiunta
XY , E exp i X i Y
e
i
p XY , d d
(1.128)
che corrisponde alla trasformata di Fourier bi-dimensionale della densità di probabilità congiunta.
Nota la funzione caratteristica congiunta, le funzioni caratteristiche marginali possono essere
ottenute annullando uno dei due argomenti della funzione:
X XY , 0
Y XY 0,
(1.129)
Si definisce log-funzione caratteristica congiunta il logaritmo naturale di XY
XY , log XY ,
(1.130)
1.8.3 Variabili aleatorie statisticamente indipendenti
Due eventi A e B sono definititi statisticamente indipendenti se la probabilità composta della loro
occorrenza è pari al prodotto della probabilità di occorrenza dei due eventi considerati
singolarmente (P(AB) = P(A)P(B)). Due variabile aleatorie X e Y si definiscono statisticamente
indipendenti se gli eventi {X } e {Y } sono statisticamente indipendenti. Da questa
definizione segue immediatamente che, X e Y sono statisticamente indipendenti se e solo se la
distribuzione (densità) congiunta di probabilità è pari al prodotto delle distribuzioni (densità)
marginali. Lo stesso vale per le funzioni caratteristiche.
45
FXY , FX FY
p XY , p X pY
(1.131)
XY , X Y
La log-funzione caratteristica di due variabili aleatorie statisticamente indipendenti è la somma
delle log-funzioni caratteristiche marginali
XY , X Y
(1.132)
1.8.4 Valore atteso
Nel paragrafo 1.5.5 si introduce il concetto di valore atteso, definito come la media di tutti i
possibili valori realizzabili da una variabile aleatoria X, pesati attraverso la loro probabilità di
occorrenza. Attraverso l’equazione (1.34) il concetto di valore atteso è esteso ad una variabile
aleatoria Y = f(X) definita, a partire dalla variabile aleatoria X, attraverso la funzione deterministica
f.
In questo paragrafo si considera una variabile aleatoria Z definita attraverso una funzione
deterministica f(X,Y) sulla base di due variabili aleatorie X e Y. Il valore atteso della variabile
aleatoria Z è definito come la media dei possibili valori = f(,) assunti da Z, pesati attraverso la
loro probabilità di occorrenza pXY(,)dd:
E Z E f X , Y
f , p , d d
XY
(1.133)
Dalla seconda delle (1.131) discende che se X e Y sono statisticamente indipendenti, allora
E f X g Y E f X E g Y
(1.134)
per ogni funzione f e g per qui i valori attesi esistono.
1.8.5 Somma di variabili aleatorie statisticamente indipendenti
Sia Z = X + Y, con X e Y statisticamente indipendenti. La funzione caratteristica di Z può essere
espressa nella forma:
Z E ei z E e
i X Y
E ei X E ei Y X Y
(1.135)
in cui è stata impiegata la (1.134). Dalla (1.135) discendono banalmente le seguenti relazioni:
pZ
p p d
X
Y
(1.136)
Z X Y
j Z j X j Y
j 1, 2,...
(1.137)
(1.138)
1.8.6 Correlazione e covarianza
Date due variabili aleatorie X e Y, si definisce correlazione il valore atteso del loro prodotto:
46
RXY E XY
p , d d
(1.139)
XY
Dalla definizione si evince che la correlazione di X rispetto a X stessa coincide con la media
quadratica (RXX = X2).
Si definisce covarianza il valore atteso del prodotto delle variabili X e Y centrate rispetto alla loro
media:
CXY E X X Y Y
p , d d
X
Y
XY
(1.140)
La covarianza della variabile aleatoria X rispetto a se stessa coincide con la varianza (CXX = X2).
Correlazione e covarianza sono legate dalla relazione:
RXY CXY X Y
(1.141)
Si definisce covarianza normalizzata (o coefficiente di correlazione) il rapporto:
XY
C XY
ˆ ˆ
E XY
X Y
(1.142)
dove X̂ e Yˆ sono le versioni standardizzate di X e Y.
Le variabili aleatorie X e Y sono dette non-correlate se le loro covarianza CXY è nulla. Se X e Y sono
statisticamente indipendenti, allora sono anche non-correlate. Questa affermazione può essere
facilmente verificata ricordando che se X e Y sono statisticamente indipendenti, allora la loro
densità di probabilità congiunta può essere fattorizzata nella forma: pXY(,) = pX()pY().
Sostituendo nella (1.140) si dimostra immediatamente che CXY=0.
L’implicazione opposta non è, in generale, vera: due variabili aleatorie non-correlate non sono, in
generale, statisticamente indipendenti.
La covarianza e la covarianza normalizzata sono limitate dalle relazioni:
C XY X Y
(1.143)
XY 1
Nelle quali l’uguaglianza si verifica nel caso X è Y sono legate da una relazione lineare del tipo
Y=aX + b. La (1.143) può essere dimostrata notando che la seguente disuguaglianza è valida per
ogni a in
2
E a X X Y Y 0
a
(1.144)
Espandendo l’espressione contenuta nel valore atteso e utilizzando le definizioni di varianza e
covarianza, si ottiene la disequazione di secondo grado:
2X a2 2CXY a Y2 0
a
(1.145)
47
La quale è soddisfatta a condizione che il discriminante sia minore o uguale a zero; dunque:
2
CXY
2X Y2 0
(1.146)
da cui discendono banalmente le (1.143).
Esempio 1.13. Realizzazioni di una coppia di variabili aleatorie
Si considerano le variabili aleatorie X e Y caratterizzate dai seguenti parametri: X = 10, Y
= 20, X2 = 10, Y2 = 5. La Figura 1-44 mostra 1000 realizzazioni di X e Y per diversi
valori di covarianza: CXY = 0 (a), CXY = 3 (b), CXY = 7 (c), CXY = -5 (d). A questi quattro casi
corrispondono i valori di covarianza normalizzata XY = 0, 0.42, 0.99, -0.71.
28
28
26
26
24
24
20
y
y
22
20
18
18
16
16
14
12
22
14
0
2
4
6
8
10
x
12
14
16
18
20
2
4
6
8
10
x
(a)
12
14
16
18
20
(b)
26
26
24
24
22
22
y
y
20
20
18
18
16
16
14
14
0
2
4
6
8
10
12
14
16
18
x
0
2
4
6
(c)
8
10
x
12
14
16
18
(d)
Figura 1-44. Realizzazioni di una coppia di variabili aleatorie.
Esempio 1.14. Coefficiente di correlazione e dipendenza lineare
Il coefficiente di correlazione può essere interpretato come una misura della dipendenza
lineare che intercorre fra due variabili aleatorie. In particolare, due variabili X e Y sono
legate da una legge deterministica lineare se e solo se il loro coefficiente di correlazione è
1. Infatti, se Y = aX con aℝ deterministico, allora risulta:
Y E Y E aX a X
2
2
Y2 E Y Y E a 2 X X a 2 2X
(1.147)
2
Cxy E X X Y Y E a X X a2X
Dalla seconda delle (1.147) si deduce che Y = |a|X, quindi sostituendo nella (1.142) si
ottiene:
XY
a
sgn a
a
(1.148)
48
La Figura 1-45 mostra 1000 realizzazioni di una coppia di variabili aleatorie perfettamente
non-correlate, ma legate da un’evidente relazione statistica (non-lineare).
6
4
y
2
0
-2
-4
-6
-4
-2
0
2
4
6
8
x
Figura 1-45. Coppia di variabili aleatorie con legame non-lineare.
1.8.7 Modello normale bi-variato
Due variabili aleatorie X e Y sono dette congiuntamente normali se la loro densità di probabilità
congiunta è fornita dalla relazione:
p XY ,
1
2 X Y 1 2XY
X 2 Y 2 2 XY X Y
1
exp
2
2 1 2XY 2X
Y
X
Y
(1.149)
Oppure se la loro funzione caratteristica congiunta ha la forma:
1
XY , exp i X Y exp 2X 2 2CXY Y2
2
(1.150)
1.8.8 Distribuzione condizionata di probabilità di una variabile aleatoria
Siano A e B due eventi legati ad un medesimo esperimento. La probabilità di occorrenza dell’evento
A condizionata all’occorrenza dell’evento B è definita dalla relazione (1.10):
P A | B
P A B
P B
P B 0
(1.151)
Si assuma ora che gli eventi A e B siano determinati da due variabili aleatorie X e Y come segue:
A X ;
B Y
,
(1.152)
Sfruttando la definizione di distribuzione di probabilità, la (1.151) può essere riscritta nella forma:
P X | Y FX | Y
FXY ,
FY
(1.153)
49
Dove la funzione FX(|Y) è detta distribuzione di probabilità condizionata della variabile X
rispetto all’evento {Y}. La corrispondente funzione di densità di probabilità è ottenuta derivando
la (1.153) rispetto a e risulta:
p X | Y
FXY ,
FY
1
(1.154)
Si consideri ora il caso in cui l’evento che genera la condizione sia B = {1 < Y 2}. La
distribuzione di probabilità di X condizionata all’occorrenza di B risulta:
FX | 1 Y 2
FXY , 2 FXY , 1
FY 2 FY 1
(1.155)
La corrispondente densità di probabilità può essere ottenuta derivando la (1.155) rispetto a e
risulta:
2
p X | 1 Y 2
p , d
XY
1
FY 2 FY 1
(1.156)
avendo sfruttato la relazione:
FXY ,
pXY , d
(1.157)
Sostituendo 1= e 2 = + , la (1.156) può essere riscritta nella forma:
p X | Y
pXY , d
FY FY
(1.158)
che, per 0 risulta:
p X |Y |
p XY ,
pY
(1.159)
dove, la notazione pX|Y(|) indica la densità di probabilità di X condizionata all’occorrenza di Y in
un intono infinitesimo di .
Dalla (1.159) deriva banalmente il teorema della probabilità totale (o di Bayes) che si esprime
attraverso la relazione:
pX |Y | pY pY | X | pX
(1.160)
Confrontando le equazioni (1.131) e (1.159) si deduce che se le variabili aleatorie X e Y sono
statisticamente indipendenti, allora valgono le relazioni:
50
p X |Y | pX
pY | X | pY
(1.161)
1.9 Proprietà delle variabili aleatorie Gaussiane
Il modello Gaussiano è largamente il più diffuso grazie a una serie di proprietà che lo distinguono.
Fra queste, si menzionano le tre più rilevanti: variabili Gaussiane non-correlate sono statisticamente
indipendenti; la somma di variabili aleatorie Gaussiane è Gaussiana; la somma di un gran numero di
variabili aleatorie statisticamente indipendenti comunque distribuite tende a essere Gaussiana.
1.9.1 Indipendenza statistica di variabili non-correlate
Siano X e Y due variabili Gaussiane non-correlate XY 0 . La densità di probabilità congiunta
fornita dalla (1.149) risulta:
1 2 2
1
X
Y
p XY ,
exp
2
2
2 X
2 X Y
Y
(1.162)
che può essere chiaramente fattorizzata in due termini corrispondenti con le espressioni della
densità di probabilità di due variabili Gaussiane. Ciò dimostra l’indipendenza statistica.
1.9.2 Linearità dello spazio delle variabili Gaussiane
Uno spazio vettoriale è detto lineare se contiene ogni combinazione lineare dei membri dello spazio
stesso. Per dimostrare che lo spazio delle variabili Gaussiane è lineare è sufficiente dimostrare che
se X e Y sono Gaussiane allora Z = aX + bY è Gaussiana per ogni a e b in ℝ. In realtà, è evidente
che la semplice scalatura di una variabile Gaussiana ha distribuzione Gaussiana (è possibile
verificarlo con un cambio di variabile nella (1.68)), allora senza perdita di generalità è possibile
porre a = b = 1 e quindi Z = X + Y.
Applicando la definizione di distribuzione di probabilità si osserva che la distribuzione di
probabilità di Z risulta:
FZ P Z P X Y
p d
Z
p XY , d d
(1.163)
p , d d
XY
in cui l’ultimo passaggio è eseguito operando la sostituzione - . Inoltre, confrontando la
seconda e la terza riga della (1.163) si deduce la relazione:
pZ
p , d
XY
(1.164)
La (1.164) dimostra che la densità di probabilità della somma di due variabili aleatorie
statisticamente indipendenti è fornita dalla convoluzione della loro densità marginale. Applicando la
trasformata di Fourier alla (1.164) si ottiene la funzione caratteristica di Z nella forma:
51
Z
XY
e p , d d
i
e
i
ei p XY , d d
(1.165)
XY ,
in cui si è moltiplicato e diviso per la medesima quantità ei e si è applicata la definizione di
funzione caratteristica congiunta. Sostituendo l’espressione di XY pertinente per il modello
Gaussiano (Eq. (1.150)) si ottiene la relazione:
1
Z exp i X Y exp 2X 2CXY Y2 2
2
(1.166)
che corrisponde alla funzione caratteristica di una variabile Gaussiana con media Z = X + Y e
varianza Z2 = X2 + 2CXY + Y2.
1.9.3 Teorema del limite centrale
Si consideri un insieme di variabili aleatorie Xj (j = 1,…, n) statisticamente indipendenti con media
X e varianza X2; Yn sia la variabile aleatoria definita attraverso la somma:
n
Yn X j
(1.167)
j 1
Applicando la definizione di media e varianza, e tenendo conto dell’indipendenza delle Xj, risulta:
Yn n X
(1.168)
Y2n n2X
La versione standardizzata di Yn è fornita dalla relazione:
Y n X
Yˆn n
n X
(1.169)
1 n ˆ
Xj
n j 1
dove Xˆ j ( X j X ) / X . La funzione caratteristica di Yˆn risulta:
Yˆ E exp i Yˆn
n
i n ˆ
E exp
X j
n
j
1
(1.170)
n
i ˆ
E exp
X j
n
j 1
Tenendo conto che le Xj sono statisticamente indipendenti, il valore atteso nella (1.170) può essere
fattorizzato nella forma:
52
n
i ˆ
Yˆ E exp
X j
n
n
j 1
(1.171)
Se n è grande, gli esponenziali nella (1.171) possono essere espansi in serie di Taylor
n
i
3
2 ˆ 2
Yˆ E 1
Xˆ j
X j O n 2
n
2n
n
j 1
2
i
ˆ E Xˆ 2
1
E
X
j
j
n 2n
j 1
(1.172)
n
che, tenendo conto che le Xˆ j sono standardizzate, risulta3:
2
Yˆ 1
n
2n
n
(1.173)
Il limite per n della (1.173) fornisce:
1
Yˆ exp 2
n
2
(1.174)
che è la funzione caratteristica di una variabile Gaussiana con media nulla e varianza unitaria.
1.9.4 Simmetria polare delle variabili Gaussiane
Se X e Y sono variabili Gaussiane standardizzate e statisticamente indipendenti, allora le curve di
livello della densità di probabilità congiunta sono circonferenze. L'osservazione può essere
dimostrata scrivendo pXY nella forma:
pXY ,
2 2 1
2
1
exp
exp
2
2 2 2
2
(1.175)
dove ρ2 = ξ2 + η2. Questa proprietà, peculiare della distribuzione Gaussiana, fa sì che il vettore
X X , Y sia statisticamente invariante rispetto alla rotazione del sistema di riferimento.
1.9.5 Variabili Gaussiane e cumulanti
Una variabile Gaussiana X ha tutti i cumulanti di ordine maggiore di 2 nulli. Ciò può essere
verificato notando che la log-funzione caratteristica di una v.a. Gaussiana ha la forma:
1
i X 2X 2
2
(1.176)
che corrisponde alla (1.51) avendo posto 1 X , 2 2X e j 0 per j 2 .
In conseguenza di questa proprietà i cumulanti di grado >2 possono essere usati come misura di
non-Gaussianità.
n
3
x
Si considera il limite notevole lim 1 e x
n
n
53
1.9.6 Variabili Gaussiane e massima entropia
In accordo con il principio di massima entropia, assegnati un insieme di vincoli E Fj X c j , la
variabile aleatoria meno strutturata possibile ha densità di probabilità nella forma:
n
p0 A exp a j Fj
j 0
(1.177)
Se si assume F1(X) = X e F2(X) = X2, allora le condizioni di vincolo su p0 sono espresse dalle
relazioni:
p0 d 1
p0 d E X X
(1.178)
2 p0 d E X 2 X2 2X
Sostituendo la (1.177) nella (1.178) si ottengono i valori delle costanti a1, a2 e A:
a1
X
X2
a2
A
1
2X2
(1.179)
2
1
exp X2
2X
2X
che sostituite nella (1.177) forniscono:
X 2
1
p0
exp
2X2
2 X
(1.180)
Si deduce che, assegnata media e varianza, la distribuzione Gaussiana fornisce la massima possibile
entropia. In altre parole, le variabili aleatorie Gaussiane sono quelle meno strutturate ("più
aleatorie") possibile.
Grazie a questo principio, l'entropia può essere impiegata come misura di non-Gaussianità. Allo
scopo di rimuovere la dipendenza dalla varianza, si introduce la neg-entropia:
J X H XG H X
(1.181)
dove XG è una v.a. Gaussiana avente varianza pari alla varianza di X.
H XG
1
log
2
2 X
(1.182)
La neg-entropia così definita è una quantità non-negativa e si annulla solo se X ha distribuzione
Gaussiana.
Equation Chapter (Next) Section 1
54
2
Vettori Aleatori
2.1 Definizione
Definiamo vettore aleatorio un vettore di variabili aleatorie o, con maggior precisione, una variabile
aleatoria le cui realizzazioni sono in uno spazio multi-dimensionale (es. ℝn).
n
x = X()
x
Figura 2-1. Vettore aleatorio X.
Un vettore aleatorio è rappresentato specificando le proprietà statistiche congiunte delle sue
componenti. Si definisce distribuzione di probabilità congiunta la funzione
FX P X1 1
X n n
(2.1)
definita per ℝn; Xj e j (j = 1,…,n) sono le componenti di X e , rispettivamente. La distribuzione
di probabilità di un vettore aleatorio ha proprietà analoghe alla distribuzione di probabilità di una
variabile aleatoria scalare; in particolare:
FX :
n
[0,1]
FX 0 se 1 ,
, n
FX 1 se 1 ,
, n
(2.2)
Se le componenti Xj di X sono variabili aleatorie continue, può essere definita la densità di
probabilità congiunta attraverso la relazione:
n FX
pX
1... n
(2.3)
La funzione caratteristica di X è fornita dalla trasformata di Fourier n-dimensionale della densità di
probabilità e risulta:
X E exp i T X
i
e pX d
T
(2.4)
n
2.2 Momenti statistici
Si definisce media del vettore X il vettore contenente la media delle sue componenti.
55
X1
X 2
X E X
X n
(2.5)
Si definisce matrice di correlazione del vettore X:
2X1
RX X
T
R X E XX 2 1
RX X
n 1
RX 1 X n
2X n
RX 1 X 2
2X 2
(2.6)
Gli elementi diagonali della matrice di correlazione sono le medie quadratiche delle componenti di
X; gli elementi fuori diagonale rappresentano le correlazioni di tutte le possibili coppie di
componenti.
Si definisce matrice di covarianza del vettore X:
2X1
T
C X X
CX E X X X X 2 1
C X X
n 1
C X1 X 2
2X 2
C X1 X n
2X n
(2.7)
Gli elementi diagonali della matrice di covarianza sono le varianze delle componenti di X; gli
elementi fuori diagonale rappresentano le covarianze di tutte le possibili coppie di componenti.
Le matrici di correlazione e di covarianza sono legate dalla relazione:
CX R X X TX
(2.8)
La matrice di correlazione rappresenta la generalizzazione del concetto di media quadratica al caso
di vettore aleatorio, mentre la matrice di covarianza generalizza il concetto di varianza. Queste
matrici possono essere quindi interpretate, rispettivamente, come il momento statistico di ordine 2 e
il momento statistico centrale di ordine 2 del vettore X. Da un punto di vista concettuale, non vi
sono preclusioni a considerare momenti statistici di ordine superiore al secondo. In questo caso
nascono però difficoltà formali in quanto tali grandezze non possono essere espresse sinteticamente
attraverso il prodotto “riga per colonna” come nelle (2.7) e (2.8).
2.3 Modello normale (Gaussiano)
Un vettore aleatorio X ha distribuzione normale (o Gaussiana) se la sua densità di probabilità è nella
forma:
pX
1
2
n2
CX
12
T
1
exp X CX1 X
2
(2.9)
Si osserva che la densità di un vettore Gaussiano è definita dalla media e dalla matrice di
covarianza. Inoltre, si osserva che la densità di probabilità congiunta della coppia di variabili
56
aleatorie X e Y espressa dalla (1.149) può essere rappresentata in forma compatta attraverso la (2.9)
ponendo X = [X Y]T.
La funzione caratteristica di X risulta:
1
X exp i T X exp TCX
2
(2.10)
Se X è un vettore di variabili aleatorie Gaussiane non correlate a media nulla, la densità di
probabilità assume la forma:
pX ξ
1
1
exp ξ Tξ
n /2
2
2
(2.11)
1
1 2
exp ξ
n /2
2
2
La densità di probabilità dipende soltanto dalla norma di ξ, quindi ha simmetria polare, cioè le
superfici di livello sono iper-sfere. La medesima proprietà vale per la funzione caratteristica.
2.4 Grandezze statistiche di ordine superiore al secondo
Passando dalle v.a. aleatorie scalari a quelle vettoriali, i momenti statistici di ordine 1 e 2 sono
generalizzati utilizzando quantità vettoriali (ordine 1, media) e matriciali (ordine 2, matrice di
correlazione). Analogamente il ruolo del secondo cumulante è assunto dalla matrice di covarianza.
La trattazione di grandezze statistiche di ordine superiore è formalmente più complessa e dà luogo a
quantità di natura sensoriale. Ciò e reso evidente espandendo in serie di McLaurin la funzione
caratteristica per generare i momenti statistici:
X
j 1 d j
n
X θ 1
j
θ0
1
2
2 X
j , k 1 j k
n
j k
θ0
r X
1 n
r ! j1 , , jr 1 j1 jr
j1
jr
(2.12)
θ 0
in cui le derivate parziali di ordine r in θ = 0 rappresentano il valore atteso del prodotto di tutte le
possibili sequenze di r componenti Xj di X.
E X j1 ... X jr
1 r X
i r j1 ... jr
(2.13)
θ 0
La proliferazione dei momenti statistici può essere formalmente controllata adottando il formalismo
dell'algebra di Kronecker (Appendice C). In questo modo, il momento statistico di ordine j del
vettore X si esprime nella forma:
m j X E X j
(2.14)
dove j rappresenta la potenza di Kronecker j-esima. Se X ha dimensione n, allora m j X ha
dimensione nj e contiene il valore atteso dei prodotti di tutte le possibili sequenze di j componenti di
T
X. Se ad esempio X X1 , X 2 , allora:
57
m 2 X 12 X 1 X 2 X 2 X 1 X 22
m3 X 13
X 12 X 2
T
X 1 X 22
X1 X 2 X1
X 2 X 12 X 2 X 1 X 2
X 22 X 1 X 23
T
(2.15)
Si osserva che il vettore m2 contiene i medesimi termini di RX.
Sfruttando questa notazione, la funzione caratteristica di X assume la forma:
i j T j
θ mj X
j 1 j !
X θ 1
(2.16)
Analogamente la log-funzione caratteristica assume la forma:
i j T j
X θ θ κ j X
j 1 j !
(2.17)
dove κ j X sono i cumulanti di X.
2.5 Entropia ed informazione mutua
L'entropia di un vettore aleatorio è definita esattamente come nel caso scalare
H X
p ξ log p ξ dξ
X
X
(2.18)
n
con la differenza che l'integrazione avviene su uno spazio di dimensione n.
Si definisce informazione mutua fra le componenti di X la grandezza:
n
I X 1 , X 2 ,... X n H X j H X
(2.19)
j 1
Interpretando l'entropia come misura del contenuto di informazione, I rappresenta una misura di
quanto l'informazione contenuta nelle diverse componenti di X si sovrappone. L'informazione
mutua è un numero non-negativo ed è zero se e solo se le componenti di X sono statisticamente
indipendenti.
2.6 Rappresentazione di vettori aleatori
Passando dal caso di una variabile aleatoria X a valori scalari (le cui realizzazioni x sono in ℝ) al
caso di un vettore aleatorio X (le cui realizzazioni x sono in ℝn) si pone il problema di scegliere la
base in ℝn più opportuna da adottare. La scelta non è univoca ed esistono diversi criteri che si
adattano più o meno bene alle diverse circostanze. Fra tutti i sistemi di riferimento è opportuno
menzionare il riferimento utilizzato nell’analisi a componenti principali (Principal Component
Analysis, PCA).
2.6.1 Analisi a componenti principali (PCA)
Si consideri un vettore aleatorio X con realizzazioni in ℝn che per semplicità assumiamo a media
nulla. Ci poniamo l’obiettivo di individuare un vettore ℝn che rappresenti la direzione tipica di
X, quindi che sia più parallelo possibile alle realizzazioni di X. Ciò può essere ottenuto
massimizzando una misura di parallelismo, ad esempio:
58
2
J E T X
(2.20)
con il vincolo ||||=1 (altrimenti sarebbe sufficiente allungare per incrementare J). La
massimizzazione vincolata della (2.20) può essere sostituita dalla massimizzazione della funzione
ausiliaria:
2
J E T X
2
(2.21)
dove è un moltiplicatore di Lagrange. I punti di stazionarietà (fra cui il massimo) di J possono
essere ottenuti annullando le derivate di J rispetto alle componenti di ottenendo l’equazione:
E XXT 0
(2.22)
che corrisponde al problema agli autovalori:
CX I 0
(2.23)
La matrice di covarianza è simmetrica e definita positiva, quindi gli autovettori k (k=1,…,n) sono n
e sono mutuamente ortonormali; i corrispondenti autovalori k sono reali e positivi. Gli autovalori
sono convenzionalmente ordinati in modo decrescente.
Gli autovettori k formano una base ortonormale in ℝn, quindi possono essere impiegati per
rappresentare il vettore aleatorio X (o più esattamente le sue realizzazioni x).
n
X k Yk
(2.24)
k 1
dove le variabili aleatorie Yk (k=1,…,n) sono le proiezioni di X sui vettori k
Yk kT X
(2.25)
e sono dette componenti principali del vettore aleatorio X. Si dimostra che le componenti principali
hanno media nulla, sono mutuamente non-correlate e hanno varianza pari agli autovalori
E Yk kT E X kT X 0
E YhYk hT E XXT k hTCXk k hk
(2.26)
La (2.24) rappresenta il vettore X come una somma di vettori deterministici k modulati da variabili
aleatorie non-correlate con media nulla e varianza k. Se gli autovalori sono ordinati in modo
decrescente, la (2.24) fornisce una rappresentazione gerarchica di X, in cui i primi termini della
somma tendono a essere dominanti rispetto a quelli successivi. Quando la (2.24) è utilizzata per
analizzare statisticamente un insieme di dati misurati, queste proprietà gerarchiche possono essere
utilizzate per separare la parte significativa dei dati dal rumore sperimentale.
L’analogia fra la (2.24) e la rappresentazione modale della risposta di strutture lineari è evidente. In
entrambi i casi le coordinate naturali del problema sono sostituite da un sistema di coordinate
opportuno in modo da consentire un troncamento modale (considerare un numero di termini m<n
nella somma dell’Eq. (2.24)). In entrambi i casi, il cambio di coordinate comporta vantaggi
59
aggiuntivi: nel caso dell’analisi modale, le coordinate principali sono determinate da equazioni del
moto disaccoppiate (per sistemi con smorzamento proporzionale), mentre nel caso di vettori
aleatori, le componenti principali sono statisticamente non-correlate.
La (2.24) può essere riscritta in forma compatta
X Y
(2.27)
dove la matrice , ottenuta assemblando per colonne gli autovettori, è una matrice ortogonale e
rappresenta una rotazione in ℝn.
2.7 Simulazione di vettori Gaussiani
Realizzazioni x di un vettore Gaussiano X con media X e matrice di covarianza CX possono essere
generate sfruttando la relazione (2.27) e le proprietà delle componenti principali.
Sia z una realizzazione del vettore aleatorio Z, le cui componenti hanno distribuzione Gaussiana,
media nulla, varianza unitaria e sono mutuamente non-correlate (e quindi statisticamente
indipendenti per la Gaussianità). Realizzazioni di questo vettore possono essere ottenute attraverso
le funzioni disponibili in ogni ambiente computazionale per la generazione di numeri casuali
Gaussiani statisticamente indipendenti. Dato z, una realizzazione di x può essere ottenuta attraverso
la relazione:
x X 0.5z
(2.28)
dove = diag(1…n) è la matrice degli autovalori di CX.
Esempio 2.1. Simulazione di vettori aleatori Gaussiani
Il codice riportato in Figura 2-2 simula una serie di realizzazioni di un vettore aleatorio
Gaussiano con assegnata media e matrice di covarianza.
function x = randn_multi(N, mu, C)
% genera N realizzazioni di un vettore aleatorio Gaussiano con media mu e
% matrice di covarianza C
% x ha dimensione length(mu), N
n = length(mu);
[F,L] = eig(C);
y = sqrt(L)*randn(n,N);
x = F*y;
for k=1:n
x(k,:) = x(k,:) + mu(k);
end
Figura 2-2. Codice Matlab per simulazione di vettori aleatori Gaussiani.
Equation Chapter (Next) Section 1
60
3
Processi aleatori
Un processo stocastico (o aleatorio) è una legge che associa, ad ogni punto dello spazio
campionario Ω una funzione x(t) dipendente da un parametro t (nelle applicazioni trattate nel
seguito rappresenterà sempre il tempo). In questo senso, un processo aleatorio può essere
interpretato come la generalizzazione del concetto di variabile aleatoria, ammettendo che questa
assuma valori nello spazio delle funzioni, anziché in .
3.1 Definizioni
Si consideri un esperimento il cui risultato è una funzione del tempo (l’accelerazione sismica del
suolo, la velocità del vento, la risposta di un sistema dinamico). Ogni storia temporale x(t) derivante
da un esperimento è interpretata come una possibile realizzazione di un processo aleatorio X(t). Le
realizzazioni sono dette funzioni campione (Figura 3-1).
Figura 3-1. Funzioni campione.
Un processo aleatorio X(t) può essere interpretato come un contenitore per le funzioni x(j)(t)
(j=1,2,…) ottenute in corrispondenza del risultato j di un qualche esperimento (o osservazione). In
questo senso, fissando il parametro t = t1, il processo aleatorio si reduce ad una variabile aleatoria
X1=X(t1), mentre fissando l’indice j, il processo aleatorio si riduce ad una funzione deterministica
(Figura 3-2).
Figura 3-2. Variabile aleatoria estratta da un processo aleatorio.
61
Si considerino un insieme di variabili aleatorie X1,...,Xn estratte dal processo X(t) in corrispondenza
degli istanti t = t1,...,tn (Figura 3-3). La loro completa descrizione probabilistica è fornita dalla
densità di probabilità congiunta:
pX1 X 2
Xn
1 , 2 ,
, n pX t1 X t2
X tn
1, 2 ,
, n
(3.1)
È chiaro che la (3.1) descrive il processo aleatorio X(t) tanto più accuratamente quanto più grande è
l’ordine della distribuzione congiunta considerata. Si deve osservare, tuttavia che anche se si
arrivasse idealmente a considerare una distribuzione congiunta di ordine infinito, estraendo un
numero infinito di variabili aleatorie dal processo X(t), si tratterebbe comunque di una
rappresentazione parziale4 del processo aleatorio, perché esso è formato da un’infinità nonnumerabile di variabili aleatorie. Questo tipo di rappresentazione è comunque sufficiente per gli
scopi della presente trattazione.
Figura 3-3. Insieme di variabili aleatorie estratte da un processo aleatorio.
3.1.1 Medie statistiche del primo ordine
Si consideri la variabile aleatoria X1 estratta dal processo X(t) per t = t1. Essa è completamente
descritta dalla densità di probabilità pX(t1)(). Le medie statistiche del primo ordine includono i
momenti statistici della variabile aleatoria X1 = X(t1). In particolare, la media, la media quadratica e
la varianza del processo aleatorio X(t) sono definite attraverso le relazioni:
X t1 E X t1
1 pX t1 1 d1
(3.2)
2
2X t1 E X t1 12 pX t1 1 d1
(3.3)
2
2
2X t1 E X t1 X t1 1 X t1 p X t1 1 d1
(3.4)
e sono dunque funzioni (deterministiche) del tempo. La varianza e la media quadratica sono legate
dalla relazione:
2X t1 2X (t1 ) 2X t1
(3.5)
4
Una rappresentazione completa di un processo aleatorio può essere ottenuta attraverso il funzionale caratteristico
(generalizzazione della funzione caratteristica definita per le variabili aleatorie).
62
3.1.2 Medie statistiche del secondo ordine
Si considerino due variabili aleatorie X1 e X2 estratte dal processo X(t) nei due istanti t = t1 e t = t2.
Le medie statistiche del secondo ordine coinvolgono la rappresentazione congiunta delle variabili
X1 e X2, estratte dal processo per ogni possibile coppia di istanti t1 e t2. Ciò avviene, in generale,
attraverso la funzione di densità di probabilità congiunta pX(t1)X(t2)(1, 2), oppure attraverso momenti
statistici congiunti quali correlazione e covarianza. Si definiscono auto-correlazione e autocovarianza le due seguenti grandezze:
RXX t1 , t2 E X t1 X t2
1 2
p X t1 X t2 1 , 2 d1 d2
(3.6)
C XX t1 , t2 E X t1 X t1 X t2 X t2
1 X t1 2 X t2 pX t1 X t2 1 , 2 d1 d2
(3.7)
da cui si evince che l’auto-correlazione e l’auto-covarianza sono funzioni deterministiche in 2 e
sono legate dalla relazione:
CXX
t1 , t2 RXX t1 , t2 X t1 X t2
(3.8)
L’auto-covarianza normalizzata è definita dal rapporto:
XX t1 , t2
C XX t1 , t2
X t1 X t2
(3.9)
Dalle (3.6), (3.7) e (3.9) discendono immediatamente le seguenti proprietà:
RXX t1 , t2 RXX t2 , t1
C XX t1 , t2 C XX t2 , t1
XX t1 , t2 XX t2 , t1
(3.10)
RXX t1 , t1 2X (t1 )
C XX t1 , t1 2X t1
XX t1 , t1 1
3.2 Processi aleatori stazionari
Un processo aleatorio è definito stazionario se la sua densità di probabilità congiunta di ordine n è
indipendente da una traslazione dell’origine dell’asse del tempo.
p X t1 1 p X t1 1
p X t1 X t2 1 , 2 p X t1 X t2 1 , 2
(3.11)
p X t1
X tn
1 ,
, n p X t1
X tn
1 ,
, n
Ponendo = -t1, si verifica immediatamente che la (3.11) implica le seguenti proprietà:
63
1. La densità di probabilità del primo ordine (pdf) è indipendente dal tempo t1;
2. La densità di probabilità congiunta di ordine 2 dipende soltanto dalla distanza t2 – t1 dei due
istanti considerati;
3. La densità di probabilità congiunta di ordine n dipende dalle n – 1 distanze t2 – t1, t3 – t2, …,
tn – tn-1 fra gli n istanti considerati per l’estrazione delle variabili aleatorie.
Un processo aleatorio X(t) è detto debolmente stazionario se le condizioni (3.11) sono verificate per
n ≤ 2.
Dalle (3.11) è immediato dimostrare che le medie statistiche del primo ordine di un processo
(debolmente) stazionario sono indipendenti dal tempo:
X E X t
p d
X t
2
2X E X t
2
p X t d
(3.12)
2
2
2X E X t X X p X t d
Analogamente, le medie statistiche del secondo ordine di un processo (debolmente) stazionario
dipendono dalla distanza = t2 – t1 fra i due istanti considerati per estrarre le variabili aleatorie. Tale
distanza è detta tempo di ritardo (o time lag):
RXX E X t X t
1 2
p X t X t 1 , 2 d 1 d 2
C XX E X t X X t X
1 X 2 X pX t X t 1 , 2 d 1 d 2
(3.13)
XX
C XX
2X
È immediato verificare che le funzioni definite dalle (3.13) soddisfano le seguenti proprietà:
RXX RXX
C XX C XX
XX XX
RXX 0 2X
(3.14)
C XX 0 2X
XX 0 1
Inoltre, per la (1.143) risulta:
64
C XX 2X
XX 1
(3.15)
Un’ulteriore proprietà dell’auto-covarianza può essere dedotta da considerazioni di natura fisica.
Quando le due variabili aleatorie X(t1) e X(t2) utilizzate per valutare la covarianza sono estratte in
istanti molto distanti tra loro (||), queste variabili aleatorie tendono ad essere statisticamente
indipendenti e quindi non-correlate. Da ciò risulta la proprietà:
lim CXX 0
(3.16)
Mentre le proprietà (3.14) e (3.15) hanno origine matematica e sono sempre rigorosamente
soddisfatte, la (3.16) ha un’origine di natura fisica e, in alcuni casi, può cadere in difetto. I processi
aleatori per i quali la (3.16) è valida sono detti a memoria finita.
La Figura 3-4 mostra una tipica funzione di auto-covarianza di un processo stazionario.
Figura 3-4. Funzioni di auto-covarianza di un processo stazionario.
Si osservi che, a rigore, le funzioni campione di un processo stazionario devono necessariamente
avere supporto infinito (devono essere definite su tutto ℝ). In realtà l’ipotesi di stazionarietà è
applicata ogniqualvolta che gli effetti di inizio e fine generati dalla non-stazionarietà sono
trascurabili perché hanno una durata molto limitata rispetto alla lunghezza della parte di processo in
cui le caratteristiche statistiche sono effettivamente invarianti rispetto a traslazioni del riferimento
temporale. Considerando il caso in cui il processo X(t) costituisce la forza applicata ad una struttura,
o la risposta dinamica della struttura stessa (spostamento, tensione, ecc.), allora l’ipotesi di
stazionarietà appare accettabile quando la scala dei tempi caratteristici della struttura è molto più
rapida della scala temporale su cui variano le caratteristiche statistiche del processo. Un tempo
caratteristico di una struttura può essere, ad esempio, il primo periodo proprio ed è generalmente
dell’ordine di un secondo. Il tempo caratteristico delle forze applicate alla struttura dipende dalla
natura fisica del fenomeno eccitatore. Nel caso del vento, le proprietà statistiche della turbolenza
tendono a conservarsi invariate su periodi di lunghezza compresi fra 10 minuti e un’ora. Nel caso
delle onde marine il periodo di stazionarietà tende ad essere anche maggiore (circa 3 ore). Nel caso
del sisma, la fase pseudo-stazionaria in cui le caratteristiche dell’accelerazione sono invarianti dura
pochi secondi. Con questi argomenti è chiaro come l’ipotesi di stazionarietà sia assai più
ragionevole nel caso di strutture eccitate dal vento e dalle onde marine rispetto al caso di forzante
sismica.
65
3.2.1 Medie temporali di una funzione campione
La stima delle quantità statistiche definite dalle (3.12) e (3.13) può essere effettuata sulla base della
conoscenza di un insieme di realizzazioni xj(t) (j = 1,…,n) del processo X(t), utilizzando la
definizione frequentista di probabilità:
X
1 n
x j t
n j 1
2X
1 n 2
x j t
n j 1
2
1 n
x jt X
n j 1
2
X
RXX
1 n
x jt x jt
n j 1
C XX
1 n
x jt X x jt X
n j 1
(3.17)
È chiaro che, se il processo è effettivamente stazionario, le quantità statistiche stimate attraverso le
(3.17) dovranno essere invarianti rispetto a t e potranno quindi essere valutate per un t qualsiasi.
Questo comporta ovviamente un uso poco efficiente delle informazioni statistiche contenute nelle
realizzazioni xj(t) disponibili per l’analisi e può portare a stime poco accurate (se n non è grande a
sufficienza). Con l’obiettivo di migliorare l’efficienza della stima, si definiscono le medie temporali
di una funzione campione x(t) attraverso le relazioni che seguono. Si definisce media temporale
della funzione campione x(t) il valore deterministico:
x lim
T
1 T /2
x t d t
T T /2
(3.18)
Si definisce media quadratica temporale della funzione campione x(t) il valore deterministico:
x 2 lim
T
1 T /2 2
x t d t
T T /2
(3.19)
Si definisce varianza temporale della funzione campione x(t) il valore deterministico:
T /2
2
1
s lim
x t x d t x 2 x 2
T T
T /2
2
(3.20)
Si definisce auto-correlazione temporale della funzione campione x(t) la funzione deterministica:
rxx lim
T
1 T /2
x t x t dt
T T /2
(3.21)
Si definisce auto-covarianza temporale della funzione campione x(t) la funzione deterministica:
cxx lim
T
1 T /2
x t x x t x dt rxx x
T T /2
2
(3.22)
66
È possibile dimostrare che le funzioni rXX() e cXX() hanno le medesime proprietà di RXX() e di
CXX().
Le medie temporali del primo ordine di una funzione campione possono essere interpretate come
realizzazioni di variabili aleatorie che, in generale, assumono un valore diverso per ogni
realizzazione del processo aleatorio. In altri termini, le medie temporali di una funzione campione
sono realizzazioni di variabili aleatorie generate nel medesimo punto campionario che ha
generato la funzione campione.
Analogamente le medie temporali del secondo ordine di una funzione campione di un processo
stazionario possono essere interpretate come realizzazioni di processi aleatori (funzioni aleatorie del
tempo di ritardo ).
È semplice verificare che se X(t) è un processo stazionario i valori attesi delle sue medie temporali
coincidono con le corrispondenti medie statistiche (per la dimostrazione è sufficiente applicare
l’operatore di valore atteso alle (3.18) - (3.22)). Risulta dunque:
X E X
2X E X 2
2X E S 2
(3.23)
RXX E R XX
C XX E C XX
dove le lettere maiuscole sopralineate rappresentano le variabili aleatorie le cui realizzazioni sono
definite dai simboli minuscoli corrispondenti, mentre RXX() e CXX() sono i processi aleatori aventi
rXX e cXX come (generiche) funzioni campione.
3.2.2 Processi aleatori ergodici
Un processo aleatorio stazionario è detto ergodico se le medie temporali di ogni sua realizzazione
sono coincidenti, ovvero se le medie temporali delle sue realizzazioni sono deterministiche. In
questo caso le medie statistiche coincidono con le medie temporali calcolate a partire da una
qualsiasi funzione campione purché sufficientemente lunga (a rigore di lunghezza infinita):
X x
2X x 2
2X s 2
(3.24)
RXX rXX
C XX c XX
3.2.3 Rappresentazione nel dominio della frequenza di processi stazionari
L’analisi dei sistemi dinamici (deterministici) lineari è svolta in modo conveniente operando nel
dominio della frequenza. In questo modo, la trasformata di Fourier della risposta dinamica a regime
è ottenuta moltiplicando la trasformata di Fourier dell’eccitazione per la funzione di risposta in
frequenza del sistema dinamico. Allo scopo di estendere questi concetti all’analisi di sistemi lineari
con eccitazione aleatoria, è necessario introdurre una rappresentazione nel dominio della frequenza
di processi aleatori.
67
Nel caso di processi stazionari l’introduzione del concetto di trasformata di Fourier è piuttosto
complicato. Ciò è dovuto al fatto che la trasformata di Fourier di una funzione deterministica esiste
se e solo se questa è assolutamente integrabile (l’integrale del suo valore assoluto è finito). Per
contro, le funzioni campione di un processo stazionario non sono assolutamente integrabili, perché
non si estinguono per |t|. Da un punto di vista matematico, questo problema può essere risolto in
molti modi. Di seguito viene descritto quello matematicamente più semplice, che fa uso del
concetto di limite.
Sia x(t) una realizzazione del processo stazionario X(t) (per semplicità supposto a media nulla) e sia
xT(t) la funzione ottenuta finestrando x(t) in t(-T/2 T/2).
x t
xT t
0
T T
per t ,
2 2
altrimenti
(3.25)
Si supponga che xT(t) sia assolutamente integrabile per ogni T finito. La trasformata di Fourier di xT
è fornita dalla relazione:
xT
xT t e i t d t
T /2
T /2
x t e i t d t
(3.26)
ed esiste per ogni T finito, Mentre la xT(t) può essere espressa nella forma:
1
i t
xT t
e xT d
2
(3.27)
Si definisce energia della funzione xT(t) la grandezza scalare:
Enrg xT t
xT2 t dt
T /2
T /2
x 2 t dt
(3.28)
Essendo xT(t) una realizzazione di un processo aleatorio XT(t), l’energia può essere interpretata
come una variabile aleatoria. Il nome energia associato alla grandezza definita dalla (3.28) è dovuto
al fatto che essa corrisponde (a meno di una costante) all’energia cinetica nel caso in cui x(t)
rappresenta una velocità o all’energia potenziale, nel caso in cui x(t) rappresenti lo spostamento di
un sistema elastico. Il limite per T dell’energia diverge quando x(t) è una realizzazione di un
processo stazionario. Si definisce potenza della funzione xT(t) la grandezza scalare:
Pwr xT t
1 2
1 T /2 2
x
t
dt
x t dt
T T
T T /2
(3.29)
Confrontando la (3.29) con la (3.19) si osserva che il limite per T della potenza coincide con la
media quadratica temporale di x(t):
1
x lim Pwr xT t lim xT2 t d t
T
T T
2
(3.30)
La varianza del processo X(t) corrisponde al valore atteso della media quadratica temporale (X è a
media nulla per ipotesi), quindi risulta:
68
1
2
E X E lim X T2 t d t
T T
2
X
(3.31)
dove, l’integrale del processo XT(t) può essere interpretato come una variabile aleatoria le cui
realizzazioni sono ottenute integrando le funzioni campione xT(t) di XT(t). L’integrale nella (3.30)
può essere riscritto applicando il teorema di Parseval nella forma:
2
1
x t d t 2 xT d
2
T
(3.32)
La (3.32) è valida per ogni realizzazione xT(t), quindi può essere applicata per riscrivere la (3.31)
nella forma:
2
X
S d
(3.33)
XX
dove
S XX
2
1
1
lim E X T
T
2
T
(3.34)
In qui X T () è il processo aleatorio (funzione della frequenza) le cui realizzazioni sono le
trasformate di Fourier xT () ; la funzione SXX() è detta densità di potenza spettrale (Power
Spectral Density, PSD). Dalla (3.34) si deduce che la densità di potenza spettrale è una funzione
reale non-negativa.
L’auto-covarianza del processo X(t) può essere scritta come valore atteso dell’auto-covarianza
temporale:
T 2
1
C XX E lim X t X t d t
T T T 2
(3.35)
1
E lim X T t X T t d t
T T
dove, ancora, gli integrali sono interpretati come agenti su ogni realizzazione del processo X(t).
Sostituendo la (3.27) nella (3.35) si ottiene:
C XX
1
E Tlim
4 2T
i t
i t
e
X
d
e
X
d
dt
T
T
1
E lim 2
T 4 T
i t
i t *
e
X
d
X T d d t
e
T
1
E lim 2
T 4 T
i
*
e X T X T e
i t
(3.36)
d t d d
L’integrale in dt all’interno della (3.36) risulta:
69
e
i t
d t 2
(3.37)
che sostituito nella (3.36) fornisce la relazione:
1
C XX E lim
T 2T
e
i
e
i
2
X T d
(3.38)
S XX d
da cui si dimostra che la densità di potenza spettrale è, a meno di un fattore 2, la trasformata di
Fourier della funzione di auto-covarianza.
La densità di Potenza spettrale può essere espressa invertendo la (3.38) e risulta:
1
S XX
ei C XX d
2
(3.39)
Le equazioni (3.38) e (3.39) sono chiamate equazioni di Wiener-Khintchine.
Applicando la formula di Eulero alla (3.39) è possibile espandere l’esponenziale nella forma:
S XX
1
i
cos CXX d
sin CXX d
2
2
(3.40)
Ricordando che la funzione di auto-covarianza è pari rispetto a , il secondo integrale nella (3.40) si
annulla, pertanto la densità di potenza spettrale rimane espressa attraverso la relazione:
1
S XX
cos CXX d
2
(3.41)
S XX S XX
(3.42)
che è pari rispetto a
La (3.33) indica che l’area sottesa dalla densità di Potenza spettrale rappresenta la varianza del
processo. Inoltre, l’area elementare 2SXX()d rappresenta il contributo alla varianza X2 delle
armoniche del processo di pulsazione comprese nell’intervallo (, +d) (Figura 3-5). Per questa
ragione la densità di Potenza spettrale descrive il contenuto armonico del processo aleatorio così
come lo spettro di Fourier descrive il contributo armonico di un segnale deterministico.
70
Figura 3-5. Densità di Potenza spettrale.
3.3 Rappresentazione congiunta di una coppia di processi aleatori
Si consideri un esperimento il cui risultato è costituito da una coppia di processi aleatori X(t) e Y(t)
(per esempio il moto sismico lungo due direzioni o in due punti del terreno, la velocità del vento
misurata da due anemometri, la risposta dinamica di una struttura con 2 gradi di libertà).
Si consideri il valore del processo X(t) all’istante t = t1 e il valore del processo Y(t) per t = t2. Essi
possono essere interpretati come una coppia di variabili aleatorie e, come tali, possono essere
rappresentati attraverso la densità di probabilità congiunta pX(t1)Y(t2)(, ); quest'ultima dipende da
due parametri, e , nonché dai tempi t1 e t2 in cui le variabili aleatorie sono state estratte.
Dalla densità di probabilità congiunta si ottengono immediatamente le densità marginali dei
processi X e Y per integrazione parziale:
p X t1
p
pY t2
X t1 Y t2
, d
(3.43)
p
X t1 Y t2
, d
3.3.1 Medie statistiche congiunte del secondo ordine
Si definisce cross-correlazione dei processi X(t) e Y(t) la correlazione delle variabili aleatorie X(t1) e
Y(t2) estratte da X e Y agli istanti t1 e t2, rispettivamente:
RXY t1 , t2 E X t1 Y t2
p
X t1 Y t2
, d d
(3.44)
Analogamente, si definisce cross-covarianza di X e Y la funzione:
C XY t1 , t2 E X t1 X t1 Y t2 Y t2
t t p
X
1
Y
2
, d d
X t Y t
1
(3.45)
2
La cross-covarianza normalizzata è definita dalla relazione:
XY t1 , t2
C XY t1 , t2
X t1 Y t2
(3.46)
71
Il prefisso cross indica che la variabili aleatorie X(t1) e Y(t2) sono estratte dai due processi differenti
X e Y (sebbene associati al medesimo esperimento).
Dalle definizioni (3.44) - (3.46) risultano le proprietà:
RXY t1 , t2 RYX t2 , t1
C XY t1 , t2 CYX t2 , t1
(3.47)
XY t1 , t2 YX t2 , t1
In analogia a quanto definito per le variabili aleatorie, due processi aleatori X(t) e Y(t) sono detti
non-correlati se la loro cross-covarianza CXY(t1,t2) è nulla per ogni t1 e t2 in .
Appare evidente che le medie statistiche del secondo ordine di due processi stazionari X e Y non
dipendono da t1 e t2 separatamente, ma soltanto dal tempo di ritardo = t2 – t1.
RXY E X t Y t
p
X t Y t
, d d
C XY E X t X Y t Y
X Y pX t Y t , d d
(3.48)
XY
C XY
X Y
Dalle equazioni (3.48) è immediato verificare le seguenti proprietà:
RXY RYX
C XY CYX
(3.49)
XY YX
Inoltre per la (1.143) risulta:
C XY X Y
XY 1
(3.50)
Per le medesime ragioni fisiche esposte per l’auto-covarianza, anche la cross-covarianza
(generalmente) tende a zero per ||. La Figura 3-6 mostra una tipica funzione di crosscovarianza di due processi stazionari.
72
Figura 3-6. Cross-covarianza.
3.3.2 Densità di Potenza spettrale incrociata
Siano X(t) e Y(t) una coppia di processi stazionari a media nulla; si definisce densità di potenza
spettrale incrociata la funzione:
S XY
1
1
lim E X T YT*
2 T T
(3.51)
dove X T e YT sono i processi aleatori che contengono le Trasformate di Fourier delle realizzazioni
di X e Y finestrate secondo la (3.25). Operando in maniera analoga a quanto fatto per la densità di
potenza spettrale, è possibile dimostrare le relazioni:
C XY
e
i
S XY d
(3.52)
1
i
S XY
e CXY d
2
(3.53)
La densità di Potenza spettrale incrociata e la cross-covarianza costituiscono una coppia di Fourier.
La cross-covarianza è, in generale, non simmetrica, quindi la densità di Potenza spettrale incrociata
è, in generale, una funzione a valori complessi. La particolare simmetria della cross-covarianza
espressa dalla (3.49) si riflette sulle proprietà:
*
SYX S XY
S XY
(3.54)
3.3.3 Funzione di coerenza
La funzione di coerenza di due processi stazionari è definite dalla relazione:
XY
S XY
S XX SYY
(3.55)
La coerenza è, in generale, una funzione a valori complessi. Frequentemente, la sua parte reale è
chiamata co-coerenza, mentre la sua parte immaginaria è definita quad-coerenza. Alcuni testi
chiamano coerenza il modulo della (3.55), altri il suo modulo quadrato.
Una volta introdotta la funzione di coerenza, la densità di Potenza spettrale incrociata può essere
espresso nella forma:
73
S XY () S XX ()SYY () XY ()
(3.56)
La funzione di coerenza può essere interpretata come la controparte nel dominio della frequenza
della cross-covarianza normalizzata. Questa analogia si riflette nella proprietà:
XY () 1
(3.57)
Due processi aleatori che hanno coerenza unitaria sono detti coerenti. Se due processi aleatori
hanno coerenza nulla, allora sono non-correlati.
3.4 Trasformazioni lineari di processi stazionari
Si considerino due processi stazionari X(t) e Y(t) definiti in modo che le loro funzioni campione x(t)
e y(t) siano legate deterministicamente attraverso la trasformazione lineare:
y t H x t
(3.58)
dove ℋ è un operatore lineare, tempo-invariante, causale e asintoticamente stabile. La funzione x(t)
è della ingresso (o input, o eccitazione); la funzione y(t) è detta uscita (o output, o risposta).
L’operatore ℋ è lineare se, per ogni coppia di funzioni x(t) e y(t) e per ogni coppia di costanti
a e b in ℝ, vale la relazione:
H a x t b y t aH x t bH y t
(3.59)
L’operatore ℋ è tempo-invariante se, per ogni τ in , vale la relazione:
y t H x t
(3.60)
L’operatore ℋ è detto causale se la risposta y(t) dipende soltanto dal passato dell’eccitazione x()
con ≤ t.
L’ operatore ℋ è detto (asintoticamente) stabile se, per ogni ingresso limitato x(t) fornisce un’uscita
limitata y(t).
La risposta a regime (lontano dalle condizioni iniziali) dell’operatore (3.58) può essere espressa
attraverso l’integrale di convoluzione:
t
y t h t x d
(3.61)
0
dove h è detta funzione di risposta a impulso e pesa l’eccitazione applicata al tempo in funzione
del tempo trascorso (t - ). L’operatore ℋ è tempo-invariante se h non dipende esplicitamente da t,
ma soltanto dalla differenza t - ; ℋ è causale su h(t - ) = 0 per > t (assegna peso nullo alle
eccitazioni future); ℋ è asintoticamente stabile se è assolutamente integrabile in .
Ipotizzando che l’istante iniziale di applicazione dell’eccitazione sia t = -, e sfruttando
l’ipotesi di causalità, la (3.61) può essere riscritta nella forma:
74
y t
h t x d h x t d
(3.62)
Applicando la trasformata di Fourier ad entrambi i membri della (3.62), si ottiene l’espressione nel
dominio della frequenza della trasformazione lineare:
y H x
(3.63)
dove x e y sono le trasformate di Fourier di x e y (che si suppone esistano) e H è la funzione di
risposta in frequenza (FRF) dell’operatore lineare ℋ. La funzione di risposta in frequenza è la
trasformata di Fourier della funzione di risposta a impulso.
Se x(t) e y(t) sono funzioni campione di due processi aleatori stazionari X(t) e Y(t), allora la (3.58)
può essere formalmente interpretata come una trasformazione lineare di processi stazionari
Y t H X t
(3.64)
In questo caso ha senso chiedersi se, conoscendo la rappresentazione probabilistica di X è possibile
valutare la rappresentazione probabilistica di Y. Come passo preliminare, il problema è affrontato
nell’Esempio 3.1 per il caso particolare dell’amplificatore ideale.
Esempio 3.1. Amplificatore ideale.
Sia X(t) un processo aleatorio stazionario a media nulla (X = 0) e sia Y(t) l’uscita
dell’amplificatore ideale ℋ.
Y t aX t
(3.65)
dove la costante a rappresenta il guadagno dell’amplificatore. Applicando le definizioni di
auto- e cross-covarianza, è immediato dimostrare le seguenti relazioni:
CYX aC XX
CYY a 2 C XX
(3.66)
YY YX XX
Inoltre, sfruttando le equazioni di Wiener-Kinchine:
SYX aS XX
SYX a 2 S XX
(3.67)
XY 1
In generale, quando un processo aleatorio X(t) a media nulla è applicato un operatore lineare ℋ la
situazione può essere idealizzata come mostrato nello schema di Figura 3-7. Dal processo X(t) si
estrae una realizzazione x(t) che viene finestrata sul periodo T, ottenendo xT, quindi trasformata nel
dominio della frequenza ottenendo xT . Applicando la (3.63) si perviene alla risposta yT che
antitrasformata produce yT e quindi y, passando al linite per T→; quest’ultima è interpretata come
75
una realizzazione di Y. Analogamente xT e yT sono interpretate come realizzazioni dei processi
aleatori X T e YT che sono dunque legati dalla relazione formale:
YT H X T
(3.68)
Sostituendo la (3.68) nelle definizioni di densità di potenza spettrale e densità di potenza spettrale
incrociata si dimostra:
SYX H S XX
S XY H * S XX
(3.69)
SYY H S XX
2
Dalla definizione di coerenza di dimostra inoltre che:
XY
H
(3.70)
H
da cui emerge che la coerenza fra l’eccitazione e la risposta di un operatore lineare ha
necessariamente modulo unitario.
X t
x t
xT t
xT
h t x d
H xT
X T
YT
Y t
y t
yT t
yT
Figura 3-7. Schema per il calcolo della risposta stazionaria di sistemi lineari.
In generale, se l’ingresso X(t) ha media non nulla, allora il valore medio dell’uscita può essere
calcolato applicando l’operatore di media alla (3.62).
Y E Y t E h t X d
h t E X d
(3.71)
X
h d
X
H 0
La media dell’uscita è proporzionale alla media dell’ingresso attraverso il favore in zero della FRF.
Ne segue che se l’ingresso ha media nulla, allora anche l’uscita ha media nulla.
3.4.1 Derivazione di processi stazionari
L’introduzione del concetto di derivate di un processo aleatorio (così come per il concetto di
inegrale) richiederebbe la definizione del limite di un processo aleatorio (o del limite di una
successione di variabili aleatorie). In termini matematicamente approssimativi, è possibile
76
concepire la derivata X (t ) di un processo aleatorio X (t ) come il processo aleatorio le cui funzioni
campione x(t ) sono le derivate delle funzioni campione di X(t).
In altri termini, è possibile concepire la derivata temporale come un particolare operatore lineare
avente FRF H() = i. In quest’ottica, la densità di potenza spettrale del processo derivato può
essere ottenuta particolarizzando le (3.69):
S XX i S XX
S XX i S XX
(3.72)
S XX S XX
2
Le (3.72) possono essere facilmente generalizzate per considerare derivate di qualsiasi ordine n. In
questo caso l’auto-spettro della derivata n-ma di X è ottenuto nella forma:
S X n X n 2 n S XX
(3.73)
Dalle (3.72) discende che la coerenza fra un processo stazionario e la sua derivata risulta:
XX i sgn
(3.74)
cioè ha modulo unitario e fase /2. Questo è in accordo con il principio per cui la coerenza misura
la presenza di un legame lineare deterministico fra due processi aleatori.
Applicando le equazioni di Wieren-Kintchine alle (3.72) si ottengono relazioni analoghe per il
dominio del tempo:
d
C XX
d
d
C XX
d
d2
2 C XX
d
C XX
C XX
C XX
(3.75)
3.5 Momenti spettrali
La densità di Potenza spettrale unilaterale GXX () è definite dalla funzione (Figura 3-8):
GXX 2S XX
per 0
GXX 0
per 0
(3.76)
È una funzione non-negativa definite per 0 e possiede la seguente proprietà:
2X GXX ()d
0
(3.77)
77
Figura 3-8. Densità di Potenza spettrale bilatera e unilatera.
Si definiscono moment spettrali (o moment di Vanmarcke) le quantità:
X ,i i GXX ()d i 0,1, 2,...
(3.78)
0
In particolare, i primi 3 momenti spettrali risultano:
0
X ,0 GXX ()d S XX ()d 2X
0
X ,1 GXX ()d S XX ()d 0
0
(3.79)
X ,2 2GXX ()d 2 S XX ()d 2X
La posizione X,1 del baricentro dell’area sottesa da GXX() è data dalla relazione (Figura 3-9):
X ,1
G
G
0
0
XX
()d
XX () d
X ,1
(3.80)
X ,0
Il rapporto X = X,1 / 2 è detto frequenza attesa.
Il raggio di inerzia dell’area sottesa da GXX() è fornito dall’espressione:
1/2
X ,2
2G d
XX
0
G d
0 XX
X ,2
X ,0
X
X
(3.81)
Figura 3-9. Interpretazione geometrica dei moment spettrali.
78
Il raggio di inerzia dell’area sottesa da GXX() rispetto al suo baricentro, X,2 , fornisce una misura
della dispersione della potenza spettrale (Figura 3-9). Questa quantità è definita dalla relazione:
X ,2
2X ,1
1
X ,2
qX X ,2
X ,0
X ,0
(3.82)
Dove il parametro qX è detto ampiezza di banda:
qX 1
2X ,1
X ,0 X ,2
(3.83)
ed è una quantità adimensionale compresa fra 0 e 1.
3.6 Modelli di processi stazionari
Nel presente paragrafo sono presentati quattro classi di processi aleatori: il processo armonico, il
processo a banda stretta (narrow band), il processo a banda estesa (broad band) e il processo a
banda infinita (rumore bianco, white noise). Questi modelli così ordinati sono caratterizzati da
ampiezze di banda spettrale crescenti.
3.6.1 Processo armonico
Un processo aleatorio stazionario e a media nulla si definisce armonico se ogni sua possibile
realizzazione è esprimibile nella forma
x t A sin 0t y
(3.84)
dove l'angolo di fase y è una realizzazione della variabile aleatoria Y uniformemente distribuita
nell'intervallo 0, 2:
pY
1
2
0 2
(3.85)
79
Figura 3-10. Processo armonico: realizzazione (a), funzione di autocorrelazione (b), densità di Potenza spettrale (c).
La funzione di auto-covarianza coincide con la funzione di autocorrelazione e risulta
C XX E X t X t A2 sin 0t sin 0 t pY d
2 2
A
sin 0t sin 0 t d
2 0
A2
cos 0
2
(3.86)
La funzione densità di potenza spettrale di un processo armonico è definita come
S XX
1
A2
i
e CXX d ei cos 0 d
2
4
(3.87)
A2
0 0
4
i
2
Ne consegue che 2X A2 / 2 , inoltre X,i 0 A / 2 e la larghezza di banda vale q X 0 .
3.6.2 Processo a banda stretta
Un processo aleatorio stazionario e a media nulla si definisce a banda stretta se la sua densità di
potenza spettrale è non nulla solo entro un limitato range di frequenze con ampiezza B = 2 1 ,
dove B/ 0 0, 0 essendo il valor medio di banda: 0 1 2 / 2 .
Un processo a banda stretta si definisce ideale se la sua densità di potenza spettrale è definita come
80
S per 1 2
S XX 0
0 altrimenti
(3.88)
La varianza di X(t) è 2X 2S0 (2 1 ) .
Figura 3-11. Processo a banda stretta: realizzazione (a), funzione di autocorrelazione (b), densità di Potenza spettrale (c).
La funzione di auto-covarianza risulta
2
1
C XX S XX ei d 2 S0 cos d
B
sin 2
2 S0
cos
sin 2 sin 1 2 S0 B
0
B
2
(3.89)
Inoltre:
B2
B
B
X,2 2S0 B 02 ; q X
12
1202 B2 0 12
Ogni singola realizzazione del processo a banda stretta è caratterizzata da un contenuto armonico
concentrato intorno alla frequenza circolare al centro della banda armonica. Le realizzazioni
possono essere definite armoniche distorte, ovvero modulate in fase (fase non costante).
X,0 2S0 B ;
X,1 2S0 B0 ;
3.6.3 Processo a banda estesa
Un processo aleatorio stazionario si definisce a banda estesa se la sua densità di potenza spettrale è
non nulla solo entro un ampio range di frequenze. Un processo a banda estesa si definisce ideale se
la sua densità di potenza spettrale è definita come
81
S per B
S XX 0
0 altrimenti
(3.90)
La varianza risulta 2X 2S0 B .
Figura 3-12. Processo a banda estesa: realizzazione (a), funzione di autocorrelazione (b), densità di Potenza spettrale (c).
La funzione di auto-covarianza risulta
B
0
C XX S XX ei d 2 S0 cos d
sin B
2 S0 B
B
(3.91)
Inoltre:
2S0 B3
1
; qX
3
2
Ogni singola realizzazione del processo a banda estesa è caratterizzata da un andamento irregolare
dovuto all'ampiezza del suo contenuto armonico.
X,0 2S0 B ;
X,1 S0 B2 ;
X,2
3.6.4 Rumore bianco
Un processo aleatorio stazionario si definisce rumore bianco se la sua densità di potenza spettrale è
costante nell'intero range di frequenze; è generalmente indicato con il simbolo W(t):
S XX () S0
(3.92)
2
Risulta che X
82
Il processo a banda infinita è fisicamente non realizzabile ma la sua importanza in dinamica
strutturale è fondamentale.
Figura 3-13. Rumore bianco: realizzazione (a), funzione di autocorrelazione (b), densità di Potenza spettrale (c).
Fig. 17
La funzione di auto-covarianza risulta
CXX SXX eid S0 eid
2S0
(3.93)
E' immediato dimostrare che: X ,i i , qX 1 .
Ogni singola realizzazione di un processo definito rumore bianco è caratterizzata da un andamento
infinitamente irregolare dovuto all'infinito contenuto armonico.
4
Analisi statistica di processi aleatori stazionari
Nelle applicazioni pratiche le funzioni continue vengono discretizzate mediante sequenze ordinate
di numeri calcolati per un insieme definito di valori (non necessariamente equispaziati) assunti dalla
variabile indipendente. I segnali discreti sono pertanto definiti come funzioni di variabili
indipendenti che possono assumere solo un insieme finito di valori.
Chiamiamo x t una funzione della variabile continua t (generalmente il tempo) e xk la sequenza
degli N valori assunti da x agli istanti tk k 0,1,..., N 1 ; indichiamo inoltre con Tp la
lunghezza del segnale registrato e con Ts il periodo di campionamento, ovvero il tempo che
83
intercorre tra uno snapshot e il successivo (il pedice s deriva dalla parola inglese sample che
significa campione). Tali grandezze sono legate dalla relazione
Tp NTs
(3.94)
L'inverso del periodo di campionamento è definito frequenza di campionamento ns e vale
ns 1 Ts
(3.95)
mentre il reciproco della lunghezza del segnale campionato è definito risoluzione in frequenza n p e
corrisponde alla minima frequenza osservabile
n p 1 Tp
(3.96)
Il campionamento è il primo passo del processo di conversione di un segnale (funzione) da continuo
a discreto e la sua applicazione è vincolata al teorema del campionamento di Nyquist-Shannon, il
quale mette in relazione il contenuto del segnale originale con la frequenza ns . Il teorema afferma
che, sotto le opportune ipotesi, la minima frequenza di campionamento necessaria per evitare
ambiguità nella ricostruzione del segnale con larghezza di banda finita e nota è pari al doppio della
massima frequenza significativa, ovvero
ns 2nc
(3.97)
dove nc rappresenta la frequenza di cut-off. In altre parole, per campionare un segnale senza perdita
di informazione, bisogna campionarlo con frequenza almeno doppia rispetto alla frequenza della
massima componente spettrale del segnale originale (detta anche frequenza di Nyquist).
Un’armonica di frequenza maggiore di ns 2 viene campionata con meno di un punto per ogni
semi-periodo.
Aliasing e immagini….
Il teorema del campionamento viene anche utilizzato in analisi statistica per stabilire il numero di
esperimenti da eseguire per collezionare un numero di dati (campioni) sufficienti per poter
ricostruire correttamente una funzione non nota in alcuni punti, per esempio in punti inaccessibili a
causa di vincoli fisici oppure semplicemente per ottenere dati tra due punti campionati tramite un
esperimento. Congiuntamente a spline e a funzioni di regressione permette di eseguire analisi
elaborate su segnali di origine fisica (temperature, pressioni, conteggio di globuli bianchi e rossi,
conteggio di stelle...).
4.1
Analisi nel dominio del tempo - stima della funzione di autocorrelazione
4.2 Analisi nel dominio della frequenza - stima della funzione densità di potenza spettrale
La trasformata di Fourier di una funzione rispetto alla pulsazione è definita come
X
x t e
it
dt
(3.98)
congiuntamente l'anti-trasformata risulta
84
x t
X e
it
d
(3.99)
In questo modo le due funzioni x t e X sono legate dall'operatore trasformata di Fourier. In
ambito discreto ciò che lega i due vettori x e X è la trasformata discreta di Fourier o DFT; affinché
la trasformata sia invertibile le due sequenze devono avere la medesima lunghezza. La funzione
x t è di lunghezza finita e la si estende in maniera periodica per poterla rappresentare mediante
serie di Fourier
x t
Ae
j
i j t
(3.100)
j
dove j j p j 2n p j 2 Tp e A j sono i coefficienti di Fourier che valgono
Aj t
1
Tp
Tp
x t e
i j t
dt
(3.101)
0
La (3.100) è valida anche per la sequenza di valori discreti xk x tk dove tk kTs
xk
j
Aj e
i j tk
j
Aj e
i j kTs
j
i
Aj e
2
jkTs
Tp
Ae
j
j
i 2 jk / N
(3.102)
dove
1 N 1 2 ijk / N
xk e
N k 0
Aj
(3.103)
La sommatoria (3.102) è estesa comprendendo tutte le armoniche di frequenza n j jn p fino a
frequenza infinita. Se il segnale xk è campionato alla frequenza ns , per il teorema del
campionamento non possono essere distinte al suo interno armoniche con frequenza maggiore di
ns 2 .
Supponendo inizialmente che il segnale in questione non contenga armoniche superiori a ns 2 , la
(3.102) può essere riscritta nella forma
xk
N 2
j N 2
Aj ei 2 j / N
(3.104)
Definiamo DFT di xk la sequenza dei coefficienti di Fourier A j ordinati in modo da evitare indici
negativi e moltiplicati per il numero dei campioni N
NAj
xj
NAj N
j 0,1,..., N 2 1
j N 2, N 2 1,..., N 1
(3.105)
Sostituendo nella (3.104) si ottiene
85
xk
1 N 1
X j e2 ijk / N
N j 0
(3.106)
Si dimostra che la DFT definita in (3.106) è legata alla trasformata di Fourier continua dalla
relazione
X j ns X nj
(3.107)
cioè la DFT approssima la Trasformata di Fourier a meno di un fattore ns .
Nel caso in cui il segnale contenesse armoniche significative oltre la frequenza di cut-off la (3.107)
andrebbe sostituita con la seguente relazione:
X j ns X jn p mns
(3.108)
m
% stima PSDF
function [S, n] = psd1(x,Nwin,ns)
% stima PSD (monolatera normalizzata in frequenza) del segnale x campionato
% alla frequenza ns
% Nwin = lunghezza finestre per metodo di Welch (usare potenza di 2 per
% maggiore velocità)
Nfft = Nwin;
Nover = floor(Nwin/2);
Nt = length(x);
Nn = ceil(Nfft/2)+1;
S = zeros(Nn,1);
kk = 0;
i1 = 1;
i2 = Nwin;
while i2 <= Nt
kk = kk + 1;
X = fft(x(i1:i2),Nfft);
% fft: algoritmo ottimizzato per il calcolo
%
della DFT
S = S + X(1:Nn).*conj(X(1:Nn));
i1 = i1 + Nwin - Nover;
i2 = i2 + Nwin - Nover;
end
S = S / (kk * Nwin * ns/2);
n = (0:Nfft/2)*ns/Nfft;
Figura 4-1. Codice Matlab per stima Power Spectral Density Function mediante algoritmo fft.
86
5
Simulazione di processi aleatori
5.1 Metodo di Shinozuka
Il metodo di Shinozuka permette di simulare N realizzazioni x t di un processo aleatorio X t a
media nulla e con assegnata densità di potenza spettrale S x . Le x t sono espresse mediante
sovrapposizione di armoniche di ampiezze opportune e fasi casuali nella forma
N
x t 2 S x j cos j t j
(3.109)
j 1
dove j sono valori di frequenza distanti e j sono numeri aleatori uniformemente distribuiti
in 0, 2 .
Consideriamo la funzione z t definita in
:
N
i t
z t x t iy t 2 S x j e j j
(3.110)
j 1
dove risultano
x t Re z t
N
y t 2 S x j sin j t j
(3.111)
j 1
N
2 S x j cos j t j
2
j 1
Dalla (3.111) e dall'assunzione che j sono uniformemente distribuite si deduce che x t e y t
sono realizzazioni del medesimo processo aleatorio o, analogamente, che le due funzioni sono
realizzazioni di due processi X e Y con le medesime proprietà statistiche, ovvero
S x S y ,
Rx Ry
(3.112)
La funzione di autocorrelazione della z t a valori complessi sarà così definita
Rz E z t z t
E x t x t E y t y t iE x t y t iE y t x t
Rx Ry iE x t y t iE y t x t
(3.113)
2 Rx iE x t y t iE y t x t
Per la (3.110) la medesima funzione varrà anche
87
Rz E z t z t
N
i t
i t k
E 4 S x j S x k e j j e k
j ,k 1
N
4 S x j S x k e
i j t ik t
e
E e
i k j
(3.114)
j , k 1
L'ipotesi iniziale considerava j e k uniformemente distribuiti e statisticamente indipendenti per
k j , allora anche la loro differenza avrà distribuzione uniforme per k j , ovvero
E e
i k j
kj
(3.115)
Di conseguenza la (3.114) diventerà
N
Rz E z t z t 4 S x j eik
(3.116)
j 1
Ora è lecito eguagliare le parti reali della (3.113) e della (3.116)
N
2 Rx 4 Re S x j eik
j 1
N
j 1
2 S x ei d 4 S x j cos
0
(3.117)
N
S x cos d S x j cos
j 1
L'ultima uguaglianza della (3.117) non è altro che la definizione di integrale secondo Riemann; il
secondo membro converge al primo per 0 .
Il processo a media nulla x t simulato attraverso la(3.109) è stazionario ed ergodico; la sua
distribuzione tende ad essere Gaussiana (per N ) in virtù del teorema del limite centrale.
Una rappresentazione alternativa alla (3.109) che possiede migliore convergenza alla distribuzione
Normale è fornita dalla formula
N
i t
x t 2 Re S x j Aj e j
j 1
(3.118)
dove Aj R j iI j sono numeri complessi, non correlati, con distribuzione di probabilità Gaussiana
standardizzata N 0,1 .
88