Probabilità

Probabilità
Evento

Certo

Impossibile

Aleatorio
Evento è il termine che
indica un qualsiasi
avvenimento ben
determinato
che accade con certezza
che non può accadere
può accadere o meno in
modo casuale
Esempi
Supponiamo di avere un
barattolo contenente solo
palline nere.
L’evento “estraggo una pallina nera” è certo.
L’evento “estraggo una pallina gialla” è impossibile.
Esempi
Supponiamo di avere un
barattolo contenente
palline nere e rosse.
L’evento “estraggo una pallina nera” è aleatorio.
L’evento “estraggo una pallina rossa” è aleatorio.
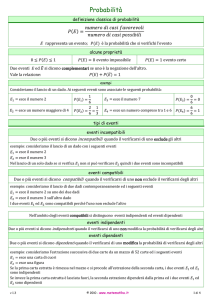
Definizione
La probabilità di un evento p(E) di un
evento E è data dal rapporto fra il
numero f di casi favorevoli ed il numero
complessivo n dei casi possibili.
In simboli:
f
p( E ) =
n
Esempio
Dato un barattolo con 4 palline
rosse e 5 palline blu: qual è la
probabilità di prendere una
pallina rossa?
Sono casi favorevoli tutti i casi in cui si
verifica l’evento: i casi favorevoli sono 4
 Sono casi possibili tutti i casi che possono
verificarsi: i casi possibili sono 9
 La probabilità è

Valori di probabilità

Probabilità di un evento
certo

Probabilità di un evento
impossibile

1
0
Probabilità di un evento
aleatorio
0<p<1
Eventi complementari
Due eventi si dicono complementari
quando il verificarsi del primo esclude il
verificarsi del secondo, ma sicuramente uno
dei due eventi si verificherà.
La somma di due eventi complementari è
sempre uguale a 1.
E’ il caso di un evento E ed il suo evento
contrario nonE.
nonE
p(E)+p(nonE)=1
E
Esempio
Dato un barattolo con 4 palline
rosse e 5 palline blu: qual è la
probabilità di prendere una
pallina rossa?
Evento E:
4
prendere una pallina rossa p( E ) = 9
 Evento contrario nonE:
5
non prendere una pallina rossa p(nonE ) =

9
Eventi incompatibili
Due eventi si dicono incompatibili quando il
verificarsi del primo esclude il verificarsi del
secondo, ovvero i due eventi non possono
verificarsi contemporaneamente.
Esempio
Considerando lancio di un dado:
“esca un numero pari” e “esca un
numero dispari” sono eventi
incompatibili.
Eventi compatibili
Due eventi si dicono compatibili quando il
verificarsi del primo non esclude il
verificarsi del secondo, ovvero i due eventi
si possono verificare contemporaneamente.
Esempio
Considerando lancio di un dado:
“esca un numero pari” e “esca un
numero minore di tre” sono eventi
compatibili.
Rappresentazione di eventi
compatibili e incompatibili
mediante gli insiemi
Eventi incompatibili
Eventi compatibili
Tipologie di eventi
Talvolta si richiede di calcolare la
probabilità di eventi semplici, altre volte di
eventi articolati. Così noi suddividiamo gli
eventi in tre tipi:
Evento semplice
Evento intersezione
Evento unione
Esempi
Consideriamo
20 dischetti uguali numerati da
1 a 20. Prendendo un solo dischetto avremo:
Evento semplice
Esce il numero 8
Esce un numero pari
Esce un numero con due cifre
Esce un multiplo di 3
Esempi
Evento intersezione
Esce un numero pari e multiplo di 3
Esce un numero dispari e minore di 10
Evento unione
Esce un numero pari o un multiplo di 3
 Esce un numero dispari o un numero
minore di 10
 Esce un multiplo di 6 o un numero minore
di 4
Probabilità di un evento semplice
Consideriamo 20 dischetti uguali numerati da
1 a 20. Voglio calcolare la probabilità dei
seguenti eventi semplici.
Esce
il numero 8
1
p=
20
(8)
Esce un numero pari
10
p=
(2, 4, 6, 8, 10, 12, 14, 16, 18, 20)
20
Esce un numero con due cifre
11
p=
(10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20)
20
Esce un multiplo di 3
6
p=
(3, 6, 9, 12, 15, 18)
20
Probabilità di un evento
intersezione
Consideriamo 20 dischetti uguali numerati da
1 a 20. Voglio calcolare la probabilità dei
seguenti eventi intersezione.
•
•
Esce un numero pari e multiplo di 3
(6, 12, 18)
p=
Esce un numero dispari e minore di 10
(1, 3, 5, 7, 9)
5
p=
20
3
20
Definizione
Dati i due eventi E1 ed E2,
il loro EVENTO INTERSEZIONE
(E1 ∩ E2)
è quell’evento che si verifica quando si
verificano contemporaneamente gli eventi
dati (E1 e E2)
I casi favorevoli sono rappresentati
dall’INTERSEZIONE dei casi favorevoli
Gli eventi intersezione possono essere considerati
come particolari combinazioni di due eventi
semplici, ovvero come la loro intersezione.
Esce un numero pari e multiplo di 3 = (6, 12, 18)
Esce un numero pari = (2, 4, 6, 8, 10, 12, 14, 16, 18, 20)
Esce un multiplo di 3 = (3, 6, 9, 12, 15, 18)
Esce un numero dispari e minore di 10 (1, 3, 5, 7, 9)
Esce un numero dispari = (1, 3, 5, 7, 9, 11, 13, 15, 17, 19)
Esce un numero minore di 10= (1, 2, 3, 4, 5, 6, 7, 8, 9)
Probabilità di un evento unione
Consideriamo 20 dischetti uguali numerati da
1 a 20. Voglio calcolare la probabilità dei
seguenti eventi unione.
Esce un numero pari o un multiplo di 3
(2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20)
•
Esce un numero dispari o un numero minore
di 10
(1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 19)
•
Esce un multiplo di 6 o un numero minore di
4
(1, 2, 3, 6, 12, 18)
•
13
p=
20
p=
14
20
6
p=
20
Definizione
Dati i due eventi E1 ed E2,
il loro EVENTO UNIONE
(E1 U E2)
è quell’evento che si verifica al verificarsi di
almeno uno degli eventi dati
(E1 o E2)
I casi favorevoli sono rappresentati
dall’UNIONE dei casi favorevoli
Per calcolare tale probabilità bisogna
individuare se gli eventi che compongono
l’evento unione, sono compatibili o
incompatibili, e quindi calcolare la loro
unione.
Eventi incompatibili
Eventi compatibili
Probabilità totale
La probabilità dell’evento unione viene
detta anche probabilità totale

La probabilità totale di eventi
incompatibili è data dalla somma delle
probabilità dei singoli eventi semplici

La probabilità totale di eventi compatibili
è data dalla somma delle probabilità dei
singoli eventi semplici meno la probabilità
del loro evento intersezione
Esce un numero pari o un multiplo di 3
f(numero pari) = (2, 4, 6, 8, 10, 12, 14, 16, 18, 20)
f(multiplo di 3) = (3, 6, 9, 12, 15, 18)
f(numero pari e multiplo di 3)= (6, 12 18) eventi compatibili
ftot =10+6-3=13; ntot=20
Esce un numero dispari o un numero minore di 10
f(numero dispari) = (1, 3, 5, 7, 9, 11, 13, 15, 17, 19)
f(numero minore di 10)= (1, 2, 3, 4, 5, 6, 7, 8, 9)
f(numero dispari e minore di 10)= (1, 3, 5, 7, 9) eventi compatibili
ftot =10+9-5=13; ntot=20
Esce un multiplo di 6 o un numero minore di 4
f(multiplo di 6)= (6, 12, 18)
f(minore di 4)= (1, 2, 3)
f(multiplo di 6 e minore di 4)= ( ) eventi incompatibili
ftot =3+3-0=6; ntot=20