TERNE DI RIFERIMENTO E ANGOLI CARATTERISTICI
Aerotecnica e impianti di bordo
Aerotecnica e impianti di bordo
Classe: 5^
Classe: 5^
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Terne di riferimento
Assi corpo
…
Asse corpo Y o asse
trasversale o asse
laterale
Y
Fisse
Mobili
hanno l’origine nel baricentro
del corpo e si muovono, quindi,
con esso
sono solidali ad un sistema
ritenuto immobile nello spazio
e nel tempo
(es. il suolo)
G
Asse corpo X o asse
longitudinale
TERNA CORPO
X
TERNA SUOLO
TERNA VENTO
Z
Aerotecnica e impianti di bordo
Classe: 5^
Sez.: ITIS CA
Asse corpo Z o asse
verticale
Aerotecnica e impianti di bordo
Modulo: 1 Cap.: 1
Classe: 5^
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Movimenti del velivolo attorno agli assi corpo
…
Assi vento
…
Y’
Asse vento Y’
Rollio (Roll)
• Alettoni
• Momento di rollio (MX)
• Stabilità laterale
G
Imbardata (Yaw)
• Timone di direzione
• Momento imbardante (MZ)
• Stabilità direzionale
V
X’
Z’
Asse vento X’
Beccheggio (Pitch)
• Elevatore
• Momento di beccheggio (MY)
• Stabilità longitudinale
Asse vento Z’
Aerotecnica e impianti di bordo
Aerotecnica e impianti di bordo
Classe: 5^
Classe: 5^
Sez.: ITIS CA
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Modulo: 1 Cap.: 1
Scomposizione della forza aerodinamica (F) secondo gli assi vento
Assi suolo
…
…
Portanza (P)
Asse suolo Z0
F
Y’
P
R
G
Z’
o
vo
l
Di
re
zio
ne
di
Devianza (D) o forza laterale
X’
Asse suolo X0
X0
Asse suolo Y0
Orizzonte
Resistenza (R)
D
V
Z0
Y0
Aerotecnica e impianti di bordo
Aerotecnica e impianti di bordo
Classe: 5^
Classe: 5^
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Equilibrio del velivolo lungo gli assi
…
Angoli caratteristici
nr. 6 gradi di libertà nello spazio
Tra gli assi corpo (X, Y, Z), assi vento (X’, Y’, Z’) e assi suolo (X0,
Y0, Z0) possono nascere degli angoli cosiddetti caratteristici in
quanto caratterizzano alcune fasi del volo. Questi angoli sono:
nr. 6 equazioni di equilibrio dinamico indipendenti
nr. 3 equazioni di equilibrio alle
rotazioni
attorno ai tre
assi di una terna presa come
riferimento
nr. 3 equazioni di equilibrio alle
traslazioni
lungo i tre
assi di una terna presa come
riferimento
Y
ANGOLO DI DERAPATA, DERIVA o DEVIAZIONE (δ
δ)
SMX = 0
SFY = 0
SMY = 0
G
SFZ = 0
ANGOLO DI SBANDAMENTO (θ)
MZ
MY
SFX = 0
ANGOLO DI INCIDENZA (α)
ANGOLO DI RAMPA (β
β)
SMZ = 0
X
MX
Z
Aerotecnica e impianti di bordo
Aerotecnica e impianti di bordo
Classe: 5^
Classe: 5^
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Sez.: ITIS CA
Angolo di bank o angolo di sbandamento (θ
θ)
Angolo di incidenza (a)
…
…
Angolo compreso tra X e X’
X
Angolo compreso tra Z = Z’ e Z0
G
a
X’
Modulo: 1 Cap.: 1
G
V
α>0
α<0
Portanza diretta nella direzione piedi-testa
Portanza diretta nella direzione testa-piedi
Z0
Aerotecnica e impianti di bordo
Aerotecnica e impianti di bordo
Classe: 5^
Classe: 5^
Sez.: ITIS CA
Modulo: 1 Cap.: 1
Sez.: ITIS CA
Angolo di derapata o angolo di deriva o angolo di deviazione (δ
δ)
…
θ
Z = Z’
θ>0
Virata destra
θ<0
Virata sinistra
Modulo: 1 Cap.: 1
Angolo di rampa (β
β)
…
Angolo compreso tra X’ e X0
Angolo compreso tra X e X’ = X0
X’
X
V
d
X’ = X0
G
β
X
d> 0
d< 0
Virata piatta destra
β>0
Velivolo in cabrata
Virata piatta sinistra
β<0
Velivolo in picchiata
TERNE DI RIFERIMENTO (fig 1)
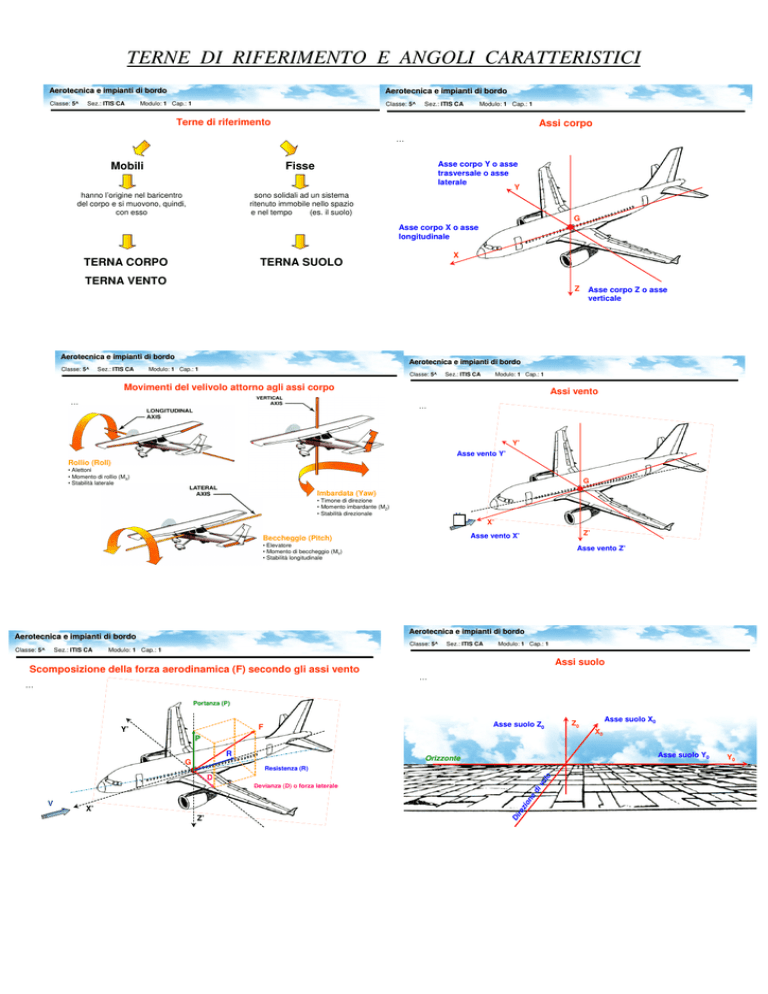
Nello studio della meccanica del volo vengono usati tre diversi sistemi cartesiani di riferimento: assi corpo, assi
vento e assi suolo. I primi due (assi corpo e assi vento) risultano esse mobili ovvero hanno sempre l’origine nel
baricentro del velivolo e si muovono con esso, mentre gli ultimi (assi suolo), sono fissi cioè solidali ad un sistema
(es. il suolo) ritenuto immobile nello spazio e nel tempo. La scelta dell’una o dell’altra terna dipende dal tipo di
problema che dovremo affrontare.
ASSI CORPO (fig. 2)
Il sistema di assi corpo è definito da un sistema di assi ortogonali (X, Y, Z) aventi la loro origine nel baricentro
(G) del velivolo. L’asse corpo X definito anche asse longitudinale:
è contenuto nel piano di simmetria del velivolo
è orientato positivamente verso la prua del velivolo
coincide con l’asse della fusoliera. In alcuni casi particolari, quando per esempio impiegato nei piani di
costruzione, questo asse può essere individuato anche dall’asse di rotazione dell’elica, o da una corda dell’ala,
ecc.
L’asse corpo Y definito anche asse trasversale o asse l aterale:
è normale al piano di simmetria del velivolo
è orientato positivamente verso la destra del pilota
coincide con l’asse dell’ala.
L’asse corpo Z definito anche asse verticale:
è contenuto nel piano di simmetria del velivolo
è orientato positivamente nel senso testa-piedi
è perpendicolare agli assi X e Y.
MOVIMENTO DEL VELIVOLO ATTORNO AGLI ASSI CORPO (fig. 3)
Qualunque manovra venga eseguita da un aereo durante il volo questa può essere ricondotta ad una
combinazione più o meno semplice di tre movimenti fondamentali che l’aeroplano può compiere attorno ai suoi
tre assi corpo: longitudinale (longitudinal axis), trasversale (lateral axis) e verticale (vertical axis).
I tre movimenti prendono il nome di:
Rollio (Roll) – E’ il movimento attorno all’asse longitudinale (X), e con il quale l’aereo si inclina alzando e
abbassando le semiali. Tale movimento si ottiene agendo sugli alettoni. Attorno all’asse longitudinale si
individua il momento di rollio (MX) e, come vedremo in seguito, la stabilità laterale.
Beccheggio (Pitch) – E’ il movimento attorno all’asse trasversale o laterale (Y), e con il quale l’aereo alza o
abbassa il muso. Tale movimento si ottiene agendo sull’elevatore. Attorno all’asse longitudinale si individua il
momento di beccheggio (MY) e, come vedremo in seguito, la stabilità longitudinale.
Imbardata (Yaw) – E’ il movimento attorno all’asse verticale (Z), e con il quale l’aereo sposta il muso verso
destra o verso sinistra si chiama imbardata (yaw). Tale movimento si ottiene agendo sul timone di direzione.
Attorno all’asse longitudinale si individua il momento di imbardata (MZ) e, come vedremo in seguito, la stabilità
direzionale.
ASSI VENTO (fig. 4)
Il sistema di assi vento è definito da un sistema di assi ortogonali (X’, Y’, Z’) aventi la loro origine nel baricentro
(G) del velivolo e la cui direzione dipende dalla direzione della velocità (V) del velivolo rispetto all’aria.
Attenzione! - La direzione del vento relativo non dipende dalla posizione del velivolo rispetto al terreno (assetto
cabrato o picchiato).
L’asse vento X’:
coincide con la traiettoria di volo del velivolo
è diretto secondo la direzione della velocità (V) del velivolo rispetto all’aria
è positivo nel senso del moto.
L’asse vento Y’:
è perpendicolare all’asse X’
è positivo verso destra.
L’asse vento Z’:
è perpendicolare agli assi X’ e Y’
è positivo verso il basso.
SCOMPOSIZIONE DELLA FORZA AERODINAMICA (F) SECONDO FLI ASSI VENTO (fig. 5)
La risultante (F) delle forze aerodinamiche agenti sul velivolo viene generalmente scomposta nello spazio
secondo le sue tre componenti e prendendo come riferimento gli assi vento essendo, sia le forze che questi assi
legati alla velocità relativa aeroplano-aria.
Le tre componenti della forza aerodinamica F sono:
portanza P: è la componente della forza aerodinamica secondo l’asse Z’, la cui espressione matematica è:
P = ½ ρ V2 S C P
resistenza R: è la componente della forza aerodinamica secondo l’asse X’, la cui espressione è:
R = ½ ρ V2 S C R
devianza D (o forza laterale): è la comp. della forza aerodinamica secondo l’asse Y’, la cui espressione è:
D = ½ ρ V2 S C D
ASSI SUOLO (fig. 6)
Il sistema di assi suolo (X0, Y0, Z0) è un sistema fisso il cui piano individuato dagli assi X0 e Y0 coincide con la
superficie terrestre.
L’asse suolo Y0:
• è contenuto in un piano tangente alla superficie media della terra;
• è parallelo all’orizzonte apparente;
• è orientato positivamente verso la destra di un osservatore che guarda lungo la direzione positiva dell'asse X0
(direzione del moto).
L’asse suolo X0:
• è contenuto in un piano tangente alla superficie media della terra;
• è orientato positivamente in avanti ovvero verso la direzione del moto.
L’asse suolo Z0:
• è perpendicolare a X0 e Y0;
• è orientato positivamente verso l’alto.
EQUILIOBRIO DEL VELIVOLO LUNGO GLI ASSI (fig. 7)
Negli studi di meccanica del volo, il velivolo viene sempre considerato come un corpo libero nello spazio,
supposto rigido (indeformabile) ed a comandi bloccati (superfici di governo non libere di muoversi intorno al
proprio asse di cerniera, ma fisse in una determinata posizione). In queste condizioni l’aeromobile è
caratterizzato da sei gradi di libertà; per definirne univocamente il moto, quindi, occorrono sei equazioni di
equilibrio dinamico indipendenti. Di queste equazioni, tre devono esprimere gli equilibri alle traslazioni lungo i
tre assi di una terna presa come riferimento e le altre gli equilibri alle rotazioni intorno agli stessi assi.
Esprimendo matematicamente queste sei equazioni otterremo:
FX = 0 ; FY = 0 ; FZ = 0
MX = 0 ; MY = 0 ; MZ = 0
ANGOLI CARATTERISTICI (fig. 8)
Tra gli assi corpo (X, Y, Z), assi vento (X’, Y’, Z’) e assi suolo (X0, Y0, Z0) possono nascere degli angoli
cosiddetti angoli caratteristici in quanto caratterizzano alcune fasi del volo. Questi angoli sono:
Angolo di incidenza (a): è l’angolo compreso tra X e X’
Angolo di sbandamento o angolo di bank (q): è l’angolo compreso tra Z = Z’ e Z0
Angolo di derapata o di deriva o di deviazione (d): è l’angolo compreso tra X e X’ = X0
Angolo di rampa (ß): è l’angolo compreso tra X’ e X0.
ANGOLO DI INCIDENZA (α
α) (fig. 9)
E’ l’angolo contenuto nel piano di simmetria del velivolo e che l'asse corpo longitudinale X forma con l’asse vento
longitudinale X’; assunto positivo se è tale da dar luogo ad una portanza diretta nel senso piedi-testa del pilota.
ANGOLO DI BANK O ANGOLO DI SBANDAMENTO (θ
θ) (fig. 10)
E’ l’angolo contenuto nel piano normale a X e che l'asse corpo verticale Z, coincidente con l’asse vento Z’, forma
con l’asse suolo Z0; assunto positivo se la semiala destra risulta più bassa della sinistra; con tale convenzione lo
sbandamento risulta positivo se la virata è destra.
ANGOLO DI DERAPATA O DI DERIVA O DI DEVIAZIONE (δ) (fig. 11)
E’ l’angolo contenuto nel piano orizzontale del velivolo e che l'asse corpo longitudinale X forma con l’asse vento
X’, coincidente con l’asse suolo X0; assunto positivo se il vento relativo (V) batte sul lato sinistro dell’aeromobile
e la semiala destra risulta più indietro rispetto alla semiala sinistra; con tale convenzione la derapata risulta
positiva se, ad esempio, la virata piatta è destra.
ANGOLO DI RAMPA (β) (fig. 12)
E’ l’angolo che l’asse vento X’ forma con l’asse suolo X0; per convenzione l’angolo è positivo se il velivolo sta
cabrando, negativo se sta picchiando.