Piano cartesiano - SCUOLA SECONDARIA DI I GRADO “G.PASCOLI”

IL PIANO CARTESIANO
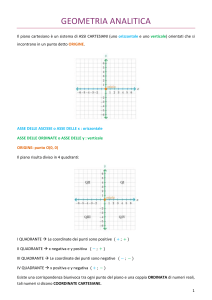
Se si considerano due rette orientate perpendicolari tra loro (dette assi cartesiani)
si ottiene un sistema di assi cartesiani ortogonali, che si intersecano in un punto O
detto origine.
La retta orizzontale prende il nome di asse delle x o delle ascisse mentre quella
verticale è l’asse delle y o delle ordinate.
Tali rette dividono il piano in quattro parti dette quadranti
Fissata un’unità di misura e riportata sugli assi, se da un qualsiasi punto del piano
conduciamo le perpendicolari all’asse x e all’asse y, otteniamo rispettivamente
ascissa e ordinata del punto che costituiscono le coordinate di tale punto.
Distanza tra due punti A e B aventi la
stessa x :
AB = │yA - yB │
A(+3;+5) e B(+3;-2)
AB = │yA - yB │=│+5-(-2)│=│+5+2 │= 7
Distanza tra due punti A e B aventi la
stessa y :
AB = │ xA – xB │
A(-4;-1) e B(+2;-1)
AB =│xA – xB │= │-4-(+2)│ =│-4-2 │= 6
Distanza tra due punti con coordinate
diverse :
A(+1;-4) e B(-3;-1)
AB =
2
( xA − xB ) + ( yA − yB )
2
AB =
=
2
( xA − xB ) + ( yA − yB )
2
=
[+1 − (−3) ] + [−4 − (−1) ] =
2
2
2
2
= (+1+ 3) + ( −4 +1) =
€
2
€
€
2
= (+4 ) + ( −3) =
+16 + 9 = 25 = 5
ALGEBRA 12
€
€
€
€
Punto medio di un segmento AB :
A(-2;-4) e B(-4;+8)
⎛ −2 + ( −4 ) −4 + (+8) ⎞ ⎛ −2 − 4 −4 + 8 ⎞
M ⎜
;
;
⎟ =
⎟ = ⎜
2
2
2 ⎠
⎝
⎠ ⎝ 2
⎛ x + x B y A + y B ⎞
M ⎜ A
;
⎟
⎝ 2
2 ⎠
€
= ( −3;+2)
€
ALGEBRA 13