LUOGHI GEOMETRICI
Ricordiamo che il luogo geometrico è un insieme di punti che godono di una determinata
proprietà. I più noti luoghi geometrici sono: la circonferenza, l'asse di un segmento, la
bisettrice di un angolo.
• Luogo dei punti del piano equidistanti dagli estremi del segmento AB .
Se A( x1 ; y1 ) e B( x2 ; y2 ) sono gli estremi del segmento e P( x; y ) il generico punto
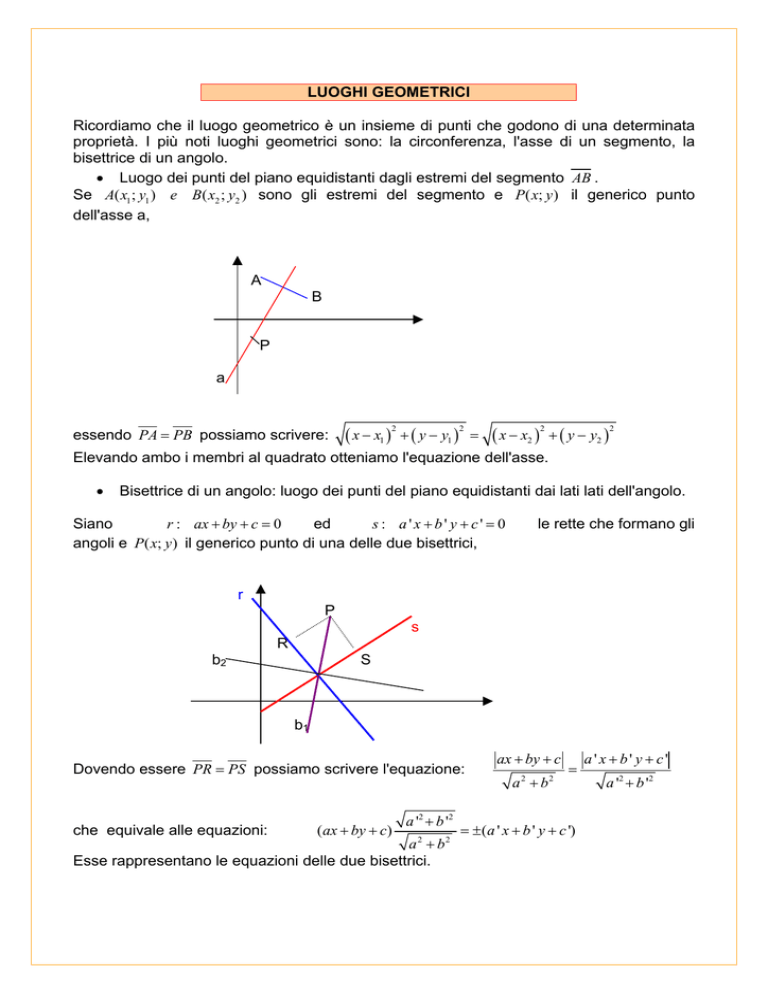
dell'asse a,
A
B
P
a
essendo PA = PB possiamo scrivere:
( x − x1 ) + ( y − y1 )
2
2
=
( x − x2 ) + ( y − y2 )
2
2
Elevando ambo i membri al quadrato otteniamo l'equazione dell'asse.
•
Bisettrice di un angolo: luogo dei punti del piano equidistanti dai lati lati dell'angolo.
Siano
r : ax + by + c = 0
ed
s : a'x +b' y + c' = 0
angoli e P( x; y ) il generico punto di una delle due bisettrici,
le rette che formano gli
r
P
s
R
b2
S
b1
Dovendo essere PR = PS possiamo scrivere l'equazione:
che equivale alle equazioni:
(ax + by + c)
a '2 + b ' 2
a 2 + b2
Esse rappresentano le equazioni delle due bisettrici.
ax + by + c
a 2 + b2
=
= ± (a ' x + b ' y + c ')
a'x +b' y + c'
a '2 + b ' 2
•
Luoghi geometrici dipendenti da un parametro
Consideriamo questo caso facendo riferimento al seguente esercizio:
Data la circonferenza
γ : x2 + y 2 − 2x − 3 = 0
determinare il luogo descritto dal
punto medio M della generica corda passante per l'origine.
A
B
x2 + y 2 − 2 x − 3 = 0
Per deteminare i punti A e B consideriamo il sistema:
y = mx
e ricaviamo (1 + m 2 ) x 2 − 2 x − 3 = 0 da cui
1± ∆
1 + m2
1± ∆
y = m
2
1+ m
x=
∆
= 4 + 3m 2
4
1 1+ ∆ 1− ∆
+
xM =
2 1 + m 2 1 + m 2
Il punto medio M della generica corda avrà coordinate:
1 1+ ∆ 1− ∆
y = 2 m 1 + m 2 + 1 + m 2
1
x=
1 + m2
Le equazioni parametriche del luogo sono quindi:
m
y=
1 + m2
Ricavando il parametro m dalla prima e sostituendo nella seconda otteniamo l'equazione
algebrica del luogo:
x2 + y 2 − x = 0 .












