1. Un sistema elettrostatico a simmetria sferica è costi
di carica Q, racchiuso in un guscio dielettrico di costa
contenuta in un guscio conduttore di raggio interno c
tuttoSAPIENZA"
lo spazio interno al guscio conduttore.
UNIVERSITA' DEGLI STUDI di ROMA in
"LA
Anno Accademico 2012 – 2013 – Ing. Aerospaziale
Esame di Elettromagnetismo (ord. 509, 6 CFU)
Prova scritta del 20 Giugno 2013
(Esercizi A: 6 punti ciascuno,
A1)
FACOLTA’ DI INGEGNERIA – UNIVERSITA’ DI ROMA “LA SAPIENZA”
DI FISICA GENERALE II – 17 FEBBRAIO 2003
quesiti B:ESAME
4 puntiSCRITTO
ciascuno)
a
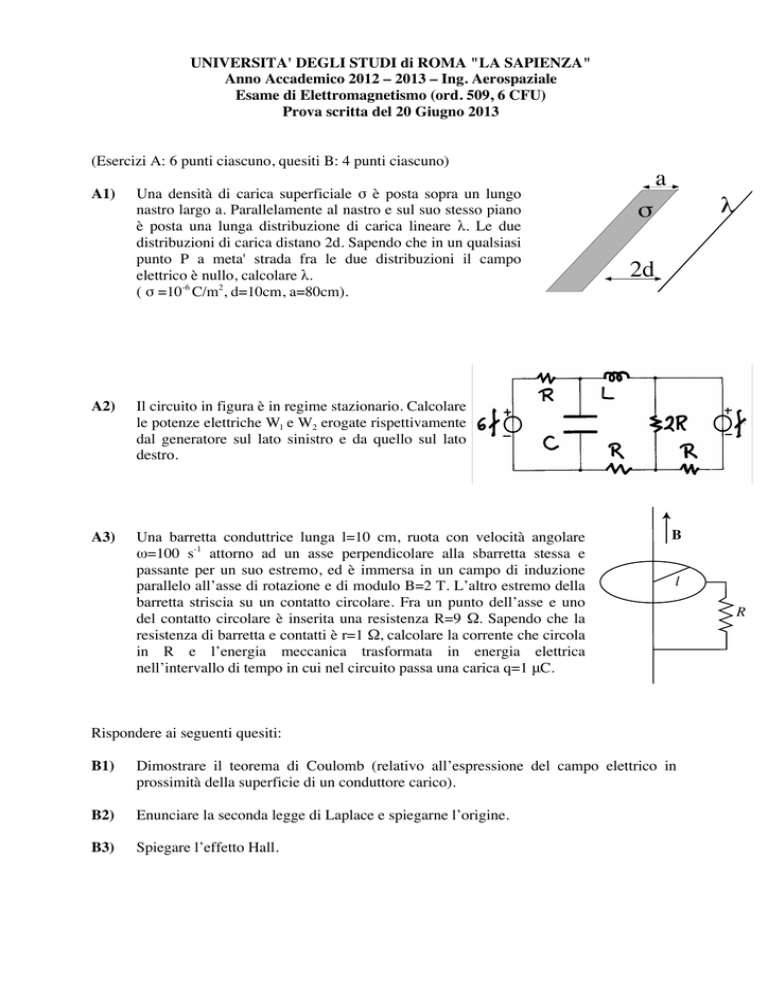
Una densità di carica 1)
superficiale
posta superficiale
sopra un σlungo
Una densita'σ diè carica
e' posta
λ
nastro largo a. Parallelamente
e sullargo
suoa.stesso
piano al
sopra al
un nastro
lungo nastro
Parallelamente
σ
2.LeUna
lamina conduttrice rettangolare è parzialme
nastro e sul
stessolineare
piano e' λ.
posta
una
lunga
è posta una lunga distribuzione
di suo
carica
due
un'altra
distribuzione
di carica
lineare
λ. Le lamina
due conduttrice piegata ad U, di pari larghe
distribuzioni di carica distano
2d. Sapendo
che in
un qualsiasi
distribuzioni di carica distano 2d.lembi
Sapendo
cheseconda rispettivamente a=1cm e b=2cm
della
punto P a meta' strada infraun le
due punto
distribuzioni
il campo
4 le due
qualsiasi
P a meta' strada
f=10fra
V è inserito tra i due2d
conduttori. Calcolare la
elettrico è nullo, calcolaredistribuzioni
λ.
il campo elettrico e' nullo,
elettrica agente sulla lamina centrale in situazione elet
calcolare λ . ( σ =10-6C/m2, d=10cm,a=80cm)
( σ =10-6 C/m2, d=10cm, a=80cm).
2) Nel circuito in figura l'interruttore3.viene
chiuso in figura è in regime stazionario. Calcol
Il circuito
a t=0. Calcolare l'energia immagazzinata
dal generatore sul lato sinistro e da qu
nell'induttanza nell'istante in cui sirispettivamente
eguagliano le
L
tensioni ai capi dell'induttanza e della
resistenza.
(L=0.5 mH, R=500 Ω,f=200 V)
R
f
A2)
Il circuito in figura è in regime stazionario. Calcolare
le potenze elettriche Wl e W2 erogate rispettivamente
Una sbarretta
dal generatore sul lato3)sinistro
e da isolante
quellocon
suldensita'
lato di carica λ ruota
nel piano (x,y) in senso orario intorno all'asse z ,
destro.
con velocita' angolare ω costante, e con
z
l
un'estremita' incernierata nell'origine. Ricavare
modulo, direzione e verso del momento magnetico
generato dalla sbarretta.
A3)
λ
4. L'avvolgimento di un solenoide ideale, di densità n
Una barretta conduttrice
lunga
l=10 cm, rappresentata
ruota constazionaria
velocità
angolare
4) La
spira rettangolare
in
figura e' posta
I=10A. All'interno del B
solenoide, parall
-1
nel
piano
(x,y)
a
distanza
d
da
un
lungo
filo
sottile
ω=100 s attorno ad un asse perpendicolare alla materiale
sbarrettaferromagnetico,
stessa e I(t)
di sezione costante
a e Sperme
posto lungo l'asse y e percorso da una corrente
passante per un suo estremo,
ed è immersa in un campo
di induzione
la
densità
di
corrente
di
magnetizzazione
Jm sulla
variabile I(t)=α t. Ricavare modulo, direzione e
l
parallelo all’asse di rotazione
e
di
modulo
B=2
T.
L’altro
estremo
della
direzione
e
il
verso.
verso della forza che subisce nel tempo la spira se
h
barretta striscia su un contatto
Fra unR punto
dell’asse
presentacircolare.
una resistenza
al passaggio
dellae uno d
R
corrente.una resistenza R=9 Ω. Sapendo che la
del contatto circolare è inserita
5. Un 'onda elettromagnetica piana si propaga progres
resistenza di barretta e contatti è r=1 Ω, calcolare la corrente
circola
cartesianoche
nella
cui origine è posta una spira circo
in R e l’energia meccanica trasformata in induttanza
energia trascurabile.
elettrica Disponendo la spira con il ve
in figura
un fascio
di luce
collimato
nell’intervallo di tempo5)inNell'apparato
cui nel circuito
passa
una carica
q=1
μC.
con
quello
dell'asse
z, si misura una corrente sinusoid
Rispondere ai seguenti quesiti:
parte dall'origine O con un angolo α = 45o verso
osserva invece passaggio di corrente se si dispone la
uno specchio piano sovrastante, parallelo al piano
dell'asse
y. Calcolare il rapporto tra ragg
(x,y). Dopo la riflessione la luce con
incidequello
sull'asse
x
radiazione
e scrivere l'espressione dei campi E e B
nel punto x0=20 cm. Se davanti allo
specchio viene
posta una lastra di vetro di indice
di rifrazione
numero
d'onda e la pulsazione in funzione di a, R, I0,
n1=1.5 e spessore d la luce incide sull'asse x nel
punto x1=18.5 cm .Calcolare lo spessore della
0
dilastra.
Coulomb (relativo all’espressione del campo elettrico in
B1)
Dimostrare il teorema
prossimità della superficie di un conduttore carico).
B2)
Enunciare la seconda legge di Laplace e spiegarne l’origine.
B3)
Spiegare l’effetto Hall.
o α
x
x
UNIVERSITA' DEGLI STUDI di ROMA "LA SAPIENZA"
Anno Accademico 2011 – 2012 – Ing. Aerospaziale
Esame di Fisica II (ord. 270, 9 CFU)
Prova scritta del 20 Giugno 2013
FACOLTA’ DI INGEGNERIA – UNIVERSITA’ DI ROMA “LA SAPIENZA”
DI FISICA GENERALE II – 17 FEBBRAIO 2003
(Esercizi A: 6 punti ciascuno, quesiti B:ESAME
3 puntiSCRITTO
ciascuno)
2. Una lamina conduttrice rettangolare è parzialm
A1)
a
un'altra lamina conduttrice piegata ad U, di pari larg
Una densità di carica superficiale
σ è di
posta
sopra
un lungo
1) Una densita'
carica
superficiale
σ e'nastro
posta
lembi
della largo
seconda rispettivamente a=1cm e b=2
λ
a. Parallelamente al nastro
e sul
suo nastro
stessolargo
piano
è posta
sopra
un lungo
a. Parallelamente
f=104 una
V al
è lunga
inserito tra i dueσconduttori. Calcolare
nastroλ.e sul
piano e' posta
una
lunga
distribuzione di carica lineare
Le suo
duestesso
distribuzioni
dielettrica
carica
distano
agente
sulla lamina centrale in situazione el
distribuzione
di
carica
lineare
λ.
Le
due
2d. Sapendo che in un qualsiasi punto P a meta' strada fra le due
distribuzioni di carica distano 2d. Sapendo che
distribuzioni il campo elettrico
è nullo, calcolare λ.
in un qualsiasi punto P a meta' strada fra le due
-6
2
( σ =10 C/m , d=10cm, a=80cm).
distribuzioni il campo elettrico 3. e'Il circuito
nullo, in figura è in 2d
regime stazionario. Calc
calcolare λ . ( σ =10-6C/m2, d=10cm,a=80cm)
rispettivamente dal generatore sul lato sinistro e da q
A2)
2) Nel circuito in figura l'interruttore viene chiuso
R
Il circuito in figura è in regime
Calcolare
a t=0. stazionario.
Calcolare l'energia
immagazzinata
in cui si eguagliano le
le potenze elettriche Wl enell'induttanza
W2 erogatenell'istante
rispettivamente
tensioni ai capi dell'induttanza e della
dal generatore sul lato sinistro
e da quello sul lato
resistenza.
destro.
(L=0.5 mH, R=500 Ω,f=200 V)
L
f
z
A3)
3) Una sbarretta isolante con densita' di carica λ ruota
nel piano (x,y) in senso orario intorno all'asse z ,
Una barretta conduttrice con
lungavelocita'
l=10 cm,
ruota con velocità angolare
angolare ω costante, e con
ω=100 s-1 attorno ad unun'estremita'
asse perpendicolare
alla sbarretta
stessa edi un solenoide B
4. L'avvolgimento
ideale, di densità
incernierata nell'origine.
Ricavare
modulo,
e verso
magnetico
passante per un suo estremo,
ed direzione
è immersa
in del
unmomento
campo
di induzione
stazionaria
I=10A. All'interno del solenoide, para
generato
sbarretta.
parallelo all’asse di rotazione
e didalla
modulo
B=2 T. L’altro
estremo
della
materiale
ferromagnetico,
di sezione costante e perm
l
l
λ
barretta striscia su un contatto circolare. Fra un puntola dell’asse
uno
densità die corrente
di magnetizzazione JmS su
del contatto circolare è4)inserita
resistenza
R=9 Ω.
Sapendo
la
e ilche
verso.
La spira una
rettangolare
rappresentata
indirezione
figura
e' posta
R
nel
piano
(x,y)
a
distanza
d
da
un
lungo
filo
sottile
resistenza di barretta e contatti è r=1 Ω, calcolare la corrente che circola I(t)
a
posto lungo l'asse y e percorso da una corrente
in R e l’energia meccanica
trasformata in energia
5. Un 'ondaelettrica
elettromagnetica piana si propaga progre
variabile I(t)=α t. Ricavare modulo, direzione e
nell’intervallo di tempo inverso
cui nel
una
q=1
μC.
cartesiano
nella
dellacircuito
forza chepassa
subisce
nelcarica
tempo
la
spira
se cui origine è posta una spira
h circ
d
induttanzadella
trascurabile. Disponendo la spira con il
presenta una resistenza R al passaggio
corrente.
con quello dell'asse z, si misura una corrente sinuso
A4)
Un'onda elettromagnetica piana si propaga progressivamente
lungo
l'asse di
x corrente
di un se si dispone
osserva invece
passaggio
con circolare
quello dell'asse
y. Calcolare
riferimento cartesiano nella cui origine è posta una spira
di raggio
a=10cm,il rapporto tra ra
5) Nell'apparato
in Disponendo
figura un fascioladiradiazione
luce collimato
resistenza R e induttanza
trascurabile.
spira
con eil scrivere
versore l'espressione
normale di dei campi E e
o
parte quello
dall'origine
O con un
α = 45una
verso
numero
d'onda
e la pulsazione
in funzione di a, R, I0
riferimento coincidente con
dell'asse
z, angolo
si misura
corrente
sinusoidale
uno specchio piano sovrastante, parallelo al piano
I(t)=I0 sin(2πνt), con ν=108Hz.
Non si osserva invece passaggio di corrente se si
(x,y). Dopo la riflessione la luce incide sull'asse x
dispone la spira con il versore
normale
coincidente
conspecchio
quelloviene
dell'asse y. Calcolare il
nel punto x0=20 cm.
Se davanti allo
posta
una
lastra
di
vetro
di
indice
di
rifrazione
rapporto tra raggio della spira e lunghezza d'onda della radiazione e scrivere
e spessoreesprimendo
d la luce incide
sull'asse x nel
l'espressione dei campi E en1=1.5
B dell'onda,
le ampiezze,
il numero d'onda e la x
punto x1=18.5 cm .Calcolare lo spessore della
0
x
pulsazione in funzione di a,
R, I , ν.
o α
lastra. 0
Rispondere ai seguenti quesiti:
B1)
Enunciare la seconda legge di Laplace e spiegarne l’origine.
B2)
Spiegare l’effetto Hall.
1
1 Q(r)
1
Soluzioni
della prova
In simmetria
sferica:scritta
Dr (r) = del 17 Febbraio
→ Er (r)2005
=
Q(r)
4π
4πεr ε0 r 2
"
#
! c
dr
Q
1
1
Q
1 −Q(r)
1 Q(r)
=
−
b ≤ r ≤ c : V (r)
V (c) =
2 = 4πε
In simmetria sferica: Dr (r) =
→
E
(r)
4πε
r
r 2c
r
0
0
r
2
Soluzioni
4π r
"
# 4πεr ε0 !r b
! cQ 1 1 "
Q #
dr
1
a ≤ r ≤ b : V (r) − V (b) = VQ(r) − dr
−Q =1
→
4πε20 =b c
4πε
− r ε0 r r 2
b ≤ r ≤ c : V (r) − V (c) =
4πε0 "r r # 4πε0 "
r
c #
Q " 1 1#
Q
1! 1
→ V (r) = Q
A1)
1 −1 + Q0 b − bcdr dl
a ≤ r ≤ b : V (r) − V (b) = V (r) − 4πεr ε0 r− b = 4πε
→
"
#
" r #
R
4πε0 b
c Q 4πε1r ε0 1 r r 2 Q
1 1
"
r ≤ a : V (r) − V (a) = 0" → V#(r) =
−# +
−
4πεr ε01 a 1 b
4πε0 b c
Q
Q
1 1
O
→ V (r) =
−
+
−
4πε
ε
r
b
4πε
b
c
r
0
0
2
z
"
#
"
##
"
#
"
#
Q
1
1
Q
1
1
f
2
#x
d =10 →2 V (r)f=
d
#x
dU−v V (a)
r ≤ a :F =
V (r)
−
+
− a d
=
CP ∆V
=
εr0ε0 +aε0 b = 4πε0 b
+
x
4πε
c
dx
dx 2
2 dx
a
b
∆V
r2
1
/
/
2
b
108 · 8.8 10−12 · 1 · 3 10−2
f 2 ε0 #(a + b)
−1
#
=
=
=
"
#
"
#0.66 10 N f
0
2ab
2
2· 1 10−2 · 2 10−2
f d
#x
d 1
#x
dUv
a
=
CP ∆V 2
=
ε0 + ε0
=
Fx = +
A2) 2
dx 3 dx
2
dx
a
b
∆V
b
Il circuito equivalente
in situazione
R
8
−12
−2 stazionaria è
2
· 8.8 10
· 1 · 3 10
f ε0 #(a
+ b) in 10
mostrato
= figura.
= 0.66 10−1 N
=
−2
−2
0
2ab
2 · 1 10 · 2 $10
$
+
6f = 4RI1 − 2RI2
3f /R = 2I1 − I2
I1
6f
−f = −2RI1 + 3RI2
f /R = 2I1 + 3I2
3
Il circuito
mostrato in
$
6f =
−f =
equivalente
→ 2I1 −I2 =in6I1situazione
−9I2 →
figura.
f
f
I2 = $
e I1 = 2
R
R
4RI1 − 2RI2
3f /R
−2RI
f /R
1 + 3RI2
A3)
R
stazionaria
8I
→ è I1 = 2I2
2 = 4I1
→
2I1 −I2 = 6I1 −9I2
→
= 2I1 − I2
= 2I1 + 3I2
5
→
I1
6f
S
J%m
f
f
W1 = 6f · 2 = 12
R
R
+
I2
2R
2R
I1 = 2I2
aν
1
a
=
$
λ
c
30
4
x
R
S
3
4 R
Jm
= M = χm H = χm nI = (µr − 1) nI = 4·10
2 ·10 = 4 10 A/m
f
f
I2 =
e I1 = 2
R
R
S
Jm
8I2 = 4I1
x
f
f2
f
f2
W1 = 6f · 2 = 12
e W2 = −f · = −
R
R+
R
R
4
5
P
R
I2
+
f
n̂
R
%
f
f2
M
e W2 = −f · = −
µr
R
R
ω = 2πν
k=
2πν
c
S
J%m
n̂
z
dΦ
dBz
dBz
RI0
2
3
4
=−
·−
πa1)=
sin (ωt)
= M = χm H =−χdt
= (µ
nIRI(t)
= 4·10→·10 =
4=
10− A/m
m nI
%
dt r
dt
πa2
M
µr
RI0
Bz (t) = 2 cos (ωt)
πa ω
Onda:
A4)
cRI0
aν RI0 1
2πν
% = ẑBza =
B
Bz = $2 cos (kxω−=ωt)
2πν
kE%== ŷEy Ey = 2 cos (kx − ωt)
πa ω
λ
c πa ω30
c
Onda:
dΦ
dBz
dBz
RI0
−
=−
· πa2 = RI(t) →
= − 2 sin (ωt)
dt
dt
dt
πa
RI0
Bz (t) = 2 cos (ωt)
πa ω
% = ẑBz
B
Bz =
RI0
cos (kx − ωt)
πa2 ω
f
% = ŷEy
E
Ey =
y
x
z
y
x
cRI0
cos (kx − ωt)
πa2 ω











