esercitazione 3

TEMA D’ESAME DEL 04-05-2012
Il docente di Probabilità e Statistica, per verificare la preparazione
su un certo argomento, decide di far circolare un foglio con 5
domande (a, b, c, d, e test con risposta si/no) rivolte ai 163
studenti in aula. Il professore un po’ sfiduciato ipotizza che gli
studenti risponderanno a caso, cioè pensa che, detta A la v.a. che
assume il valore “1” quando la risposta alla domanda a è corretta
e “0” altrimenti, la probabilità di non sbagliare sia ϑ=0,5 e lo
stesso per le v.a. B, C, D, E. Ritiene inoltre indipendenti fra loro le
v.a. di cui sopra.
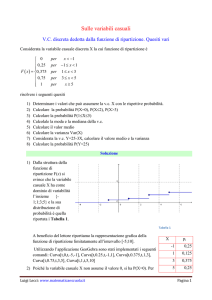
Scrivere la funzione di distribuzione cumulativa e la legge di
probabilità della v.a. A, disegnando il grafico della FA(x).
Il punteggio Xi che ottiene l’i-mo studente come è legato alle v.a.
Ai, Bi, Ci, Di, Ei?
Sempre se l’ipotesi del professore fosse vera , quale distribuzione
dovrebbe avere la Xi?
Indicare la media e la varianza di questa distribuzione, sia come in
questo caso con ϑ=0,5 sia con ϑ qualsiasi.
Se la domanda Ei è più facile delle altre e gli studenti non
rispondono a caso sia ϑ=0,7 (sempre con ϑ=0,5 per le altre
domande). In ipotesi di indipendenza per le v.a. A,B,C,D, E, dopo
aver particolarizzato la distribuzione della v.a Yi che conta le
risposte giuste alle prime quattro domande, date dall’i-mo
studente, calcolare la legge della v.a. Xi.
Calcolare E(X) e var(X) in questo caso.
Come si distribuisce esattamente la v.a. W = X1+X2+…+X163 nel
caso in cui ϑ=0,5 per tutte le domande.
Come si distribuisce approssimativamente la v.a. . W =
X1+X2+…+X163 caso in cui ϑ=0,5 per le prime quattro domande e
ϑ=0,7 per l’ultima?
Con questa approssimazione calcolare P(W=439)
Come si distribuisce (approssimativamente la v.a. W =
X1+X2+…+X163/163 nel caso in cui ϑ è uguale per tutte le
domande.
Il docente vuole distribuire il punteggio dato alla X
proporzionalmente fra 5 e 30. Qual è il legame fra il punteggio R
così trasformato e X. Qual’ la distribuzione di Q =
R1+R2+…+R163/163?
Raccolti i fogli con le risposte si procede alla rilevazione del c.c X1,
… , Xn. Viene di seguito sintetizzato il c.c riportando la frequenza
assoluta delle risposte corrette:
risposte
corrette
studenti
0
1
2
3
4
5
4
11
17
49
57
25
60
50
40
30
20
10
0
0
1
2
3
4
5
Stimare E(X) dimostrando le proprietà dello stimatore utilizzato.
Ricordando il legame fra E(X) e var(X) stimare var(X) dimostrando
le proprietà dello stimatore.
Calcolare un intervallo di confidenza asintotico per E(X) di livello
γ=0,9.
Visto il grafico della frequenza assoluta degli errori sareste
disposti ad accettare l’ipotesi del professore secondo la quale gli
studenti rispondono a caso?
CALCOLO DELLE PROBABILITA’ E STATISTICA MATEMATICA A
30-06-2008
Le figure seguenti mostrano due istogrammi. La prima mostra la
produzione mensile per 255 pozzi di gas naturale (espressa in
103m3). La seconda mostra l’istogramma del logaritmo della
produzione.
L’impressione visiva è che, qualitativamente, la seconda sia
assimilabile ad un andamento normale. Scrivere l’espressione
della densità normale di media  e di varianza 2. Evidenziando
sul grafico il riscontro dei valori  e .
Sia Z una v.a. continua. Calcolare la funzione di distribuzione
cumulativa della v.a. W=aZ+b.
Scrivere la funzione di distribuzione cumulativa della suddetta
normale, esprimendola in funzione di (x).
I (255) dati relativi alla seconda figura sono i
seguenti:1.533787947 1.164244333 … 0.999388823 0.7469922
1.783059591 … 0.829546147.
Per comodità vengono riportati i valori di alcune statistiche
relative ai dati precedenti: somma 411.5326424, somma dei
quadrati 928.1118391; mediana 1.614214414, range
6.289030375.
Supponendo che i dati seguenti siano la realizzazione di un c.c. X1,
X2, … Xn.
Proporre uno stimatore per  ed uno per 2 indicandone le
proprietà incluse le distribuzioni.
Dimostrarne le proprietà.
Il valore della mediana è sensato, confrontato con un opportuno
valore funzione della somma?
Il valore del range è sensato, confrontato con un opportuno
valore funzione della somma e della somma dei quadrati?
Il legame dei dati appena trattati e quelli originali della
produzione è Y=eX. Calcolare la densità della variabile Y,
verificando che si distribuisce come
f Y ( x) 
1
x 2
exp( 
1
2
2
(ln x   ) 2 )
E (Y )  e

2
2
,  Y2  e 2   2  e 2   . Mediante la formula della media
2
2
approssimata e della varianza approssimata, valutare E(eX) e
var(eX).
Sostituire i valori stimati di  e di  nelle valutazioni precedenti.
Stimare E(Y) e var(Y) sulla base del c.c. Y1, Y2, …, Yn, la cui
realizzazione (relativa al primo istogramma) è la seguente:
4.635703404 3.203501187 … 23.01981367 2.292278146.
Anche qui per comodità vengono riportati i valori di alcune
statistiche relative ai dati precedenti: somma 2071.941, somma
dei quadrati 39581.53989.
Calcolare un intervallo di confidenza di livello =0,95 per E(Y).