forze, lavoro, energia – esercizio n. 10
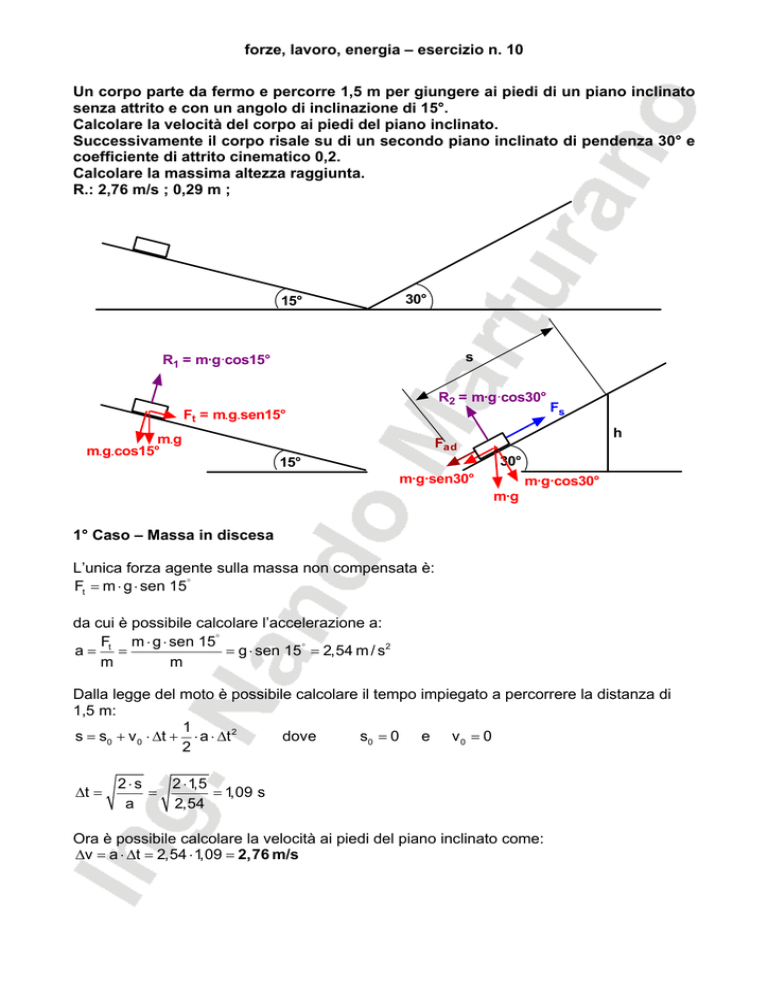
Un corpo parte da fermo e percorre 1,5 m per giungere ai piedi di un piano inclinato
senza attrito e con un angolo di inclinazione di 15°.
Calcolare la velocità del corpo ai piedi del piano inclinato.
Successivamente il corpo risale su di un secondo piano inclinato di pendenza 30° e
coefficiente di attrito cinematico 0,2.
Calcolare la massima altezza raggiunta.
R.: 2,76 m/s ; 0,29 m ;
15°
30°
s
R1 = m·g·cos15°
R2 = m·g·cos30°
Ft = m·g·sen15°
m·g
m·g·cos15°
Fs
h
Fad
30°
15°
m·g·sen30°
m·g·cos30°
m·g
1° Caso – Massa in discesa
L’unica forza agente sulla massa non compensata è:
Ft = m ⋅ g ⋅ sen 15°
da cui è possibile calcolare l’accelerazione a:
F m ⋅ g ⋅ sen 15°
a= t =
= g ⋅ sen 15° = 2,54 m / s2
m
m
Dalla legge del moto è possibile calcolare il tempo impiegato a percorrere la distanza di
1,5 m:
1
s = s0 + v 0 ⋅ ∆t + ⋅ a ⋅ ∆t 2
dove
s0 = 0 e v 0 = 0
2
∆t =
2⋅s
=
a
2 ⋅ 1,5
= 1,09 s
2,54
Ora è possibile calcolare la velocità ai piedi del piano inclinato come:
∆v = a ⋅ ∆t = 2,54 ⋅ 1,09 = 2,76 m/s
forze, lavoro, energia – esercizio n. 10
2° Caso – Massa in salita
Il corpo giunto al fondo del piano inclinato, possiederà una certa energia cinetica e
pertanto sarà in grado di compiere il lavoro necessario per risalire sul secondo piano
inclinato. Dall’eguaglianza tra energia cinetica e lavoro, inteso come prodotto della forza
risultante FR (ricavata dalla rappresentazione dei diagrammi di corpo libero) e lo
spostamento, è possibile ricavare quest’ultimo.
1
Ecin = ⋅ m ⋅ v 2
2
L = FR ⋅ s
Fad = µ d ⋅ R2 = µ d ⋅ m ⋅ g ⋅ cos 30°
(
FR = Fad + m ⋅ g ⋅ sen 30° = µ d ⋅ m ⋅ g ⋅ cos 30° + m ⋅ g ⋅ sen 30° = m ⋅ g ⋅ µ d ⋅ cos 30° + sen 30°
1
⋅ m ⋅ v 2 = FR ⋅ s
2
1
1
1 2
⋅ m ⋅ v2
⋅ m ⋅ v2
⋅v
2
2
s= 2
=
=
=
FR
m ⋅ g ⋅ µ d ⋅ cos 30° + sen 30°
g ⋅ µd ⋅ cos 30° + sen 30°
Ecin = L
⇒
(
)
(
0,5 ⋅ 2,762
=
= 0,576 m
9,81⋅ ( 0,2 ⋅ 0,87 + 0,5 )
Infine è possibile calcolare l’altezza massima a cui giunge il corpo:
h = s ⋅ cos 60° = 0,576 ⋅ 0,5 = 0,29 m
)
)












