Preparazione ai test delle facoltà
scientifiche
Matematica e fisica
Insiemi, numeri e operazioni
1. Dividere un numero per 0,05 è lo stesso che
moltiplicarlo per :
A. 2
B. 5
C. 20
D.50
E.100
2. Dato il prodotto N=2010∙2011∙2012
determinare quale dei seguenti interi non è
divisore di N.
A. 12 B. 15 C. 18 D. 20
E.4022
3. L’espressione (3∙104)∙(3∙10-4) è uguale a:
A. 310-6 B. 3∙108 C. 6∙208 D.32 E.6
4. Quanto vale la decima parte di 1020?
A. 120 B. 102 C.1010
D. 1019
E. 1020
5. Quanto vale l’espressione 103-102?
A. 10
B. 9∙102 C. 9∙10 D.105 E. nessuna
6. L’espressione(2n+2n+1)2 con n intero positivo, è
anche uguale a :
A. 9∙4n
B. 24n+2
C. 44n+2
D.22n +2n
E.34n
2
7. La somma (am+an) equivale.
A. a(m-n)
B. a(m+n)
C. a(m+n)(a-m+a-n)
D. amn
E. am/n
8. (-2)-3 è uguale a :
A. 8
B.6
C.-0,125
D.0,125
E.-4
9. In un esame il punteggio finale può essere un
qualunque numero intero compreso tra 0 e 180
(estremi compresi). Per essere promossi bisogna
ottenere almeno il 45% del punteggio massimo
ammissibile. Qual è il punteggio massimo che èpuò
aver avuto un alunno bocciato?
A. 40
B.90
C.80
D.100
E.70
10. Un infermiere deve somministrare un
farmaco, in quantità diverse a due pazienti:
Mauro e Lucia. Presi 60mg del farmaco,
l’infermiere ne tiene un quarto da parte e divide
il resto tra Mauro e Lucia nel rapporto di 2 a 1.
Quanti milligrammi di farmaco saranno
somministrati a Mauro?
A. 45
B.15 C. 30
D. 40
E. 10
Algebra classica: monomi e polinomi
1. Qual è il risultato dell’espressione
A.
2. Il
− + 6 B.
C.
D.3
E. nessuna
quadrato del trinomio (a-b-c) è uguale a:
3. L’espressione a3-b3 è uguale a:
4. La scomposizione in fattori del polinomio x4-7x3+18x2-20x+8
è:
5. il polinomio 36-a2-2ab-b2 scomposto in fattori
dà:
6. Semplifica l’espressione
()
7. Semplifica l’espressione
Radicali e numeri reali
1. Il radicale è uguale a :
A.
B.
2. L’espressione
A.
B.
C.
D. + + !è uguale a :
C.
D.
3. Qual è il più grande tra i seguenti numeri
A. 67/10 B.62/3 C. 123/5
D. 502/5
E.
E.501/3
4. Eseguire la razionalizzazione di
A.
B.
C.
( )
D. − 5
E.
Equazioni e sistemi di equazioni
1.
Un bambino possiede N biglie. Se ne avesse il triplo ne avrebbe 6
in meno della sorella che ne ha 18. quanto vale N?
A. 4
B.6
C.8
D.12 C.24
2.
Il 5% del 10% di un numero N vale 100. quanto vale N?
A. 1000
B.5000 C.10000
D.20000
E.100000
3.
Se un terzo di un numero è uguale a tre più un quarto del numero
stesso, qual è il numero?
A. 3
B.9
C.12 D.24 E.36
X e y sono due numeri tali che la loro somma dà un numero a e x è
il successivo di y. Quanto vale x2-y2?
A. nn si sa B. a
C. –a D. 2a+1
E. a2
Risolvere la disequazione (2x+x2+1)/(x2-1)>0
A. X>0
B. X<-1 e X>1 C. -1<x<1
D. x<0 E. per ogni x
4.
5.
Logaritmi ed esponenziali
1. Il valore dell’espressione log 0,001 con a ≥0:
A. è un numero sempre positivo
B. è un numero sempre negativo
C. è un numero irrazionale
D. -3/2 per ogni valore di a
E. -3/2 se il valore della base è 10
2. E’ data l’equazione
reali è:
A. 2
B. 4
C.
2x
2
=16. L’insieme di tutte le sue soluzioni
log 8
D. -2; +2
E. − log 16;! log 16
Geometria analitica
1.
Le due rette y=3x+2 e y=18x-4 :
A. si incontrano (0;4) B. si incontrano in (3;1) C. Si incontrano in (0;3) D.
sono parallele E. Sono sghembe
2.
Se y=4x(x+1), il grafico di y in funzione di x in un piano cartesiano è:
A. un cerchio; B. una retta; C. un’iperbole; D. Una parabola; E. un
esponenziale
3.
In un piano cartesiano la distanza tra i punti (2;1) e (3;2) è:
A. 2
B. C. 4
D. 8
E. 8
4.
La circonferenza x2+y2-2x=0 ha il centro:
A. sull’asse x B. sull’asse y C. sulla retta y=x
D. (0;2) E. (0;0)
La regione limitata di piano avente per contorno l’asse delle x, la retta y=2x1 e le rette x=1 e x=3, ha area uguale a :
A. 1
B. 3
C. 4
D. 5
E. 6
5.
Funzioni
+ f(x+1)=
e
1. Data la funzione f(x) tale che
f(1)=2; quanto
vale f(2)?
A. 3
B. O C.1/2
D.2
E.1
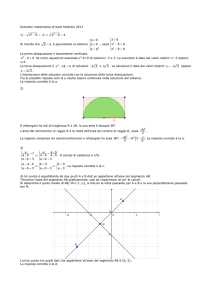
2. La relazione rappresentata nel seguente diagramma:
A. nn è una f.ne
.
B. è una f.ne iniettiva
.
.
C. è una f.ne biiettiva
.
.
D. nessuna
.
.
E. è una f.ne suriettiva
.
.
.
.
3. Quale delle seguenti equazioni rappresenta una funzione y=f(x) tale che
f(2)=-1 e f(-1)=5?
A. y= x2-3x+1 B. y=-2x2+x+8
C. y= –x2+2x-1 D. y=2x2-x-7
4. Il campo di esistenza della funzione
A. x≠-1B. x>-1 C. x>-1 e x≠1
E. y=3x2-2x
log
D. x<-1 E. R
è:
,
C.- =
,
5. La funzione inversa di f(x)=
,
!
,
A. x=
B. - =
,
,
D. - =
6. Il logaritmo in base 5 di 24 :
A. È compreso tra 1 e 2 B. è compreso tra 2 e 3
D. è compreso tra -1 e 1 E. è uguale a 24/5
,
E. - =
,
C. non esiste
Goniometria
1.
2.
3.
L’angolo di 300° corrisponde a :
A. 2π
B. 3/5π C. 5/3π
D.4/3π
L’equazione senx=-1/2 è soddisfatta per:
A. x=0
B. x=-π/6+2kπ C. –π/3+2kπ
π/6+2kπ
E. π/3+2kπ
E.3/4π
D. x=π/6+2kπ opp x=-
Si indichi la relazione errata:
A. sen(-x)=-senx
B. cos(-x)=cosx C. cos(180°-x)=-cosx
D. sen(180°-x)=-senx
E. tg(-x)=-tgx
4. L’equazione senx-cosx=0 ha come soluzione:
Probabilità e statistica
1.
Una scatola contiene 12 cioccolatini: 4 sono fondenti e 8 al latte. Tre
cioccolatini vengono estratti a caso dalla scatola, uno dopo l’altro. Qual è
la probabilità che i tre cioccolatini estratti siano al latte?
A. 3/12
B. 12/55 C. 7/11
D. 14/5 E.3/5
2.
Tirando contemporaneamente due dadi, quante possibilità vi sono di
ottenere lo stesso numero su entrambi?
A. 1/6
B. 1/12
C. 1/24
D. 1/18
E. 1/9
3.
Si hanno 10 quesiti per ognuno dei quali sono suggerite 4 risposte, delle
quali una sola giusta. Calcolare qual è la probabilità di rispondere
correttamente a tutte e dieci le domande se si risponde a caso.
A. 1/49
B. ¼
C. 1/10
D. 1/14 E. (1/4)10
4. La media aritmetica dei seguenti numeri: -16; -6; 0; +10; +16 è
A. 0
B. 0,4
C. 0,8
D. 1,2
E. 1,6
5. In una serie ordinata di 41 dati la mediana è:
A. La media aritmetica del 19° e 20° dato
B. il 21° dato
C. il 20° dato
D. la media aritmetica del 21° e 20° dato
E. Un dato compreso tra il 20° e il 21°
6. Tredici persone si stringono la mano. Ciascuna stringe la mano a tutte le altre.
Quante sono in totale le strette di mano?
A. 13
B.26
C. 78
D. 156 E. 169
Geometria elementare
1. Sapendo che in un triangolo rettangolo un cateto è la metà dell’altro e che
l’area del triangolo è 64 m2, determinare la lunghezza dell’ipotenusa del
triangolo.
A. 12 m B. 14 m C. 18 m D. 24m
E. 36 m
2. Quale delle seguente terne di numeri potrebbe rappresentare la misura
dei lati di un triangolo rettangolo?
A. 7,6,15
B. 3,4,5
C.4,8,12
D. 2,12,5
E. 3, 15,10
3. Due sfere hanno il raggio uno il triplo dell’altro. Quante volte è maggiore il
volume della sfera di raggio maggiore rispetto all’altro?
A. 3
B. π
C. 9
D. 3π E.27
4. La somma degli angoli interni di un esagono nn regolare è:
A. 600° B. 360° C. 720° D. dipende dalla misura dei lati
E. dipende dalla
forma del poligono
Alcuni ex risolti
1. Il rapporto tra i volumi di due cubi è 4. Qual è il
rapporto tra le loro superfici?
A. 2
B.4 C. 4 1/3
D. 4 2/3
E.2 2/3
Sol.ne: il volume del cubo è l3, quindi indicando con l1 ed l2 i lati dei due cubi si ha
/ / =4
ciò che il testo mi chiede è
/ / cioè
/ / . Partendo dalla relaziona nota,
quella dei volumi, vado ad elevare ambo i membri per 2/3 così ottengo
/
/ = 4
quindi semplificando si ha la D
Alcuni es risolti
1. In una successione ereditaria nella quale gli eredi
sono 4 fratelli, al maggiore di essi la defunta madre ha
riservato la quota disponibile e cioè 1/3 dell’eredità.
Supponendo che i 4 fratelli divideranno tra loro in
parti uguali la rimanente quota dei 2/3, quale frazione
dell’eredità spetterà al fratello maggiore?
A. ½
B. 1/3
C. 1/4
D. 1/5
E. 1/6
Indichiamo con x l’intera eredità quindi al fratello maggiore spetterà
+
! quindi facendo i calcoli, la risposta A
2. Il 31 dicembre di ogni anno, l’Istituto di statistica di un
determinato paese pubblica nel proprio rapporto annuale, le
spese mediche sostenute in quell’anno. Ipotizzando una
crescita annua del 30% delle spese mediche, nel Rapporto di
quale anno apparità per la prima volta un ammontare
superiore al doppio della spesa sostenuta nel 2010?
A. 2011
B.2012
C.2013
D.2014
E.2015
Indichiamo con x le spese mediche sostenute nell’anno 2010
Quindi poiché le spese mediche ogni anno aumentano del 30% si ha
2011:
x+0,3x=1,3x
2012:
1,3x+0,3(1,3x)=1,3x+0,39x=1,69x
2013:
1,69x+0,3(1,69x)=1,69x+0,507x=2,197x che è proprio il
doppio di x, quindi la risposta corretta è C
3. Uno studente ha avuto 5 e mezzo ai primi due
compiti. Quale voto dovrà raggiungere al terzo
compito per ottenere la media del 6?
A. 5 e mezzo
,,
=6
B.6
D. 6 e mezzo D. 7 E. Non ce la può fare
risolvendo, si ha D.