La legge di Ampere

La legge di Ampere
Graziano Donati
Legge di Biot e Savart
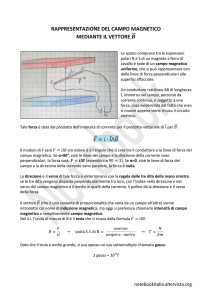
Consideriamo un filo conduttore gerico curvilineo C, infinitamente sottile, percorso dalla corrente stazionaria I.
Consideriamo poi un generico punto dello spazio P(x,y,z) individuato dal vettore generico r=xi+yj+zk. Consideriamo
poi un generico fissato punto P'(x,y,z) del filo conduttore, individuato dal vettore r'=x'i+y'j+z'k. dr' è l'elemento
differenziale della curva C che costituisce il filo conduttore, localizzato nel punto P'(x',x',z'). L'intensità di corrente che
fluisce nel filo conduttore nel punto P'(x',y',z') è indicata con I(x',y',z').
r'(t+dt)
dr' = r'(t+dt)- r'(t)
r'(t)
Mediante una serie di esperimenti è stato possibile ricavare il valore dell'intensità del campo magnetico dH(r) nel
generico punto P(x,y,z), dovuto al solo elemento differenziale di corrente I(x',y',z')dr'=I(r')dr'. La legge di Biot e Savart
(o più correttemente la prima legge elementare di Laplace) afferma che:
dH (r) =
I (rl ) drl sin ^ z h
4r r - rl 2
: AD
m
(Prima Legge Elementare di Laplace in forma scalare)
r=(x,y,z) sono le coordinate generiche in cui è calcolato il campo H
r'=(x',y',z') soo le coordinate generiche dell'elemento differenziale di corrente I(r')dr'
ϕ è l'angolo compreso tra il vettore R=r-r' e l'elemento differenziale di corrente I(r')dr'
L'intensità del campo magnetico H è però una quantità vettoriale e non scalare, quindi è necessario determinare
l'espressione vettoriale di dH, anzichè l'espressione scalare di |dH|. Per la regola del cavatappi, l'intensità del campo
magnetico dH nella figura precedente con il verso della corrente I indicato, deve uscire perpendicolarmente dal piano
del foglio, quindi, la sua direzione e verso sono individuate da un versore n perpendicolare al piano del foglio e uscente
da questo. Tale versore, cioè, deve essere perpendicolare al piano che contiene i vettori R e dr' e deve uscire dal foglio.
Di conseguenza, un tale versore n può essere ottenuto come:
l#
n = dr R
drl # R
quindi:
dH (r) = dH (r)n =
I (rl ) drl sin ^ z h drl # R
4r r - rl 2
drl # R
Poichè |𝑑𝒓′ × 𝑹| = |𝑑𝒓′||𝑹|𝑠𝑖𝑛(𝜙) abbiamo:
dH (r) =
da cui:
dH (r) =
I (rl ) drl sin ^ z h
drl # R
4r r - rl 2
drl R sin ^ z h
I (rl )
drl # R
R
4r r - rl 2
poichè, 𝑹 = 𝒓 − 𝒓′ abbiamo:
dH (r) =
drl # ^ r - rlh
I (rl )
2
l
r - rl
4r r - r
da cui otteniamo:
I (rl ) drl # ^ r - rlh
dH (r) = 4r
r - rl 3
(Prima Legge Elementare di Laplace in forma vettoriale)
A questo punto, per ottenere il campo magnetico totale H(r) nel punto generico P(x,y,z) individuato dal vettore
r=xi+yj+zk, dovuto a tutti i contributi di corrente lungo l'intero filo conduttore, è sufficiente calcolare l'integrale di
linea, lungo la curva C che costituisce il filo conduttore nel quale scorre la corrente I, della precedente espressione.
Abbiamo quindi:
1
H (r) = 4r
# I (rl) drl r#-^rr-l rlh
3
C
e poichè, AxB= - BxA possiamo anche scrivere:
# I (rl) ^rr -- rrllh # drl
1
H (r) =- 4r
: AD
m
3
C
(Legge di Biot e Savart)
e poichè, B=μH risulta anche:
# I (rl) ^rr -- rrllh # drl
n
B (r) =- 4r
6T@ o : W2 D
m
3
C
(Legge di Biot e Savart)
Nel caso di distribuzioni superficiali di corrente JS(r'), abbiamo:
dH (r) =
J S (rl ) dS l # ^ r - rlh
1 J (rl ) # ^ r - rlh dS l
= 4r
S
3
4r
l
r-r
r - rl 3
Nel caso di distribuzioni volumetriche di corrente JV(r'), abbiamo:
dH (r) =
JV (rl ) dV l # ^ r - rlh
1 J (rl ) # ^ r - rlh dV l
= 4r
V
3
4r
r - rl 3
r - rl
Integrando queste due relazioni rispettivamente, sulla superficie S e sul volume V, otteniamo:
1
H (r) = 4r
# J (rl) # ^rr -- rrllh dSl
e
1
H (r) = 4r
# J (rl) # ^rr -- rrllh dV l
e
S
3
S
V
3
V
n
B (r) = 4r
# J (rl) # ^rr -- rrllh dSl
n
B (r) = 4r
# J (rl) # ^rr -- rrllh dV l
S
3
S
V
3
V
Quindi, in definitiva, la legge di Biot e Savart per distribuzioni lineari, superficiali e volumetriche di corrente elettrica
può essere scritta come:
# I (rl) ^rr -- rrllh # drl
^ r - rlh
1
dS l
H (r) = 4r # J (rl ) #
r - rl
^ r - rlh
1
dV l
H (r) = 4r # J (rl ) #
r - rl
1
H (r) =- 4r
3
e
S
S
3
e
S
V
V
3
e
# I (rl) ^rr -- rrllh # drl
n
B (r) =- 4r
3
S
# J (rl) # ^rr -- rrllh dSl
^ r - rlh
n
dV l
B (r) = 4r # J (rl ) #
r - rl
n
B (r) = 4r
S
3
V
3
S
V
Queste relazioni, possono essere considerate come gli analoghi magnetici della legge di Coulomb per i fenomeni
elettrici.
Legge di Ampere
Consideriamo una distribuzione volumetrica di corrente elettrica JV(r') nello spazio, e consideriamo un generico punto
P(x,y,z) individuato dal vettore r=xi+yj+zk. Il vettore densità di flusso magnetico B(r) in tale punto può essere ottenuto
mediante la legge di Biot e Savart che abbiamo appena dimostrato:
n
B ^ r h = 4r
# J ^rlh # ^rr -- rrllh dV l
V
3
V
Dall'analisi vettoriale sappiamo che:
JV ^ rlh #
^ r - rlh
r - rl 3
1
m # JV ^ rlh
r - rl
= dc
Inoltre, per l'identità vettoriale
d # ^ z ^ r h A ^ r hh = z ^ r h d # A ^ r h - A ^ r h # dz ^ r h
da cui:
dz ^ r h # A ^ r h = d # ^ z ^ r h A ^ r hh - z ^ r h d # A ^ r h
si ha:
JV ^ rlh #
^ r - rlh
r - rl 3
1
1 J ^ rlh - 1
d # JV ^ rlh
m # JV ^ rlh = d # c
m
r - rl
r - rl V
r - rl
= dc
Poichè la densità di corrente JV(r') dipende dalle coordinate x',y',z' mentre l'operatore differenziale ∇ è riferito alle
variabili x,y,z allora risulta ∇ × JV(r')=0. Abbiamo allora:
JV ^ rlh #
^ r - rlh
r - rl 3
= d #c
1 J ^ lh
r m
r - rl V
Sostituendo questa espressione nella legge di Biot e Savart, possiamo scrivere:
n
B ^ r h = 4r
# J ^rlh # ^rr -- rrllh dV l = 4rn # d # c r -1 rl J ^rlh mdV l
V
V
3
V
V
L'integrazione è riferita alle variabili x',y',z' mentre l'operatore differenziale ∇ è riferito alle variabili x,y,z. Di
conseguenza, l'operatore ∇ può essere portato fuori dal segno di integrale:
n
B ^ r h = d # d 4r
# Jr -^rrllh dV ln
V
V
Calcolando il rotore di ambo i membri di questa uguaglianza, otteniamo:
n
d # B ^ r h = d # d # d 4r
# Jr -^rrllh dV ln
V
V
n
Ponendo per semplicità 4r
possiamo scrivere:
# Jr -^rrllh dV l = A^ r h
V
V
d # B^ r h = d # d # A^ r h
Per l'identità vettoriale ∇ × ∇ × 𝐴(𝒓) = ∇(∇ ∙ 𝑨(𝒓)) − ∇2 𝑨(𝒓), possiamo scrivere:
d # B ^ r h = d ^ d $ A ^ r hh - d 2 A ^ r h
Sostituendo ad A(r) la sua espressione, abbiamo:
# Jr -^rrllh dV l
# Jr -^rrllh dV ln - d
2
n
d # B ^ r h = d d 4r
# d $ Jr -^rrllh dV ln - d
2
n
d # B ^ r h = d < 4r
# c r -1 rl d $ J ^rlh + J ^rlh $ d r -1 rl mdV lF - d
n
d # B ^ r h = d < 4r
# J ^rlh $ d r -1 rl dV lF - d
n
d # B ^ r h = d d d $ 4r
V
V
n
4r
V
V
Nella parentesi tonda, portando l'operatore di divergenza all'interno dell'integrale di volume, otteniamo:
V
V
n
4r
# Jr -^rrllh dV l
V
V
Utilizzando l'identità vettoriale ∇ ∙ (𝜙(𝒓)𝑨(𝒓)) = 𝜙(𝒓)∇ ∙ 𝑨(𝒓) + 𝑨(𝒓) ∙ ∇𝜙(𝒓), il primo integrale di volume può
essere riscritto nella seguente forma:
V
V
V
2
n
4r
# Jr -^rrllh dV l
V
V
Poichè la densità di corrente JV(r') dipende dalle coordinate x',y',z' mentre l'operatore differenziale ∇ è riferito alle
variabili x,y,z allora risulta ∇ ∙ JV(r')=0. Abbiamo allora:
V
V
2
n
4r
# Jr -^rrllh dV l
V
V
1
1
Poichè risulta ∇ |𝒓−𝒓′| = −∇′ |𝒓−𝒓′| possiamo anche scrivere:
n
d # B ^ r h = d <- 4r
# J ^rlh $ dl r -1 rl dV lF - d
n
d # B ^ r h = d <- 4r
# cdl $
n
d # B ^ r h = d <- 4r
# dl $ Jr -^rrllh dV lF - d
n
d # B ^ r h = d <- 4r
# Jr -^rrllh $ dSlF - d
V
2
V
n
4r
# Jr -^rrllh dV l
V
V
Utilizzando l'identità vettoriale ∇ ∙ (𝜙(𝒓)𝑨(𝒓)) = 𝜙(𝒓)∇ ∙ 𝑨(𝒓) + 𝑨(𝒓) ∙ ∇𝜙(𝒓), da cui:
∇𝜙(𝒓) = ∇ ∙ (𝜙(𝒓)𝑨(𝒓)) − 𝜙(𝒓)∇ ∙ 𝑨(𝒓) otteniamo anche:
1 J ^ lh - 1 dl $ J ^ lh dV l - d 2 n
r
F
V r m
4r
r - rl
r - rl V
V
# Jr -^rrllh dV l
V
𝑨(𝒓) ∙
V
Per l'equazione di continuità della corrente elettrica deve essere ∇′ ∙ JV(r') = 0 quindi otteniamo:
V
2
V
n
4r
# Jr -^rrllh dV l
V
V
Al primo integrale dentro parentesi quadra applichiamo il teorema della divergenza, ottenendo:
V
2
S
n
4r
# Jr -^rrllh dV l
V
V
S è una superficie che racchiude il volume V che contiene tutta la distribuzione di corrente, quindi, il flusso di corrente
attraverso tale superficie deve essere uguale a zero, ciò vuo dire che tale integrale si superficie chiuso risulta essere
nullo. Quindi:
n
d # B ^ r h = d 60@ - d 2 4r
ovvero:
n
d # B ^ r h =-d 2 4r
# Jr -^rrllh dV l
V
V
# Jr -^rrllh dV l
V
V
L'operatore differenziale ∇2 è riferito alle sole variabili x,y,z e quindi può essere portato all'interno del simbolo di
integrale (che è riferito alle variabili x',y',z'), ottenendo:
n
d # B ^ r h =- 4r
# J ^rlh d c r -1 rl mdV l
2
V
V
Sapendo che il laplaciano scalare della funzione 1/|r-r'| è uguale ad una funzione delta di Dirac localizzata nel punto r',
ed esattamente:
d2 c
1
m =- 4rd ^ r - rlh
r - rl
la precedente espressione diventa:
n
d # B ^ r h =- 4r
# J ^rlh^-4rd^r - rlhh dV l
V
V
ovvero:
n
d # B ^ r h = 4r 4r
da cui:
d # B^ r h = n
# J ^rlh d^r - rlh dV l
V
V
# J ^rlh d^r - rlh dV l
V
V
Dalla teoria della funzione delta di Dirac, risulta ∫𝑉 𝑱(𝒓′) 𝛿(𝒓 − 𝒓′)𝑑𝑉 ′ = 𝑱(𝑟) e quindi:
d # B ^ r h = nJV ^ r h
Poichè B(r)=μH(r) possiamo anche scrivere:
d # nH ^ r h = nJV ^ r h
Dividendo ambo i membri per μ abbiamo:
d # H ^ r h = JV ^ r h
Abbiamo quindi il seguente teorema:
TEOREMA. (Legge di Ampere in forma differenziale). Data una distribuzione volumetrica di corrente elettrica
JV(r), essa genererà nello spazio circostante un campo magnetico B(r). Allora, in ogni punto dello spazio, il rotore del
vettore densità di flusso magnetico B(r) è uguale al prodotto del vettore densità di corrente elettrica J(r) per la
permeabilità magnetica del mezzo μ. Ovvero:
d # B ^ r h = nJV ^ r h
d # H ^ r h = JV ^ r h
Calcolando l'integrale di superficie di ambi i membri di questa relazione, su una determinata superficie aperta S,
otteniamo:
# 6d # B (r)@ $ dS = n # J (r) $ dS
V
S
S
Se all'integrale a primo membro applichaiamo il teorema di Stokes, otteniamo:
# B (r) $ dr = n # J (r) $ dS
V
C
S
dove C è la curva che orla la superficie S. Abbiamo quindi il seguente teorema:
TEOREMA. (Legge di Ampere in forma integrale). Data una distribuzione volumetrica di corrente elettrica JV(r),
essa genererà nello spazio circostante un campo magnetico B(r). Allora, l'integrale di linea del vettore densità di flusso
magnetico B(r) calcolato su una qualsiasi curva chiusa C, è uguale alla corrente elettrica totale che attraversa una
generica superficie S orlata dalla curva chiusa C, moltiplicata per la permeabilità magnetica del mezzo μ. Ovvero:
# B (r) $ dr = n # J (r) $ dS
V
C
S
# H (r) $ dr = # J (r) $ dS
V
C
S
La legge di Ampere, verrà successivamente completata da James Clerk Maxwell, con l'aggiunta di un ulteriore termine
detto corrente di spostamento, e formerà così la quarta equazione di Maxwell (o quarta equazione di Ampere Maxwell), che assieme alle altre tre equazioni (legge di Gauss per i campi elettrici, legge di Gauss per i campi
magnetici, legge dell'induzione elettromagnetica di Faraday_Lenz - Neumann), alle due equazioni di continuità per le
correnti elettriche e per le correnti magnetiche, alle tre equazioni costitutive della materia, e alla legge della forza di
Lorentz-Coulomb, andrà a formare la base della teoria elettromagnetica generale.