Integrale definito
Gli integrali sono divisi in due categorie:
1. INTEGRALE INDEFINITO, l’integrale indefinito di una generica funzione f è l’insieme
delle primitive1 di questa funzione. Esso si indica con il simbolo: ∫ f ( x )dx
2. INTEGRALE DEFINITO, prendendo in esame una generica funzione f(x) positiva
dell’intervallo (a,b), l’integrale definito di f(x) nell’intervallo (a,b) è l’area delimitata dalle
funzioni y=f(x); y=0; e dalle rette x=a; x=b. Esso si indica con il simbolo:
∫ f (x )dx
b
a
Nel primo punto il calcolo dell’integrale di una funzione corrisponde all’operatore inverso alla
derivata. Nel secondo punto il calcolo dell’integrale di una funzione porta a determinare una
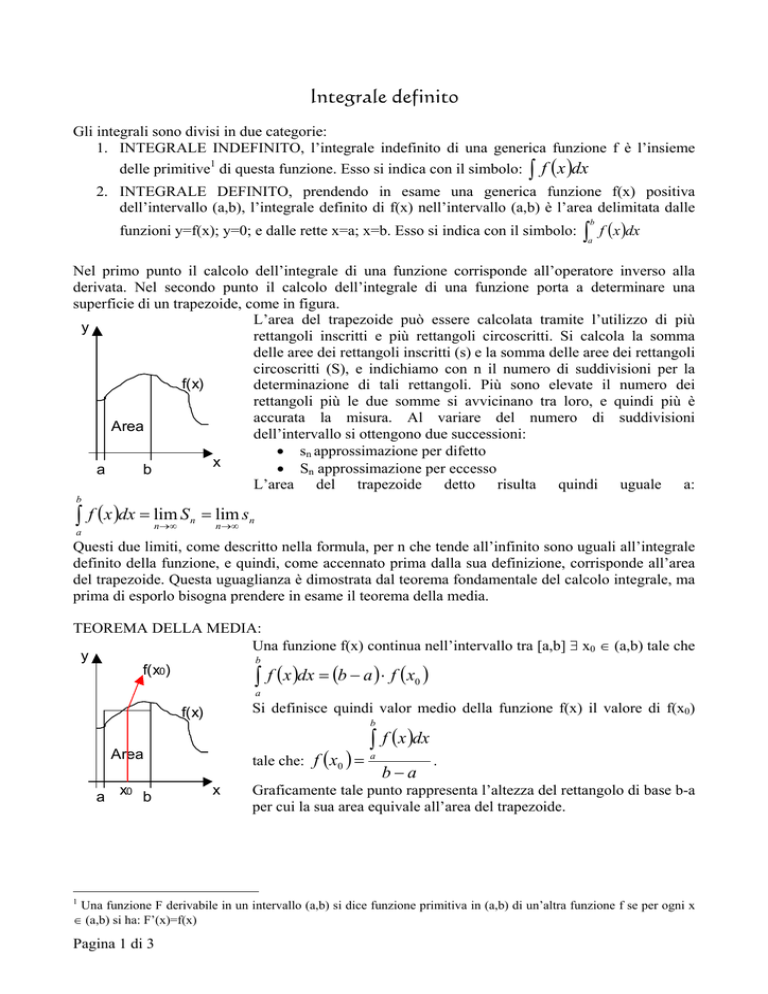
superficie di un trapezoide, come in figura.
L’area del trapezoide può essere calcolata tramite l’utilizzo di più
y
rettangoli inscritti e più rettangoli circoscritti. Si calcola la somma
delle aree dei rettangoli inscritti (s) e la somma delle aree dei rettangoli
circoscritti (S), e indichiamo con n il numero di suddivisioni per la
f(x)
determinazione di tali rettangoli. Più sono elevate il numero dei
rettangoli più le due somme si avvicinano tra loro, e quindi più è
accurata la misura. Al variare del numero di suddivisioni
Area
dell’intervallo si ottengono due successioni:
• sn approssimazione per difetto
x
• Sn approssimazione per eccesso
a
b
L’area del trapezoide detto risulta quindi uguale a:
b
S n = lim sn
∫ f (x )dx = lim
n →∞
n→∞
a
Questi due limiti, come descritto nella formula, per n che tende all’infinito sono uguali all’integrale
definito della funzione, e quindi, come accennato prima dalla sua definizione, corrisponde all’area
del trapezoide. Questa uguaglianza è dimostrata dal teorema fondamentale del calcolo integrale, ma
prima di esporlo bisogna prendere in esame il teorema della media.
TEOREMA DELLA MEDIA:
Una funzione f(x) continua nell’intervallo tra [a,b] ∃ x0 ∈ (a,b) tale che
y
b
f(x0)
f ( x )dx = (b − a ) ⋅ f ( x )
∫
0
a
Si definisce quindi valor medio della funzione f(x) il valore di f(x0)
f(x)
b
tale che: f ( x0 ) =
Area
a x0 b
1
x
∫ f (x )dx
a
b−a
.
Graficamente tale punto rappresenta l’altezza del rettangolo di base b-a
per cui la sua area equivale all’area del trapezoide.
Una funzione F derivabile in un intervallo (a,b) si dice funzione primitiva in (a,b) di un’altra funzione f se per ogni x
∈ (a,b) si ha: F’(x)=f(x)
Pagina 1 di 3
TEOREMA FONDAMENTALE DEL CALCOLO
INTEGRALE
Per poter esporre il teorema fondamentale del calcolo integrale occorre definire la funzione
integrale: H ( x ) = ∫ f (t )dt , si chiama funzione perché l’area varia al variare (in funzione) di x.
x
a
TEOREMA:
Allora, se H(x) è una funzione integrale di f(x) allora H(x) è una primitiva di f(x) cioè H’(x)=f(x).
DIMOSTRAZIONE:
Prendendo in esame la figura si può esprimere l’incremento
della funzione integrale H(x) dalla formula:
H (x + h ) − H (x ) = ∫
x+h
a
f (t )dt − ∫ f (t )dt .
x
a
Con le proprietà dell’integrale definito2, precisamente la 3, è
possibile semplificare l’espressione come segue:
x
x+h
x
x+h
H ( x + h ) − H ( x ) = ∫ f (t )dt + ∫ f (t )dt − ∫ f (t )dt = ∫ f (t )dt .
a
x
a
x
Ora applicando il teorema della media è possibile definire
∫
x+h
f (t )dt = h ⋅ f ( x0 ) , dove h corrisponde alla differenza tra (x+h)-x=h, che nell’enunciato era b-a.
x
Riportandola alla espressione precedente:
H ( x + h ) − H ( x ) = h ⋅ f ( x0 )
H ( x + h ) − H (x ) h ⋅ f (x0 )
=
h
h
H (x + h ) − H (x )
= f (x0 )
h
H (x + h ) − H (x )
Il rapporto
è il rapporto incrementale. Il limite per h che tende a zero di tale
h
H (x + h ) − H (x )
rapporto è: lim
= f ( x ) perché quando h tende a zero x0 tende a x. Il limite di tale
h →0
h
rapporto incrementale è la derivata di H(x) ed essendo tale limite uguale a f(x), allora la derivata di
H(x) è f(x): H’(x)=f(x).
CALCOLO DELL’INTEGRALE DEFINITO MEDIANTE LE PRIMITIVE:
Se H(x) è, quindi, una primitiva di f(x) (come dimostrato) possiamo indicare la generica primitiva
come F ( x ) = H ( x ) + k .
Allora, per la definizione di funzione integrale F ( x ) = ∫ f ( x )dx + k . Nel caso che x sia uguale ad a
x
a
a
la formula diviene F (a ) = ∫ f ( x )dx + k = k . Riportando tale risultato nella formula precedente
a
1.∫ f ( x )dx = − ∫ f ( x )dx
b
a
a
b
2.∫ f ( x )dx = 0
a
a
2
3.∫ f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
b
c
a
a
b
c
4.∫ ( f ( x ) + g (x ))dx = ∫ f ( x )dx + ∫ g ( x )dx
b
b
b
a
a
a
5.∫ k ⋅ f ( x )dx = k ⋅ ∫ f ( x )dx
b
b
a
a
Pagina 2 di 3
x
b
a
a
F ( x ) = ∫ f ( x )dx + F (a ) , e ponendo x uguale a b F (b ) = ∫ f ( x )dx + F (a ) . Per le proprietà di
b
equivalenza delle equazioni, si può riscrivere la formula come
∫ f (x )dx = F (b ) − F (a ) . Essendo
a
l’integrale definito di f(x) l’area di un trapezoide, come detto precedentemente, e F(b) e F(a) le
primitive di tale funzione calcolate in a e b, allora è possibile calcolare l’area di un trapezoide
tramite lo svolgimento di un integrale indefinito per due volte.
Pagina 3 di 3