12/2/2016
L’EQUILIBRIO CHIMICO
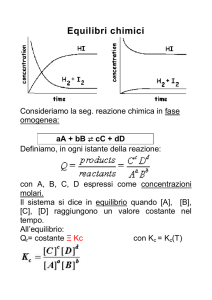
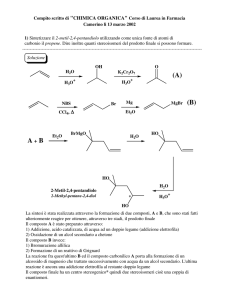
Consideriamo la reazione chimica:
A + B C + D
Quando la velocità della reazione diretta è uguale a quella della
reazione inversa la reazione è all’equilibrio: in questa situazione la
concentrazione di tutti i reagenti e prodotti non varia più nel tempo.
Quando la reazione è all’equilibrio, si trova sperimentalmente che il
rapporto ([C] [D]) / ([A] [B]) è costante: questa costante è chiamata
costante di equilibrio Keq.
[C] [D]
Keq = ————
legge di azione di massa
[A] [B]
(Guldberg e Waage)
Il valore di Keq è caratteristico per ciascuna reazione chimica, e
dipende solo dalla temperatura.
Per a A + b B c C + d D
[C]c [D]d
Keq = ————
[A]a [B]b
1
L’EQUILIBRIO CHIMICO: Kc e Kp
A + B C + D
[C] [D]
Keq = ————
[A] [B]
Maggiore è il valore di Keq , più l’equilibrio è spostato verso la formazione
dei prodotti.
se Keq >>1 [C] [D] >> [A] [B]
se Keq ≈1 [C] [D] ≈ [A] [B]
se Keq <<1 [C] [D] << [A] [B]
aA + b B cC + dD
[C]c [D]d
Keq = Kc = ———— (mol/L)c+d-(a+b)
[A]a [B]b
Per reazioni in fase gassosa:
Pcc PDd
Kp = ———— (atm)c+d-(a+b)
PAa PBb
2
1
12/2/2016
Keq e posizione dell’equilibrio
3
Criteri per l’uso della Keq
1) Nell’espressione della Keq non compaiono mai le concentrazioni di
solidi, liquidi e di solventi in soluzioni diluite.
Esempi:
H2(g) + S(s) H2S(g)
[H2S]
Kc = ———
[H2]
HClO(aq) + H2O H3O+(aq) + ClO-(aq)
ma
CO(g) + H2O(g) CO2(g) + H2(g)
PH2S
Kp = ——
PH2
[H3O+] [ClO-]
Kc = ——————
[ HClO]
[CO2] [H2]
Kc = ———————
[CO] [H2O]
4
2
12/2/2016
Criteri per l’uso della Keq
2) Bilanciamento e costanti di equilibrio. Confrontiamo le equazioni:
S(s) + 3/2 O2(g) SO3(g)
[SO3]
Kc’ = ————
[O2]3/2
2 S(s) + 3 O2(g) 2 SO3(g)
[SO3]2
Kc” = ————
[ O2 ]3
quindi Kc” = (Kc’)2
3) Reazione diretta e inversa
A +B C + D
[C] [D]
Kc(dir) = ————
[A] [B]
C + D A + B
[A] [B]
Kc(inv) = ————
[C[ [D]
quindi K(dir) = 1/K(inv)
5
Criteri per l’uso della Keq
4) Somma di equazioni chimiche:
H2SO3(aq) + H2O H3O+(aq) + HSO3-(aq)
[H3O+][HSO3-]
K1 = ——————
[H2SO3]
HSO3-(aq) + H2O H3O+(aq) + SO3=(aq)
[H3O+][SO3=]
K2 = ——————
[HSO3-]
_______________________________________
H2SO3(aq) + 2 H2O 2 H3O+(aq) + SO3=(aq)
[H3O+]2[SO3=]
Ktot = ——————
[H2SO3]
quindi
Ktot = K1 K2
6
3
12/2/2016
Criteri per l’uso della Keq
5) Relazione tra Kc e Kp:
Pcc PDd
Kp = ————
PAa PBb
aA + bB cC + dD
ma PA = (nA/V) RT = [A] RT
sostituendo:
( [C] RT)c ( [D] RT)d
Kp = —————————
( [A] RT)a ( [B] RT)b
[C]c (RT)c [D]d (RT)d
= ——————————
[A]a (RT)a [B]b (RT)b
Kp = Kc (RT)c+d-(a+b)
e ponendo c+d-(a+b) = Δν
Kp = Kc (RT)Δν
quindi in generale Kp ≠ Kc
ma se Δν=0
Kp = Kc
7
GRADO DI DISSOCIAZIONE
Può essere usato in alternativa alla Keq per reazioni in cui ha luogo una
dissociazione (decomposizione, equilibrio acido/base).
Il grado di dissociazione a è definito come il rapporto tra le moli
dissociate e le moli iniziali.
in.
eq.
AB A + B
n
n-x
x
x
a=x/n
Dalla definizione risulta che 0 ≤ a ≤ 1
In genere si preferisce esprimere il grado di dissociazione come
dissociazione percentuale, quindi se per es. a = 0.15 si dirà che il
composto AB è dissociato per il 15%.
8
4
12/2/2016
EQUILIBRIO MOBILE
PRINCIPIO DI LE CHATELIER
In un sistema all’equilibrio, se si apporta una variazione a uno dei fattori
che determinano l’equilibrio stesso, il sistema si modificherà in modo da
controbilanciare l’effetto di questo cambiamento
Questo è un principio empirico che fornisce un criterio pratico ma non
spiega le ragioni del comportamento previsto, né permette di fare
previsioni quantitative.
In generale, l’effetto della variazione di uno dei parametri che
determinano l’equilibrio può essere previsto con due approcci:
(i) applicando il principio di Le Chatelier
(ii) utilizzando la legge di azione di massa
I due diversi approcci portano alla stessa previsione, ma il secondo
rappresenta il modo più rigoroso di trattare l’equilibrio mobile.
9
Fattori che influenzano l’equilibrio (1)
1) Variazione della concentrazione di un componente del sistema
all’equilibrio:
A + B C + D
il sistema è all’equilibrio: quale sarà l’effetto di un’aggiunta di B?
(i) Previsione in base al principio di Le Chatelier.
Il sistema si comporterà in modo da contrastare la variazione
apportata, quindi si evolverà in modo da consumare almeno in parte
l’eccesso del composto B.
Pertanto l’equilibrio si sposterà verso la formazione dei prodotti.
Quindi
[B]
A + B C + D
10
5
12/2/2016
Fattori che influenzano l’equilibrio (1)
1) segue Variazione della concentrazione di un componente:
A + B C + D
effetto di un’aggiunta di B?
(ii) Previsione in base alla legge di azione di massa.
Per il sistema all’equilibrio si ha che:
[C] [D]
Keq = ————
[A] [B]
Se viene aumentata la [B], ne risulta che
il rapporto delle concentrazioni non sarà più uguale a Keq:
in particolare, tale rapporto sarà inferiore a Keq perché è aumentato il
denominatore.
Il sistema si evolverà in modo da diminuire il denominatore e aumentare il
numeratore, cioè A e B reagiranno per formare C e D.
Si otterranno così nuove concentrazioni dei 4 componenti
[A]’ , [B]’ , [C]’ e [D]’ tali che
[C]’ [D]’
Keq = ————
[A]’ [B]’
Quindi
A + B C + D
[B]
11
Fattori che influenzano l’equilibrio (2)
2) Variazione del volume del reattore sul sistema all’equilibrio:
A(g) + B(g) C(g)
Quale sarà l’effetto di una diminuzione del volume?
(i) Previsione in base al principio di Le Chatelier.
Il sistema si comporterà in modo da contrastare la variazione apportata,
quindi si evolverà in modo da adattarsi meglio al nuovo volume.
L’equilibrio si sposterà verso destra, in modo da diminuire il
numero di particelle totali.
A + B C
Quindi
V
In modo analogo si può discutere l’effetto di una variazione della
pressione totale: infatti dalla P ~ 1/V una diminuzione di volume
corrisponde a un aumento della pressione.
12
6
12/2/2016
Fattori che influenzano l’equilibrio (2)
2) segue Variazione del volume del reattore sul sistema all’equilibrio:
A(g) + B(g) C(g)
effetto di una diminuzione del volume?
(ii) Previsione in base alla legge di azione di massa.
Per il sistema all’equilibrio:
[C]
nC/V
V nC
Kc = ———— = ————— = ————
[A] [B]
nA/V nB/V
nA nB
Se il volume viene diminuito a un nuovo valore V’, il sistema viene
rimosso dall’equilibrio: sarà infatti diminuito il numeratore (V’ nC).
Il sistema si evolverà in modo da far aumentare il numeratore (e
diminuire il denominatore), cioè A e B reagiranno per formare C.
Si otterranno così nuove quantità nA’ nB’ e nC’
tali che:
V’ nC’
Kc = ————
nA’ nB’
Quindi
A + B C
V
13
Fattori che influenzano l’equilibrio (3)
3) Variazione della temperatura del sistema all’equilibrio:
A + B C + Q
reazione esotermica
Quale sarà l’effetto di un aumento della temperatura?
(i) Previsione in base al principio di Le Chatelier.
Il sistema si comporterà in modo da contrastare la variazione apportata:
aumentare la T equivale ad aggiungere calore Q, quindi nel nostro
caso (reazione esotermica) l’equilibrio si sposterà verso sinistra,
in modo da consumare almeno in parte il calore fornito.
Quindi
T
A + B C + Q
reazione esotermica
Nel caso di una reazione endotermica si avrebbe l’effetto opposto:
A + B + Q C
T
14
7
12/2/2016
Fattori che influenzano l’equilibrio (3)
3) segue Variazione della temperatura del sistema all’equilibrio:
A + B C + Q
reazione esotermica
Quale sarà l’effetto di un aumento della temperatura?
(ii) Previsione in base alla legge di azione di massa.
Per il sistema all’equilibrio:
[C]
Keq = ————
[ A] [B]
Non possiamo fare previsioni utilizzando la legge di azione di massa,
perché a una variazione di temperatura corrisponderà anche una
variazione del valore di Keq
15
Fattori che influenzano l’equilibrio (4)
4) Aggiunta di un catalizzatore.
Questa variazione porta a un diverso meccanismo di reazione, e
quindi a un diverso valore di energia di attivazione: pertanto si avrà
una variazione della velocità di reazione.
La posizione dell’equilibrio invece non è influenzata dalla presenza o
meno di un catalizzatore.
Quindi tra la reazione in assenza e quella in presenza di un
catalizzatore cambia la velocità con cui è raggiunto lo stato di
equilibrio, ma non la composizione della miscela di equilibrio.
16
8
12/2/2016
Equilibri in fase gassosa - esempi
1) Prevedere l’effetto di (a) un aumento di pressione e (b) un aumento di
temperatura sul seguente equilibrio:
PCl3 (g) + Cl2 (g) PCl5 (g)
(reazione esotermica)
(a) un aumento di pressione corrisponde a una diminuzione del volume
dalla P ~ 1/V, quindi l’equilibrio si sposterà verso destra, in modo da
diminuire il numero di particelle totali.
P
PCl3 + Cl2 PCl5
T
PCl 3 (g) + Cl2 (g) PCl5 (g) + Q
Quindi
(b)
17
Equilibri in fase gassosa - esempi
2) Prevedere l’effetto di (a) un aumento del volume del reattore e (b) una
diminuzione di temperatura sul seguente equilibrio:
H2 (g) + Cl2 (g) 2 HCl (g)
(reazione endotermica)
(a) il numero di particelle totali dei reagenti è uguale a quello dei prodotti
H2 + Cl2 2 HCl
Quindi
V
=
H2 + Cl2 + Q 2 HCl
(b)
T
18
9
12/2/2016
Equilibri in fase gassosa - esempi
3) Volumi uguali di CO e H2O a 986°C in un reattore di 10.0 L e alla
pressione di 10.0 atm danno la seguente reazione:
CO (g) + H2O (g) CO2 (g) + H2 (g)
A equilibrio raggiunto rimangono 4.86 g di H2O. Trovare Kc e Kp.
CO (g) + H2O (g) CO2 (g) + H2 (g)
in.
n
n
eq. n-x
n-x
x
x
[CO2] [H2]
(x/V) (x/V)
x2
Kc = ————— = —————— = ———
[CO] [H2O]
(n-x)/V (n-x)/V
(n-x)2
ma posso scrivere ntot = 2x + 2(n-x) = 2n da cui n= ntot/2
dalla PV = ntot RT ricavo ntot = 0.967 mol n= ntot/2 = 0.484 mol
Inoltre all’equilibrio n(H2O) = n-x = 4.86 g / 18.02 g mol-1 = 0.270 mol
da cui x = n - 0.270 = 0.484 – 0.270 = 0.214 mol
quindi Kc = x2 / (n-x)2 = (0.214)2 / (0.270)2 =0.628
Kp = Kc (RT)Dn ma Dn = 2 – 2 = 0 e quindi Kp = Kc
19
Equilibri in fase gassosa - esempi
4) 3.0 moli di SO3 vengono introdotte in un recipiente di 5.0 L a 1000 K.
All’equilibrio il 19.7% di SO3 è dissociato in SO2 e O2. Calcolare Kc.
in.
eq.
oppure
SO3 (g) SO2 (g) + ½ O2 (g)
n
n-x
x
x/2
n(1-a)
na
na/2
con a = x/n = 0.197
[SO2] [O2]1/2
Kc = —————
[SO3]
ma [SO3] = n(1-a)/V = 3.0 (1- 0.197)/5.0 = 0.482 mol/L
[SO2] = na/V = (3.0 x 0.197)/5.0 = 0.118 mol/L
[O2] = na/2V = (3.0 x 0.197)/(2 x 5.0) = 0.059 mol/L
quindi
Kc = 0.118 x (0.059)1/2 / 0.482 = 0.0595 (mol/L)1/2
20
10
12/2/2016
Equilibri in fase gassosa - esempi
5) Per la reazione: A(g) + B (g) C (g) si ha l’equilibrio a 400°C
quando, partendo da 1.0 moli di A e 1.0 moli di B, si ottengono 0.20
moli di C. Calcolare come varia la composizione quando si
aggiungono 0.5 moli di C, sapendo che la pressione totale è di 10.0
atm e rimane invariata.
in.
eq.
A + B C
1.0 1.0
0.8 0.8
0.2
ma PC=Pt nC/nt
in.
eq.
Kp = PC/(PA PB)
da cui: Kp= (nC nt)/(nA nB Pt) = 0.056 atm
A + B C
0.8
0.8
0.7
0.8+x 0.8+x
0.7-x
Kp = (nC nt)/(nA nB Pt)= 0.056 1.56 x2 + 2.5x – 1.25 = 0 x = 0.40 mol
nA = nB = 0.8 + 0.4 = 1.2 mol; nC = 0.7 – 0.4 = 0.3 mol
21
11