Modulo di Matematica ed Informatica per il Corso di Laurea

Modulo di Matematica ed Informatica per il Corso di Laurea in Farmacia
Soluzioni dello scritto del 30 giugno 2014
Esercizio 1.
Indichiamo con xi le pressioni diastoliche registrate in millimetri di mercurio (mmHg), in
ordine crescente, e calcoliamo le rispettive frequenze assolute fi :
x1 = 78,
f1 = 3,
x2 = 80,
f2 = 4,
x3 = 82,
f3 = 3,
x4 = 83,
f4 = 3,
x5 = 84,
f5 = 2,
x6 = 85,
f6 = 3,
x7 = 86,
f7 = 4,
x8 = 88,
f8 = 3.
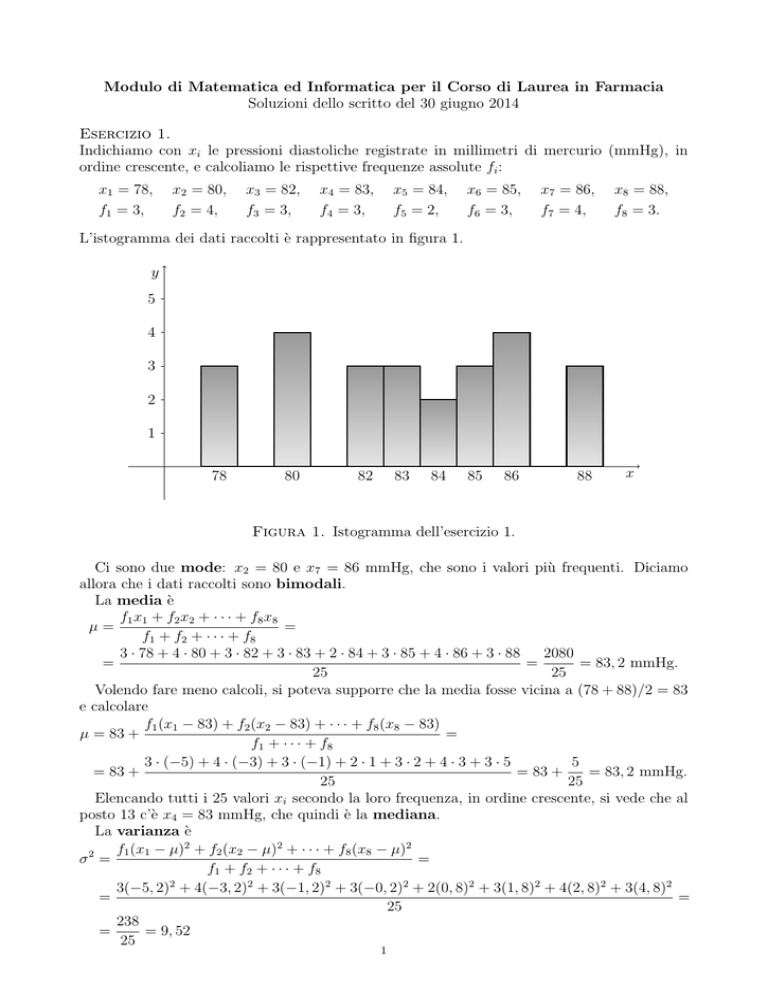
L’istogramma dei dati raccolti è rappresentato in figura 1.
y
5
4
3
2
1
78
80
82
83
84
85
86
88
x
Figura 1. Istogramma dell’esercizio 1.
Ci sono due mode: x2 = 80 e x7 = 86 mmHg, che sono i valori più frequenti. Diciamo
allora che i dati raccolti sono bimodali.
La media è
f 1 x1 + f 2 x2 + · · · + f 8 x8
µ=
=
f1 + f2 + · · · + f8
3 · 78 + 4 · 80 + 3 · 82 + 3 · 83 + 2 · 84 + 3 · 85 + 4 · 86 + 3 · 88
2080
=
=
= 83, 2 mmHg.
25
25
Volendo fare meno calcoli, si poteva supporre che la media fosse vicina a (78 + 88)/2 = 83
e calcolare
f1 (x1 − 83) + f2 (x2 − 83) + · · · + f8 (x8 − 83)
µ = 83 +
=
f1 + · · · + f8
3 · (−5) + 4 · (−3) + 3 · (−1) + 2 · 1 + 3 · 2 + 4 · 3 + 3 · 5
5
= 83 +
= 83 +
= 83, 2 mmHg.
25
25
Elencando tutti i 25 valori xi secondo la loro frequenza, in ordine crescente, si vede che al
posto 13 c’è x4 = 83 mmHg, che quindi è la mediana.
La varianza è
f1 (x1 − µ)2 + f2 (x2 − µ)2 + · · · + f8 (x8 − µ)2
σ2 =
=
f1 + f2 + · · · + f8
3(−5, 2)2 + 4(−3, 2)2 + 3(−1, 2)2 + 3(−0, 2)2 + 2(0, 8)2 + 3(1, 8)2 + 4(2, 8)2 + 3(4, 8)2
=
=
25
238
=
= 9, 52
25
1
√
√
da cui segue che lo scarto quadratico medio è σ = σ 2 = 9, 52 ' 3, 085 mmHg, dove '
significa “circa”.
Riassumendo: la media è 83,2 mmHg, la mediana è 83 mmHg, le mode sono 80 mmHg e
86 mmHg, la varianza è 9,52 e lo scarto quadratico medio è circa 3,085 mmHg.
Esercizio 2.
Indichiamo con
Ω: gli studenti che sono esaminati;
C1 : l’evento che uno studente sia esaminato dalla prima commissione;
C2 : l’evento che uno studente sia esaminato dalla seconda commissione;
C3 : l’evento che uno studente sia esaminato dalla terza commissione;
B: l’evento che uno studente sia bocciato.
quindi Ω \ B è l’evento che uno studente sia promosso.
Il testo dell’esercizio ci dice che
p(C1 ) = p(C2 ) = p(C3 ),
p(B|C1 ) = 20%,
p(B|C2 ) = 35%,
p(B|C3 ) = 65%.
Al punto (a) l’esercizio ci chiede di calcolare la probabilità condizionata p(C2 |B), mentre
al punto (b) ci chiede di calcolare p(C2 |(Ω \ B)).
Siccome C1 ∪ C2 ∪ C3 = Ω e C1 ∩ C2 = ∅ = C1 ∩ C3 = C2 ∩ C3 (si dice che C1 , C2 e C3
formano una partizione di Ω), si ha che
1
p(C1 ) + p(C2 ) + p(C3 ) = 1, quindi p(C1 ) = p(C2 ) = p(C3 ) = .
3
(a) Per la formula di Bayes, combinata con la formula delle probabilità totali, si ha
p(B|C2 ) p(C2 )
p(B|C2 ) p(C2 )
=
=
p(B)
p(B|C1 ) p(C1 ) + p(B|C2 ) p(C2 ) + p(B|C3 ) p(C3 )
35
7
·1
7
100 3
60
= 20 1
' 29, 17%,
35
1
65
1 = 2 =
24
· + 100 · 3 + 100 · 3
100 3
5
p(C2 |B) =
dove ' significa “circa” e abbiamo approssimato la percentuale alla seconda cifra decimale.
(b) Al punto (a) abbiamo calcolato che p(B) = 2/5 = 0, 4 = 40%, quindi p(Ω \ B) =
1 − p(B) = 3/5 = 0, 6 = 60%. Inoltre dal testo segue che
13
p((Ω \ B)|C2 ) = 1 − p(B|C2 ) = 65% = .
20
Possiamo concludere allora applicando ancora la formula di Bayes:
p(C2 |(Ω \ B)) =
p((Ω \ B)|C2 ) p(C2 )
=
p(Ω \ B)
13
20
·
3
5
1
3
=
13
' 36, 11%.
36
In conclusione la risposta alla domanda (a) è 7/24 ' 29, 17%, mentre la risposta alla
domanda (b) è 13/36 ' 36, 11%.
Esercizio 3.
Il logaritmo è definito se il suo argomento è positivo e 2x > 0 se e solo se x > 0, quindi il
dominio della funzione è R>0 =]0, +∞[.
La funzione f non è pari né dispari, perché il dominio non lo consente. Per la stessa ragione,
f non può essere periodica.
Studiamo il segno della funzione f . Essendo un quadrato, log2 (2x) > 0 vale sempre.
Siccome nel dominio vale x > 0, si ha che f è sempre negativa o nulla.
Vediamo le intersezioni del grafico di f con gli assi cartesiani. Siccome x = 0 è fuori dal
dominio, la funzione f non interseca l’asse y. Posto f (x) = 0, si ha
−x log2 (2x) = 0
2
se x = 0, che non è accettabile perché fuori dal dominio, oppure se log(2x) = 0, cioè se
2x = e0 = 1, che vale se e solo se x = 1/2. Quindi il grafico di f interseca l’asse x nel punto
(1/2, 0).
Studiamo gli eventuali asintoti della funzione f (x). Si ha
lim+ −x log2 (2x) = 0 · (−∞)2 = 0 · ∞,
x→0
che è forma indeterminata. Per calcolare il limite, si può procedere cosı̀:
lim+ −x log2 (2x) = lim+ −
x→0
x→0
log2 (2x)
1
x
e applicare i teoremi di De l’Hôpital due volte. Oppure possiamo procedere per sostituzione
nel modo seguente: poniamo x = 1/y, cosı̀ y = 1/x e
log2 (2y)
log2 (2/y)
= lim −
lim −x log (2x) = lim −
y→∞
y→∞
x→0+
y
y
2
che tende a 0 per le gerarchie di infinito. (Abbiamo usato il fatto che log(1/y) = − log(y) e
quindi log2 (1/y) = (− log(y))2 = log2 (y).) Perciò il grafico di f si avvicina all’origine (0, 0)
per x → 0+ e non esistono asintoti verticali.
Riguardo agli altri asintoti, si ha
lim −x log2 (2x) = −∞ · (∞)2 = −∞,
x→+∞
quindi non esistono asintoti orizzontali. Per verificare se ci siano asintoti obliqui calcoliamo
f (x)
= lim − log2 (2x) = −∞,
x→+∞
x
perciò non esistono asintoti obliqui.
Calcoliamo la derivata prima di f . Essendo f un prodotto, si ha
lim
x→+∞
Df (x) = D(−x) log2 (2x) + (−x)D(log2 (2x)) = − log2 (2x) − x2 log(2x)
1
2=
2x
= − log2 (2x) − 2 log(2x) = − log(2x)(log(2x) + 2).
Per studiare il segno di f 0 , osserviamo che log(2x) > 0 se e solo se 2x > 1, cioè se e solo se
x > 1/2. Similmente, si ha log(2x) + 2 > 0 se e solo se
1
1
⇐⇒ x > 2 .
2
e
2e
0
2
Quindi f > 0 se e solo se 1/(2e ) 6 x 6 1/2. Ne segue che f (x) è decrescente per
0 < x < 1/(2e2 ), ha un minimo relativo in x1 = 1/(2e2 ), dove f (x1 ) = f (1/(2e2 )) = −2/e2 ,
è crescente per 1/(2e2 ) < x < 1/2, ha un massimo assoluto in x2 = 1/2 dove f (x2 ) =
f (1/2) = 0, è decrescente per x > 1/2.
La derivata seconda di f è
log(2x) > −2 ⇐⇒ 2x > e−2 =
D(f 0 (x)) = −D(log2 (2x)) − D(2 log(2x)) = −2 log(2x)
= −2
1
1
2−2 2=
2x
2x
1
2
log(2x)
− 2 = − (log(2x) + 1).
x
x
x
Siccome
1
1
⇐⇒ x >
e
2e
00
si ha f > 0 se e solo se 0 < x < 1/(2e). Ne segue che f è convessa per 0 < x < 1/(2e), ha
un flesso in x3 = 1/(2e) dove f (x3 ) = f (1/(2e)) = −1/(2e), è concava per x > 1/(2e).
Si può allora tracciare un grafico approssimativo della funzione f (x) come nella figura 2.
log(2x) + 1 > 0 ⇐⇒ log(2x) > −1 ⇐⇒ 2x > e−1 =
3
y
( 12 , 0)
x
1
1
( 2e
, − 2e
)
( 2e12 , − e22 )
Figura 2. Grafico della funzione f (x) dell’esercizio 3
Esercizio 4.
Siccome log(1) = 0 ed e − e1 = 0, il limite è una forma indeterminata 00 . Applicando i teoremi
di De L’Hôpital, troviamo che
1
log(x)
1
x
lim−
= lim−
= − ' −0, 368.
x
x
x→1 e − e
x→1 −e
e
Esercizio 5.
Sommando e sottraendo ex al numeratore, si ha
Z
Z
Z Z
Z
1
1 − ex + ex
1 − ex
ex
−ex
dx
=
dx
=
+
dx =
dx
=
1
dx
−
1 − ex
1 − ex
1 − ex 1 − ex
1 − ex
= x − log |1 − ex | + c,
dove c è una costante. Considerando gli estremi dell’intervallo di integrazione, si trova allora
Z 2
1
dx = [x − log |1 − ex |]21 = 2 − log 1 − e2 − 1 + log |1 − e| =
x
1 1−e
e−1
1
2
= 1 − log(e − 1) + log(e − 1) = 1 + log 2
= 1 + log
=
e −1
e+1
= 1 − log(e + 1) ' −0, 313.
Dipartimento di Matematica e Informatica — Università degli Studi di Ferrara
4