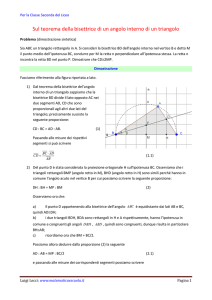
Sia ABC il triangolo dato e D, E ed F i piedi delle altezze su BC, CA e AB rispettivamente.
Essendo <AEB=<ADB=90°, il quadrilatero ABDE e' inscrittibile. Analogamente dal fatto che
<ADC=<AFC=90° segue che AFDC e' inscrittibile.
Se ABC e' acutangolo (fig. 1) si
ha che <ACF=<ABE, in quanto
complementari
dello stesso angolo <BAC.
D'altro canto <ACF=<ADF, in
quanto angoli sulla
circonferenza che sottendono lo
stesso arco e, per la stessa
ragione,
<ABE=<ADE. Da queste
relazioni si ricava che
<ADE=<ADF, cioe' l'altezza AD
e' la bisettrice dell'angolo <FDE.
In modo analogo si puo' procede
per gli angoli in E ed F del
triangolo ortico DEF.
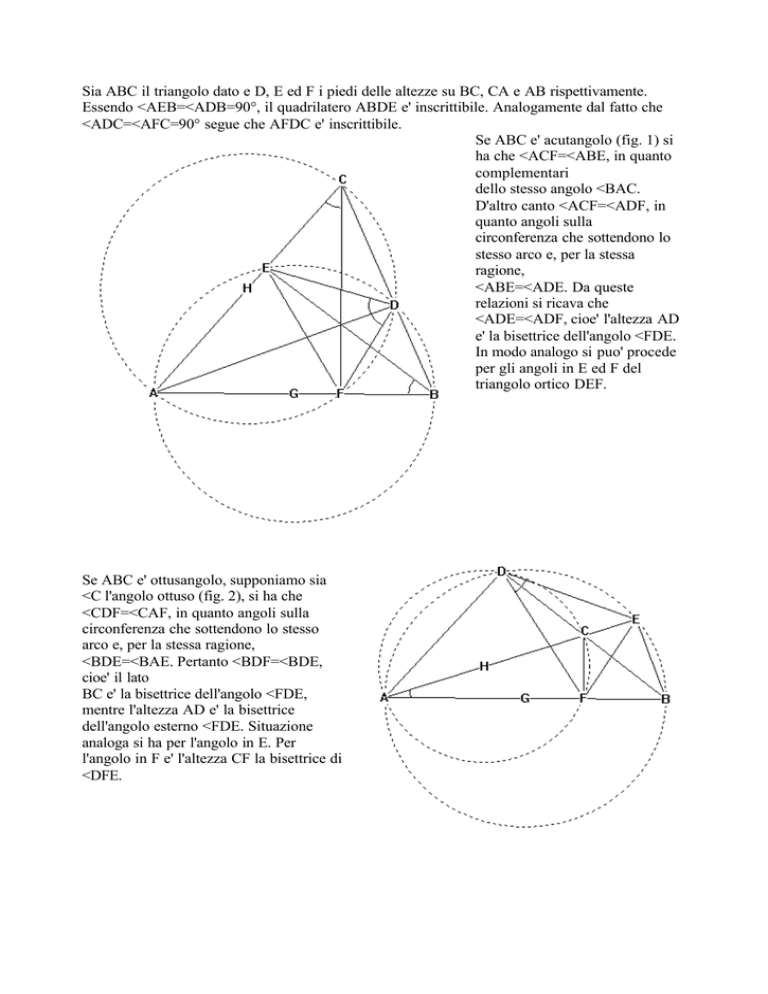
Se ABC e' ottusangolo, supponiamo sia
<C l'angolo ottuso (fig. 2), si ha che
<CDF=<CAF, in quanto angoli sulla
circonferenza che sottendono lo stesso
arco e, per la stessa ragione,
<BDE=<BAE. Pertanto <BDF=<BDE,
cioe' il lato
BC e' la bisettrice dell'angolo <FDE,
mentre l'altezza AD e' la bisettrice
dell'angolo esterno <FDE. Situazione
analoga si ha per l'angolo in E. Per
l'angolo in F e' l'altezza CF la bisettrice di
<DFE.