Sul teorema della bisettrice di un angolo interno di un triangolo

Per la Classe Seconda del Liceo
Sul teorema della bisettrice di un angolo interno di un triangolo
Problema (dimostrazione sintetica)
Sia ABC un triangolo rettangolo in A. Si consideri la bisettrice BD dell’angolo interno nel vertice B e detto M
il punto medio dell’ipotenusa BC, condurre per M la retta n perpendicolare all’ipotenusa stessa. La retta n
incontra la retta BD nel punto P. Dimostrare che CD2MP.
Dimostrazione
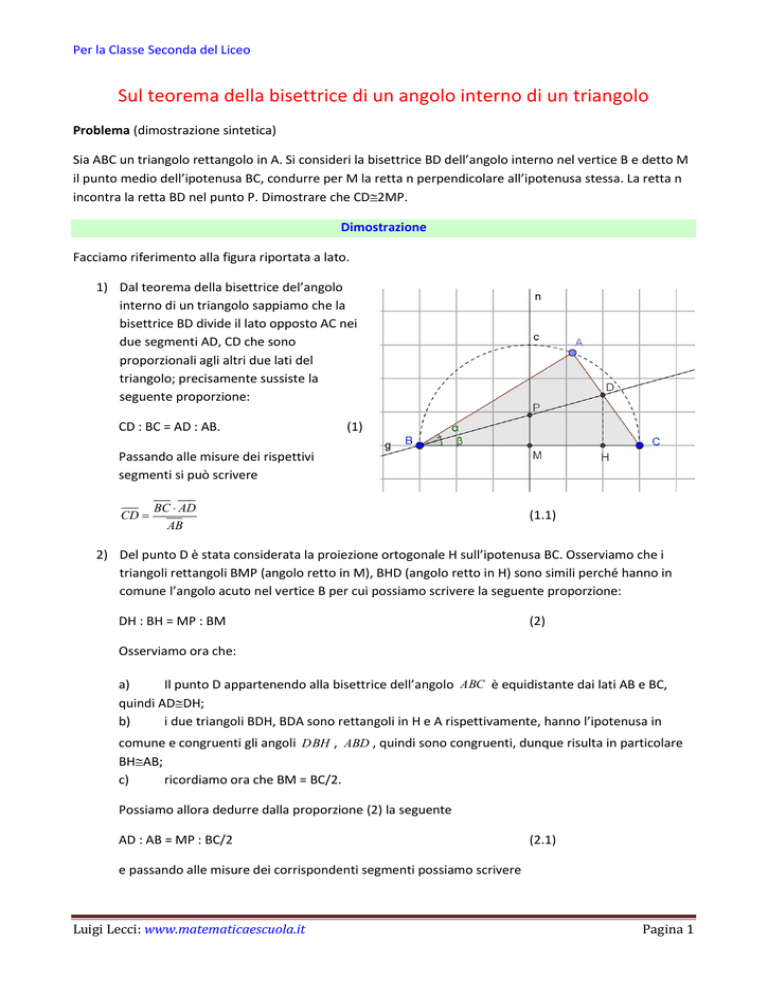
Facciamo riferimento alla figura riportata a lato.
1) Dal teorema della bisettrice del’angolo
interno di un triangolo sappiamo che la
bisettrice BD divide il lato opposto AC nei
due segmenti AD, CD che sono
proporzionali agli altri due lati del
triangolo; precisamente sussiste la
seguente proporzione:
CD : BC = AD : AB.
(1)
Passando alle misure dei rispettivi
segmenti si può scrivere
CD 
BC  AD
AB
(1.1)
2) Del punto D è stata considerata la proiezione ortogonale H sull’ipotenusa BC. Osserviamo che i
triangoli rettangoli BMP (angolo retto in M), BHD (angolo retto in H) sono simili perché hanno in
comune l’angolo acuto nel vertice B per cui possiamo scrivere la seguente proporzione:
DH : BH = MP : BM
(2)
Osserviamo ora che:
a)
Il punto D appartenendo alla bisettrice dell’angolo ABC è equidistante dai lati AB e BC,
quindi ADDH;
b)
i due triangoli BDH, BDA sono rettangoli in H e A rispettivamente, hanno l’ipotenusa in
comune e congruenti gli angoli DBH , ABD , quindi sono congruenti, dunque risulta in particolare
BHAB;
c)
ricordiamo ora che BM = BC/2.
Possiamo allora dedurre dalla proporzione (2) la seguente
AD : AB = MP : BC/2
(2.1)
e passando alle misure dei corrispondenti segmenti possiamo scrivere
Luigi Lecci: www.matematicaescuola.it
Pagina 1
Per la Classe Seconda del Liceo
MP 
AD  BC
, da cui si ricava
2  AB
2MP 
AD  BC
AB
(2.2)
Conclusione
Dal confronto delle relazioni (1.1) , (2.2) si deduce che CD  2MP e quindi la tesi.
Luigi Lecci: www.matematicaescuola.it
Pagina 2