4a Esercitazione: soluzioni
A cura di Monica Bonacina
Corso di Microeconomia A-K, a.a. 2013-2014
Questo eserciziario sostituisce gli esercizi di …ne capitolo del vostro libro di testo.
La struttura degli esercizi è analoga a quella che troverete all’esame.
Ciascun capitolo dell’eserciziario si compone di tre sezioni. Nella prima sezione,
chiamata "De…nizioni", vi si chiede di de…nire sinteticamente alcuni termini. Qualora
fosse necessario potrete avvalervi dll’aiuto di formule o/o gra…ci. Nella seconda
sezione, chiamata "Vero/Falso", vi si chiede di dire se gli enunciati riportati sono
da considerarsi veri, falsi o incerti e di fornire una spiegazione della vostra risposta.
Mi raccomando, concentratevi sulla spiegazione perchè è la parte più importante. La
terza sezione, chiamata "Esercizi", contiene degli esercizi. Gli esercizi possono essere
sia numerici che di analisi gra…ca.
Buon lavoro!!
La maggior parte dei quesiti riportati di seguito è tratta da temi d’esame
Argomenti trattati in questa esercitazione: scelte in condizioni di incertezza, informazione nascosta (selezione avversa) ed azione nascosta (azzardo morale). Prerequisito allo svolgimento dei quesiti contenuti nell’esercitazione
è lo studio del Libro di Testo, Lavanda Italo e Rampa Giorgio, Microeconomia.
Scelte individuali e benessere sociale, Carocci (ed.), 2004, pag. 233-256.
Ragazzi, se avete bisogno di contattarmi, la mia mail è [email protected]!
1
1
A - De…nizioni.
Si de…niscano sinteticamente i termini anche con l’ausilio, qualora necessario, di formule e gra…ci. Per ogni de…nizione corretta viene attribuito 1 punto.
Def. 1. Informazione nascosta.
Soluzioni. Situazione nella quale una parte del mercato non è in condizione di
valutare in maniera completa la qualità dei beni/servizi o¤ erti.
Def. 2. Lotteria.
Soluzioni. Una lotteria è una variabile casuale i cui valori sono somme monetarie.
Def. 3. Utilità attesa di una lotteria.
Soluzioni. L’utilità attesa di una lotteria è il valore atteso dell’utilità di ciascuno
dei possibili risultati di una lotteria, ciascuno pesato per le rispettive probabilità.
Def. 4. Valore atteso di una lotteria.
Soluzioni. Il valore atteso di una lotteria è il valore atteso delle vincite monetarie che la lotteria o¤ re, ciascuna ponderata con la corrispondente probabilità.
Def. 5. Funzione di utilità concava rispetto alla ricchezza.
Soluzioni. Si tratta del caso in cui l’utilità marginale della ricchezza è decrescente. È la tipica funzione di utilità di un soggetto avverso al rischio: infatti un
aumento di ricchezza di X arreca all’individuo una variazione di utilità inferiore alla
riduzione di utilità arrecata da una eguale (X) diminuzione di ricchezza.
Def. 6. Certo equivalente di una lotteria.
Soluzioni. Si consideri una lotteria caratterizzata da valore atteso pari a EV e
da un’utilità attesa pari a EU. Il certo equivalente di questa lotteria per un individuo
è quella somma che, se ricevuta con certezza garantirebbe all’individuo considerato
la stessa utilità della lotteria. Formalmente se le preferenze dell’individuo per la ricchezza sono rappresentate dalla generica funzione di utilità U (x) = xa , possiamo dire
che il certo equivalente è tale per cui U (x) = EU ovvero xa = EU da cui x = EU 1=a .
Def. 7. Assicurazione equa a risarcimento integrale (anche detta assicurazione attuarialmente equa a copertura integrale).
2
Soluzioni. Un’assicurazione è de…nita equa (o attuarialmente equa) se il premio
richiesto dalla compagnia assicurativa è pari al danno atteso per l’assicurato. Tale
assicurazione consente di trasformare una lotteria in una situazione certa caratterizzata da una ricchezza pari al valore atteso della lotteria. Ad esempio. Considerate
un individuo che dispone di una ricchezza monetaria pari a M nel caso in cui non
si veri…chi alcun evento sfavorevole e pari a zero nel caso in cui si veri…chi l’evento
sfavorevole.1 Sapendo che la probabilità che l’evento sfavorevole si veri…chi è pari
a , quanto sopra implica che l’individuo - in assenza di sottoscrizione della polizza
assicurativa - dispone di una ricchezza pari a
M
+ zero
(1
)
| {z }
probabilità di
non subire danni
|{z}
probabilità
di danno
= M (1
);
ne consegue che il danno atteso dall’individuo in assenza di polizza assicurativa è
M M (1
) = M . Un contratto assicurativo equo chiederebbe all’individuo in
questione un premio pari al danno atteso, M , ed in cambio risarcirebbe integralmente
l’individuo nel caso in cui si veri…casse l’evento dannoso. Ne consegue che l’individuo
scegliendo di assicurarsi si garantirebbe una ricchezza pari a
3
2
6
6
6
6
6
6
6M
6
6
6
6
4
(1
)
+
| {z }
probabilità di
non subire danni
(zero + M )
|
{z
}
perdo tutto ma
l’assicurazione mi
rimborsa integralmente
7
7
7
7
7
7
= M (1
M
7
|{z}
|{z}
7
7
premio
probabilità 7
7
di danno 5 assicurativo
Assicurandosi l’individuo si garantisce una ricchezza certa pari al valore atteso della
lotteria.
1 Da notare che nel caso in cui si vei…casse l’evento sfavorevole l’individuo considerato subirebbe
un danno esattamente pari a M in quanto perderebbe tutta la sua ricchezza.
3
)
2
Vero/Falso.
Si stabilisca se gli enunciati sono veri, falsi, o incerti. Si fornisca una spiegazione
(anche gra…ca se opportuno) e si argomenti compiutamente la risposta.
Vero/Falso 8. Se la funzione di utilità di un soggetto è convessa, allora questi sarà
sicuramente avverso al rischio.
Soluzioni. FALSO. Per un individuo avverso al rischio, l’utilità cresce sempre
meno all’aumentare della vincita. La funzione di utilità corrispondente è quindi concava.
Vero/Falso 9. In presenza di informazione nascosta, uno scambio avvantaggia
sempre la parte meglio informata.
Soluzioni. FALSO. Consideriamo il caso di vantaggio informativo dei produttori sui consumatori e supponiamo che malgrado l’asimmetria informativa avvengano
scambi di prodotti sia di alta che di bassa qualità. I produttori di beni di bassa qualità
si avvantaggiano dello scambio a discapito vuoi di quella parte di consumatori (imperfettamente informati) che scoprono di aver acquistato beni di bassa qualità, vuoi
dei produttori di beni di alta qualità (perfettamente informati) che sono costretti ad
accettare un prezzo inferiore alla reale disponibilità a pagare dei consumatori per il
loro prodotto.
Vero/Falso 10. Si consideri una lotteria che promette due vincite monetarie (M) 0
e 10, ciascuna con probabilità 12 . Se un soggetto ha la funzione di utilità U (M ) = M 2
allora l’utilità attesa della lotteria per quel soggetto e 5.
Soluzioni. FALSO. L’utilità attesa (EU) è la media ponderata delle utilità
nei due casi (M=0 e M=10), ciascuna pesata per le probabilità che i due eventi si
veri…chino quindi
EU = 12 U (0) + 12 U (10) = 50
Vero/Falso 11. Un individuo avverso al rischio non acquisterà mai il biglietto di
una lotteria il cui prezzo è pari alla vincita attesa.
Soluzioni. VERO. Entrambi gli eventi garantirebbero un’analoga vincita ma
la partecipazione alla lotteria è più rischiosa (la varianza è maggiore); quindi un
soggetto avverso al rischio preferirà non acquistare il biglietto.
Vero/Falso 12. Si consideri una lotteria che promette le vincite monetarie (M) 0
e 100, ciascuna con probabilità 12 . Se un soggetto ha la funzione di utilità U(M) =
M0:5 allora l’utilità attesa della lotteria per quel soggetto e 50.
Soluzioni. FALSO. L’utilità attesa (EU) è la media ponderata delle utilità nei
due casi (M=0 e M=100) ponderata per le probabilità che i due eventi si veri…chino
4
quindi
EU = 12 U (0) + 12 U (100) = 5
Vero/Falso 13. Marcello trova per strada un biglietto della lotteria. La lotteria
promette una vincita di 10e con probabilità 1/2. Guido o¤re a Marcello 5e in cambio del biglietto della lotteria. Marcello, che è avverso al rischio, ri…uta.
Soluzioni. FALSO. Il valore atteso della lotteria (EV) è la media delle vincite
nei due casi (M=0 e M=10) ponderata per le probabilità che i due eventi si veri…chino
quindi
EV = 12 (0) + 12 (10) = 5
Se Marcello fosse avverso al rischio e gli si o¤ risse la possibilità di scambiare la lotteria cn una somma certa peri al valore atteso della lotteria accetterebbe sicuramente
la somma certa.
Vero/Falso 14. Aldo può acquistare per 12 euro il biglietto di una lotteria che
promette una vincita nulla, di 9 o di 27 euro con la stessa probabilità. Se Aldo fosse
neutrale al rischio sicuramente sceglierebbe di non acquistare il biglietto.
Soluzioni. FALSO. Il valore atteso della lotteria (EV) è la media delle vincite
nei due casi (M=9 e M=27) ponderata per le probabilità che i due eventi si veri…chino
quindi
EV = 12 (9) + 12 (27) = 18
Aldo può scegliere tra una somma …ssa di 12 euro o una lotteria il cui valore atteso
è pari a 18 (superiore alla somma certa). Se Aldo è neutrale al rischio sceglie sicuramente la lotteria.
Vero/ Falso 15. Si consideri una lotteria che promette due vincite monetarie (M)
1 e 100, ciascuna con probabilità 12 . Se un soggetto ha la funzione di utilità U(M) =
p
M allora l’utilità attesa della lotteria per quel soggetto e 5,5.
Soluzioni. VERO. L’utilità attesa di una lotteria (EU) è la media delle utilità nei due casi (M=1 e M=100) ponderata per le probabilità che i due eventi si
veri…chino quindi
p
p
EU = 12 1 + 21 100 = 0; 5 + 5 = 5; 5
Vero/Falso 16. Si consideri una lotteria che promette due vincite monetarie (M)
1 e 10, ciascuna con probabilità 21 . Se un soggetto ha la funzione di utilità U(M)=M2
allora l’utilità attesa della lotteria per quel soggetto e 50,5.
Soluzioni. VERO. L’utilità attesa di una lotteria (EU) è la media delle utilità
nei due casi (M=1 e M=10) ponderata per le probabilità che i due eventi si veri…chino
quindi
EU = 12 12 + 12 102 = 0; 5 + 50 = 50; 5
5
Vero/Falso 17. Tontolo può scegliere tra una vincita certa di 5 euro o una lotteria.
Partecipando alla lotteria Tontolo potrebbe vincere zero, 6 o 9 euro (M0 = 0; M1 =
6; M2 = 9). Ciascun esito ha probabilità 1/3 . Sapendo che Tontolo ha accettato di
partecipare alla lotteria perché giocando ottiene un’utilità maggiore, ne concludiamo
che la sua funzione di utilità è U(M)=Ma con a <1.
Soluzioni. FALSO. Il valore atteso della lotteria (EV) è la media delle vincite
nei tre stati del mondo ponderata per le probabilità che i tre eventi si veri…chino
quindi
EV = 13 0 + 13 6 + 13 9 = 2 + 3 = 5
Se l’individuo preferisce la lotteria ad una somma certa il cui valore è lo stesso della
lotteria, allora l’individuo sarà amante del rischio. Un individuo amante del rischio
si caratterizza per una funzione di utilità convessa ovvero del tipo U(M)=M a con
a>1.
Vero/Falso 18. Ugo può acquistare per 35 euro il biglietto di una lotteria che
promette una vincita nulla, di 27 o di 81 euro. Ciascun esito ha probabilità 1/3. Se
Ugo fosse amante del rischio sceglierebbe di acquistare il biglietto.
Soluzioni. VERO. Il valore atteso della lotteria (EV) è la media delle vincite
nei tre stati del mondo ponderata per le probabilità che i tre eventi si veri…chino
quindi
EV = 13 0 + 13 27 + 13 81 = 36
Se l’individuo è amante del rischio preferisce una lotteria che in media paga 36 euro
ad una somma certa di 36 euro; in questo caso dove addirittura gli si o¤ re la possibilità di scegliere tra una somma certa di 35 ed una lotteria che in media paga 36
sceglierà sicuramente la lotteria ed acquisterà il biglietto.
Vero/Falso 19. Un individuo propenso al rischio non acquisterà mai il biglietto di
una lotteria equa.
Soluzioni. FALSO. Una lotteria è equa se il prezzo per partecipare a tale lotteria è pari alla vincita attesa della lotteria. Una lotteria equa consente quindi ad
un individuo di scambiare una ricchezza certa pari ad X (dove X indica il generico
prezzo del biglietto della lotteria) in una prospettiva incerta avente valore atteso pari
ad X. Poichè un individuo propenso al rischio tra due lotterie aventi il medesimo
valore atteso sceglie sempre quella a maggior varianza (ovvero che si caratterizza per
un maggior livello di rischio), un individuo amante del rischio sceglierà sicuramente
di acquistare il biglietto di una lotteria equa.
Vero/Falso 20. Sul mercato delle automobili usate vengono vendute sia auto di
qualità che catorci. Gli acquirenti tipo, la cui disponibilità a pagare è riportata nella
tabella sottostante unitamente al prezzo di riserva dei venditori, non sono in grado
di distinguere i due tipi di auto. Supponete inoltre che l’acquirente tipo sia neutrale
al rischio.
6
Disponibilità a pagare di un acquirente tipo2
Prezzo di riserva dei venditori3
Auto di qualità
3000
3000
Catorci
1000
2000
Sapendo che tra le auto in vendita ci sono dei catorci, non si veri…cheranno scambi.
Soluzioni. VERO. Un individuo neutrale al rischio non è disposto a pagare un
prezzo superiore al valore del bene che si accinge ad acquistare dunque nel caso in
esame per un’auto di cui non riconosce la qualità sarà disposto a pagare al massimo
un prezzo pari a 3000p + 1000(1 p) dove p indica la probabilità che l’auto sia
di qualità e (1-p) la probabilità che si tratti di un catorcio. Inoltre, poichè 3000p +
1000(1 p) < 3000 ovvero poichè la massima disponibilità a pagare dell’acquirente tipo
con informazione asimmetrica risulta inferiore al prezzo di riserva dei venditori di
auto di qualità, a tale prezzo il solo bene che l’acquirente tipo potrebbe acquistare è un
catorcio. Dunque l’acquirente tipo, nonostante il problema di asimmetria informativa
è consapevole che pagando un prezzo non superiore a 3000p + 1000(1 p) potrà
acquistare esclusivamente un catorcio. Ma per un catorcio l’acquirente tipo sarebbe
disposto a pagare al massimo 1000 e tale disponibilità a pagare risulta inferiore al
prezzo di riserva dei venditori di catorci; quindi se vi è una probabilità positiva di
acquistare un catorcio e gli acquirenti non sono in grado di distinguere le auto di
qualià, non si veri…cheranno scambi.
2 Indica
3 Indica
il prezzo massimo ch l’acquirente tipo sarebbe disposto a pagare per ciascun quadro.
il prezzo minimo a cui il venditore tipo sarebbe disposto a vendere ciascun quadro.
7
3
C - Esercizi.
Si risolvano i seguenti esercizi. Per ogni esercizio corretto vengono attribuiti 10 punti.
Esercizio 1. La Medium Job fa settimanalmente colloqui di lavoro per assumere
i dipendenti del suo nuovo stabilimento. I candidati si presentano tutti vestiti allo
stesso modo e con lo stesso curriculum, ma metà di essi sono più e¢ cienti degli altri.
La Medium Job sa questa cosa ma non riesce in alcun modo a distinguere tra le due
tipologie di candidati.
1. Discutete il problema fronteggiato dalla Medium Job e rappresentate questa
situazione con le categorie economiche che conoscete.
2. L’incapacità di distinguere tra le tipologie di candidati incida sui contratti
o¤erti dalla Medium Job? In che modo? Rispondete alla domanda speci…cando
le di¤erenze tra quanto vi aspettate che accada nella situazione qui descritta e
quanto si veri…cherebbe se la Medium Job riuscisse a distinguere i candidati.
3. Quale soluzione potrebbero ideare la Medium Job e i candidati più e¢ cienti
per tentare di risolvere il problema discusso al punto precedente?
Soluzioni. (1) Questo è chiaramente un problema di informazione asimmetrica, in particolare di informazione nascosta. Una delle due parti dello scambio
(l’acquirente, Medium Job) è meno informata dell’altra (i candidati) circa la qualità dell’oggetto che si sta per scambiare (l’e¢ cienza delle prestazioni lavorative). La
prima parte (Medium Job) ottiene risultati diversi a seconda della qualità dell’oggetto
scambiato (lavoro), ma non è in grado di conoscere tale qualità, a di¤ erenza dell’altra
parte, verosimilmente a causa di un comportamento di coloro che sono caratterizzati da qualità bassa (bassa e¢ cienza). Da non confondere il caso di con “azione
nascosta” (asimmetria di informazione sul comportamento tenuto da una delle parti
durante l’esecuzione di un contratto).
(2) Se la Medium Job potesse distinguere i candidati, sarebbe disposta a pagare di
più i lavoratori più e¢ cienti: si formerebbero due mercati separati per le due qualità,
e sul mercato della qualità migliore sia la curva di domanda sia quella d’o¤ erta sarebbero spostate più in alto rispetto all’altro mercato, con un conseguente maggior prezzo
di equilibrio. Non potendo distinguere i candidati, per ogni diversa quantità di lavoro
la Medium Job sarà disposta ad o¤ rire una paga pari ad una media ponderata fra il
prezzo alto e quello basso che vorrebbe pagare in caso di informazione simmetrica: i
pesi della media sono inizialmente 1/ 2 e 1/ 2, poiché Medium Job sa che questa è la
proporzione dei due tipi. In altri, termini, la Medium Job si presenta sui due mercati
con la medesima curva di domanda. Ma ora i lavoratori più e¢ cienti si o¤ riranno in
minor numero, perché si vedono o¤ rire una paga inferiore a quella che avrebbero nel
caso di informazione simmetrica. In maniera simmetrica i lavoratori meno e¢ cienti
si o¤ riranno in maggior numero, perché si vedono o¤ rire una paga superiore a quella
che avrebbero nel caso di informazione simmetrica. Dunque le proporzioni dei due
tipi di lavoratori assunti cambiano, a favore della quota dei meno e¢ cienti: se, dopo
aver sperimentato l’e¤ ettiva qualità dei suoi lavoratori, la Medium Job deduce che la
probabilità di trovare lavoratori e¢ cienti è inferiore a 1/ 2, la settimana successiva
abbasserà la paga o¤ erta. Procedendo così, sul mercato potrebbero rimanere solo lavoratori poco e¢ cienti e con paga bassa (“selezione avversa”): è scomparso il mercato
8
dei lavoratori più e¢ cienti, e con esso il relativo surplus sociale, che sarebbe invece
esistito in caso di informazione simmetrica.
(3) E’ interesse dei lavoratori più e¢ cienti convincere la Medium Job di essere
tali. Un modo ‘economicamente’e¢ cace per fornire una ‘garanzia’alla Medium Job
è essere disposti ad accettare un contratto in cui, per esempio, vengono inizialmente
pagati con paga elevata, ma poi accetteranno un’ampia riduzione di paga (scendendo
sotto la paga di un lavoratore non e¢ ciente) se si scopre che non sono e¢ cienti.
I lavoratori non e¢ cienti non accetterebbero un contratto di questo tipo, in quanto
sono certi che dovranno poi accettare una paga inferiore al loro valore. Accettare quel
contratto è dunque un ‘segnale’ credibile di qualità elevata.
Esercizio 2. Si discuta del modello di scelta sotto incertezza. In particolare:
1. si de…niscano le nozioni di variabile casuale, o lotteria, valore atteso e varianza,
spiegando quali caratteristiche del problema di scelta le due ultime misurano;
2. si de…nisca la nozione avversione al rischio, usando solo le nozioni individuate
al punto precedente e senza fare gra…ci;
3. si de…nisca la nozione di utilità attesa; utilizzando il “principio dell’utilità attesa”, si dimostri che una funzione di utilità concava rappresenta e¤ettivamente
le preferenze di un avverso al rischio.
Soluzioni. (1) Si parla di scelta sotto incertezza quando gli esiti delle proprie
scelte non sono noti con certezza nel momento in cui le si prende, vale a dire che
dopo aver compiuto una scelta interviene ancora qualche evento casuale in grado
di in‡uenzare l’esito. L’esito stesso, dunque, può essere visto come una variabile
casuale, cioè una variabile che potrà assumere uno tra un certo numero di valori,
ciascuno con una certa probabilità. La probabilità di ognuno dei valori è un numero
compreso fra zero e uno; una probabilità maggiore indica che c’è maggior …ducia che
nella possibilità che quel valore si veri…chi. Una lotteria è una variabile casuale i cui
valori sono somme monetarie. Il valore atteso (VA) di una lotteria è il valore che in
media ci si aspetta di vincere, e si calcola come media ponderata dei diversi valori,
con pesi dati dalle corrispondenti probabilità. La varianza di una lotteria misura il
suo rischio, vale a dire il fatto che con quella lotteria si possa vincere molto ma anche
perdere molto; la varianza è la media ponderata (con le probabilità) delle distanze al
quadrato dei diversi esiti dal loro valore atteso.
(2) Si dice avverso al rischio un soggetto che fra due lotterie con il medesimo
valore atteso preferisce quella con minor varianza.
(3) Se un soggetto può fruire di una certa somma monetaria, per valutare il suo
benessere non usiamo la somma monetaria, ma l’utilità che quel soggetto ricava dalla
somma monetaria stessa. Una funzione di utilità è una funzione che dice qual è il
livello di utilità (un numero) che corrisponde al possesso di ogni possibile somma
monetaria. È ragionevole supporre che una funzione di utilità sia crescente. Allora,
un soggetto che a¤ ronta una lotteria è interessato non tanto alle somme monetarie
che potrà ottenere quanto alle utilità che ne deriveranno. Ecco allora che la variabile
casuale che davvero interessa a quel soggetto è in termini di utilità: una variabile casuale con valori pari alle utilità delle diverse somme monetarie, e con probabilità pari
alle corrispondenti somme monetarie stesse. Essendo l’utilità una variabile casuale,
se ne può calcolare il valore atteso, che si chiama utilità attesa (UA). Il principio
9
dell’utilità attesa a¤ erma che ogni soggetto, di fronte a diverse lotterie, sceglie quella
che gli dà massima utilità attesa. Se la funzione di utilità di un individuo è concava,
gli archi giacciono sopra la corrispondente corda (vedi gra…co)
U
U(A)
U(VA)
UA
U(B)
B
VA
M
A
In questo caso l’individuo preferisce strettamente disporre con certezza della somma
VA piuttosto che partecipare ad una lotteria con analogo valore atteso; infatti
U (V A) > U A
Dato che la varianza associata all’opzione "disporre con certezza della somma VA" è
nulla mentre la varianza associata all’opzione "partecipare ad una lotteria con esito
atteso VA" è positiva, l’individuo è e¤ ettivamente avverso al rischio.
p
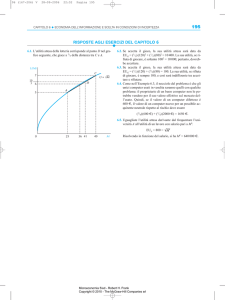
Esercizio 3. La funzione di utilità di Antonio è data da U (X) = Xdove X indica
il reddito percepito. Antonio ha due possibilità lavorative: diventare un impiegato
di banca ed ottenere 100 euro/ora; avviare un’attività in proprio ed ottenere 400
euro/ora nel 20% dei casi (25 euro/ora altrimenti).
1. Caratterizzate l’atteggiamento di Antonio rispetto al rischio e calcolate il reddito orario che Antonio si aspetta di ottenere nelle due opzioni lavorative.
2. De…nite e calcolate l’utilità attesa di Antonio in corrispondenza delle due opzioni
lavorative. In base ai risultati ottenuti, quale carriera verrà scelta?
3. Mario è neutrale al rischio mentre Alberto è amante del rischio. Qualora venissero loro o¤erte le medesime opzioni lavorative presentate ad Antonio, cosa
deciderebbero di fare? Argomentate la risposta.
Soluzioni. (1) Dal momento che Antonio si caratterizza per una funzione di
utilità crescente e concava,
dU (X)
dX
= 21 X
0:5
> 0e
d2 U (X)
(dX)2
=
1
4X
1:5
< 0;
egli è avverso al rischio. Nel caso in cui scelga la prima opzione lavorativa Antonio
otterrà con certezza 100 euro/ora. Il valore atteso del reddito in corrispondenza della
seconda opzione è invece
EV2 = (400)
20% + 25
10
80% = 80 + 20 = 100
(2) L’utilità attesa associata alle due opzioni lavorative è
EU1 = U (100) = 10
EU2 = U (400)
20% + U (25)
80% = 4 + 4 = 8
Dato che EU1 > EU2 Antonio preferirà la carriera di impiegato di banca. Trattandosi
di individua avverso al rischio, dovendo scegliere tra due lotterie caratterizzate dal
medesimo valore atteso sceglie sempre quella a minor varianza.
(3) Dato che le due carriere si caratterizzano per il medesimo valore atteso, gli
individui neurali al rischio, come Mario, saranno indi¤ erenti tra le due prospettive
lavorative mentre quelli amanti del rischio, come Antonio, preferiranno certamente
la seconda prospettiva alla prima.
Esercizio 4. Nel Paese A ci sono due gruppi di consumatori
p (gruppo 1 e gruppo 2)
caratterizzati dalla medesima funzione di utilità U (M ) = M , dove M = 36 euro è
il livello iniziale di ricchezza di ciascun consumatore. Entrambi i gruppi sono esposti
ad una perdita di 20 euro ma la stessa si veri…cherà nel 50% dei casi per i consumatori
del primo gruppo e solo nel 10% dei casi per quelli del secondo gruppo.
1. Come si può caratterizzare l’atteggiamento dei due gruppi di consumatori
rispetto al rischio? Calcolate il valore atteso e l’utilità attesa per le due categorie di consumatori.
2. Fornite una rappresentazione gra…ca della funzione di utilità dei due gruppi di
consumatori e riportate i valori calcolati al punto precedente.
3. Qual è la massima cifra che i consumatori appartenenti al primo gruppo sono
disposti a versare per assicurarsi integralmente contro il rischio di subire la
perdita? Vi aspettate che i consumatori del secondo gruppo siano disposti a
versare la stessa cifra, una cifra maggiore o una cifra inferiore? Argomentate
la risposta.
Soluzioni. (1)-(2) Dal momento che i due gruppi di consumatori si caratterizzano per la medesima funzione di utilità e che la suddetta risulta crescente e concava,
dU (M )
dM
= 12 M
0:5
> 0e
d2 U (M )
(dM )2
=
1
4M
1:5
< 0;
si tratta di individui avversi al rischio. Il valore atteso (EV) è de…nito come a somma
di tutti i possibili risultati di una lotteria, ponderata in funzione delle rispettive probabilità di veri…carsi. Per quanto concerne il primo gruppo di consumatori, essi si
attendono una ricchezza pari a
EV1 = (M
20)
50% + M
50% = 36
10 = 26
90% = 36
2 = 34
mentre il secondo gruppo di consumatori
EV2 = (M
20)
10% + M
Con riferimento all’utilità attesa, il primo gruppo di consumatori ha
EU1 = U (M
20)
50% + U (M )
11
50% = 2 + 3 = 5
mentre il secondo
EU2 = U (M
20)
10% + U (M )
90% =
2
5
+
27
5
=
29
5
Gra…camente
U(M)
Funzione di
utilità
6
EU2
EU1
4
16
EV1
EV2 36
M
(3) Dal momento che i consumatori del primo gruppo otterrebbero un’utilità pari
ad EU1 avendo a disposizione con certezza una somma pari a 25
p
EU1 = U (X) ) 5 = X ) X = 25;
ne consegue che saranno disposti a versare …no ad un massimo di 11 euro
M
X = 36
25 = 11
per assicurarsi contro il rischio di perdite. Tale assicurazione infatti garantirà loro
una ricchezza disponibile pari a 25 in qualunque stato del mondo.
(4) Pur essendo caratterizzati dalla medesima avversione al rischio, i consumatori del secondo gruppo sono meno esposti al rischio di perdite; conseguentemente la
somma massima che saranno disposti a versare per un’assicurazione contro il rischio
di perdite sarà certamente inferiore a quella trovata al punto 3.
Esercizio 5. Il signor Pavido possiede una ricchezza iniziale W=15, ma quest’anno
potrebbe evadere le tasse ottenendo un incremento di ricchezza pari a 8. Se però
venisse scoperto, fermo restando l’aumento di ricchezza, subirebbe una multa pari a
16. La probabilità di essere scoperto è 43 . Le preferenze di Pavido per la ricchezza
sono rappresentate dalla funzione di utilità U(W) =W2 :
1. Rappresentare in un opportuno gra…co la funzione di utilità di Pavido, il livello
di utilità derivante dalla ricchezza iniziale (W=15), e l’utilità attesa derivante
dall’evasione. Determinate se Pavido sceglie di evadere o meno.
2. Rappresentate sul medesimo gra…co l’equivalente certo della scelta di evadere
da parte di Pavido, e il suo premio per il rischio.
3. Supponete ora che la multa che Pavido deve pagare se la sua evasione è scoperta
sia 8, e non 16: la scelta di Pavido cambia? Perché?
12
Soluzioni (1). L’utilità derivante dalla ricchezza iniziale, cioè nel caso di non
evasione è 152 = 225: Se Pavido evade può …nire con ricchezza …nale 23 oppure 7,
con probabilità rispettivamente 14 e 43 (come visto prima, la ricchezza attesa EV è
11). Le utilità dei due casi sono 23 2 =529 e 7 2 =49, per cui l’utilità attesa in caso
di evasione è
3
1
+ 49
= 169 :
EU = 529
4
4
L’utilità attesa nel caso in cui Pavido decida di evadere è inferiore a quella associata
allìevasione; quindi Pavido, pur essendo propenso al rischio, deciderà di non evadere.
Gra…camente:
(2) L’equivalente certo di una situazione incerta è il livello di ricchezza che, se
posseduto con certezza, darebbe al decisore la medesima utilità della situazione incerta. Nel nostro caso l’utilità attesa della situazione incerta (evadere) è 169, e
dunque l’equivalente certo è una cifra CE tale che U(CE) = 169, cioè CE 2 = 169,
da cui CE = 13. Il premio per il rischio relativo ad una certa situazione incerta è la
di¤ erenza fra il suo valore atteso EV e il suo equivalente certo CE, quindi nel nostro
caso è EV-CE = 11-13 = -2. Si veda il gra…co precedente.
(3) Se la multa fosse 8, in ogni caso la ricchezza minima con cui Pavido potrebbe
rimanere sarebbe 15 (se evadendo fosse scoperto). Dunque i due livelli di utilità in
caso di evasione sarebbero 15 2 =225 e 23 2 =529, la cui media (EU) è comunque maggiore di 225, l’utilità di non evadere. Quindi evaderebbe.
Esercizio 6. Il signor Ardito possiede una ricchezza iniziale W=169, ma quest’anno
potrebbe evadere le tasse ottenendo un incremento di ricchezza pari a 120. Se però
venisse scoperto, fermo restando l’aumento di ricchezza, subirebbe una multa pari a
240. La probabilità di essere scoperto è 12 . Le preferenze di Ardito per la ricchezza
sono rappresentate dalla funzione di utilità U(W) =W0:5 .
1. Rappresentare in un opportuno gra…co la funzione di utilità di Ardito, il livello
di utilità derivante dalla ricchezza iniziale (W=169), e l’utilità attesa derivante
dall’evasione. Determinate se Ardito sceglie di evadere o meno.
2. Rappresentate sul medesimo gra…co l’equivalente certo della scelta di evadere
da parte di Ardito, e il suo premio per il rischio.
3. Supponete ora che la multa che Ardito deve pagare se la sua evasione è scoperta
sia 120, e non 240: la scelta di Ardito cambierebbe, e perché?
13
p
Soluzioni. (1) L’utilità derivante dalla ricchezza iniziale è 169 = 13. Come
argomentato sopra, questa è anche l’utilità del valore atteso (EV) della “lotteria” di
evadere. Se evade potrebbe …nire con ricchezza …nale 169+120=289
oppurep169+120p
240=49, con probabilità 12 : le utilità in questi due casi sono 289=17 e 49=7 per
cui l’utilità attesa in caso di evasione è
EU = 17
1
+ 7
2
1
= 12 :
2
Dunque l’utilità attesa in caso di evsione è inferiore a quella in caso di non evasione.
Gra…camente
(2) L’equivalente certo di una situazione incerta è il livello di ricchezza che, se
posseduto con certezza, darebbe al decisore la medesima utilità della situazione incerta. Nel nostro caso l’utilità attesa della situazione incerta (evadere)
è 12, e dunque
p
l’equivalente certo è una cifra CE tale che U(CE) = 12, cioè CE = 12, da cui CE
= 144. Il premio per il rischio relativo ad una certa situazione incerta è la di¤ erenza
fra il suo valore atteso EV e il suo equivalente certo CE, quindi nel nostro caso è
EV-CE = 169-144 = 15. Si veda il gra…co precedente.
(3) Se la multa fosse 120, in ogni caso la ricchezza minima con cui Ardito potrebbe
rimanere sarebbe 169 (se evadendo
fosse p
scoperto). Dunque i due livelli di utilità in
p
caso di evasione sarebbero 289=17 e 169=13, la cui media (EU) è comunque
maggiore di 13, l’utilità di non evadere. Quindi evaderebbe.
Esercizio 7. Esistono due qualità di bulbi di tulipano: qualità alta e bassa. Il
costo marginale di produzione (lineare crescente in entrambi i casi [cioè le curve di
o¤erta sono crescenti e lineari]) e la disponibilità a pagare (lineare decrescente in
entrambi i casi [cioè le curve di domanda sono decrescenti e lineari]), sono maggiori
per la qualità alta che per quella bassa.
1. Individuate l’equilibrio dei due mercati nel caso di informazione simmetrica.
2. Immaginate invece che i consumatori non sappiano distinguere la qualità dei
bulbi che stanno per acquistare, ma che lo scoprano solo dopo la …oritura. Essi
sanno che i bulbi possono essere sia di alta sia di bassa qualità, e inizialmente
ritengono che la probabilità di trovarne uno buono sia 21 . Spiegate che problema
si crea, e come si modi…ca l’equilibrio dei mercati rispetto al punto precedente.
14
3. Dite cosa possono fare i venditori di bulbi di buona qualità per risolvere il problema di cui al punto precedente.
Soluzioni. (1) Dalla descrizione precedente, e dai commenti tra le parentesi
quadre, ricaviamo facilmente i gra…ci per i due mercati:
Il gra…co di sinistra rappresenta il mercato della qualità alta, dove o¤ erta e domanda
(rispettivamente S A e D A ) sono curve più alte rispetto a o¤ erta e domanda del gra…co
di destra (rispettivamente S B e D B ). Le quantità di equilibrio sui due mercati sono,
rispettivamente, X e Y; il prezzo di equilibrio della qualità alta è maggiore di quello
della qualità bassa.
(2) È il caso tipico di informazione nascosta. Non potendo distinguere le qualità, i consumatori saranno disposti a pagare, per ogni bulbo, un prezzo intermedio
(esattamente a metà, data l’ipotesi sulle probabilità pari a 1/2) fra il prezzo alto e
quello basso che pagherebbero per le due qualità sa sapessero individuarle. Dunque su
entrambi i mercati esiste ora una sola curva di domanda D M , intermedia fra la D A
e la D B dei due precedenti mercati. Come si vede dal gra…co successivo, le quantità
di equilibrio si modi…cano
Infatti, la domanda che si presenta sul primo (secondo) mercato è ora più bassa
(alta) di prima, e dunque la quantità di equilibrio del primo (secondo) mercato è ora
inferiore (superiore) a prima. Questo cambiamento induce i consumatori a pensare
che ora la probabilità di trovare un bulbo di bassa qualità sia maggiore, e dunque
15
la curva di domanda intermedia D M si sposta ulteriormente verso il basso, facendo
diminuire la quantità di equilibrio su entrambi i mercati. Ma sul mercato della bassa
qualità la quantità scambiata in proporzione si riduce meno che sull’altro mercato
(provare sul gra…co per credere), e dunque la proporzione di bulbi di bassa qualità
scambiati aumenta ulteriormente, facendo ancora abbassare la curva D M . Il fenomeno continua sino al punto in cui la D M si sposta così in basso che sul mercato della
qualità alta non si scambiano più bulbi. Questo problema è noto come problema di
selezione avversa: solo i bulbi di bassa qualità vengono scambiati.
(3) Possono chiedere un prezzo elevato, ma o¤ rendo in cambio una garanzia: se,
una volta …orito, il tulipano sarà brutto gli acquirenti verranno rimborsati (magari
con gli interessi). Siccome per i venditori della bassa qualità non è conveniente o¤ rire
tale garanzia, visto che di sicuro il tulipano sarà brutto, ecco che questo meccanismo
di segnalazione può risolvere il problema e ristabilire un esito analogo a quello che si
aveva in presenza di informazione simmetrica.
Esercizio 8. Nel mercato concorrenziale dei quadri vengono venduti sia quadri
autentici che riproduzioni. L’acquirente tipo, che non è in grado di distinguere tra
i due prodotti, ritiene che solo il 20% dei quadri in vendita siano autentici e che il
restante 80% siano riproduzioni. In tabella sono riportate le disponibilità a pagare
ed i prezzi di riserva per un quadro autentico e per una riproduzione.
Disponibilità a pagare di un acquirente tipo4
Prezzo di riserva dei venditori5
Quadro autentico
2000
600
Riproduzioni
400
100
1. Supponendo che l’acquirente tipo sia neutrale al rischio e che il prezzo di mercato sia pari alla massima disponibilità a pagare dei consumatori, calcolate il
prezzo di vendita dei quadri.
2. Supponete ora che i rivenditori di quadri autentici (ma non quelli di riproduzioni) possano acquistare un certi…cato di qualità attestante l’autenticità del
quadro venduto, quale prezzo massimo dovrebbe avere tale certi…cazione per
essere e¢ cace? In questo caso i consumatori pagherebbero 2000 per un quadro
certi…cato (ritenendo che tale quadro sia autentico) e 400 per uno non certi…cato
(ritenendo che tale quadro sia una riproduzione).
3. Se il certi…cato di qualità di cui al punto (2) comportasse un costo aggiuntivo per i venditori di quadri autentici pari a 1100, si tornerebbe all’e¢ cienza
dell’informazione perfetta? Argomentate.
Soluzioni. (1) Un individuo neutrale al rischio non è disposto a versare una
somma superiore al valore atteso del bene che si accinge ad acquistare. Nel caso
in esame quindi il prezzo massimo che l’acquirente tipo è disposto a pagare per un
quadro di cui non distingue la qualità è
2000
20% + 400
80% = 400 + 320 = 720;
dunque in caso di informazione asimmetrica i quadri (sia quelli autentici che le riproduzioni) saranno in vendita ad un prezzo pari a 720. Da notare che tale prezzo risulta
4 Indica
5 Indica
il prezzo massimo ch l’acquirente tipo sarebbe disposto a pagare per ciascun quadro.
il prezzo minimo a cui il venditore tipo sarebbe disposto a vendere ciascun quadro.
16
superiore sia al prezzo di riserva dei venditori di riproduzioni che a quello dei venditori di quadri autentici; dunque entrambi hanno interesse a vendere il loro prodotto.
(2) La certi…cazione di qualità consente ai venditori di quadri autentici di farsi
riconoscere e di ottenere un prezzo di 2000. D’altronde il segnale comporta un costo
addizionale per i rivenditori di quadri autentici quindi è necessario che il costo della
segnalazione non risulti eccessivamente elevato. Formalmente è necessario che
2000
600
C
0!C
1400
dove C indica il costo della certi…cazione.
(3) Nel caso in cui la certi…cazione comportasse per i venditori di quadri autentici
un costo addizionale di 1100, i venditori di quadri autentici avrebbero interesse ad
utilizzare la certi…cazione come segnale e si tornerebbe ad una situazione simile a
quella con informazione perfetta. I consumatori infatti riconoscerebbero, per merito
della certi…cazione, i quadri autentici (venduti con il certi…cato di autenticità) dalle
riproduzioni; d’altra parte non si tornerebbe all’e¢ cienza dell’informazione perfetta
in quanto la segnalazione comporta dei costi che non sarebbero stati necessari con
informazione perfetta.
17