Lezioni 26-27 marzo 2013 (parte a)

Capitolo 6
Economia dell’informazione e
scelta in condizioni di incertezza
ECONOMIA DELL’INFORMAZIONE
L’informazione è un fattore importante
nel processo decisionale di
consumatori e imprese
Nella realtà, il più delle volte le scelte
degli agenti economici sono prese in
condizioni di informazione non
perfetta ovvero di informazione
asimmetrica
ECONOMIA DELL’INFORMAZIONE (2)
 In presenza di informazione asimmetrica tra
“parti” con interessi contrapposti che possiamo
chiamare principale e agente (es.
acquirente/venditore, datore di lavoro/lavoratore/,
assicuratore/assicurato) può emergere il rischio di
“azzardo morale” o “selezione avversa”.
 Azzardo morale: il rischio che l’agente tenda ad
avere un comportamento inadeguato – negligente
o fraudolento - che “danneggia” il principale e può
portare al malfunzionamento dei mercati.
 Selezione avversa: la presenza di asimmetria
informativa limita la partecipazione a scambi
volontari a soggetti che possiedono “qualità”
meno desiderabili
ECONOMIA DELL’INFORMAZIONE:
Selezione avversa
 Un esempio classico di selezione avversa è il
cosiddetto mercato dei bidoni (auto di cattiva
qualità)
 In questo mercato l’asimmetria informativa aiuta a
spiegare perché un’auto quasi nuova ma usata valga
molto meno di una nuova
 Se avete un’auto usata di alta qualità dovrete venderla
ad un prezzo medio rappresentativo di tutte le qualità
presenti;
 Ma allora potreste ritirarvi dal mercato e questo
farebbe scendere ulteriormente la qualità media e il
prezzo dei compratori;
 (altri esempi) assicurazione, rapporto di lavoro
Selezione avversa: I rimedi del mercato (e
dello Stato)
 Il problema di funzionamento del mercato risiede nel
“vizio originario”, l’asimmetria informativa.
 Talvolta i mercati stessi possono trovare meccanismi
risolutivi che consentono di ristabilire la “simmetria
dell’informazione” attraverso dei segnali credibili in
grado di rivelare le informazioni private alla parte
non informata
 Talvolta è lo Stato che può regolare il mercato
attraverso leggi o regolamentazione (es. sistema
sanitario pubblico al posto di polizze private al fine di
garantire a tutti i cittadini un adeguato livello di
assistenza sanitaria)
ECONOMIA DELL’INFORMAZIONE:
Segnalazione (dalla parte informata)
 Affinché un messaggio da parte di un potenziale
avversario risulti credibile, non deve esservi alcuna
convenienza a simularlo
 Il principio della non convenienza a simulare
afferma che, affinché una segnalazione ad un
avversario risulti credibile, deve essere costoso
simularla (es. pubblicità in TV: costi elevati e non
recuperabili; garanzie sui prodotti)
 Sulla base del principio della completa
comunicazione se un segnale è informativo gli
individui devono comunicare anche le qualità a
loro sfavorevoli (anche implicitamente)
Segnalazione: il mercato delle auto (studio
sperimentale di Tadelis e Zettelmeyer)
• 8000 auto in vendita all’asta su eBay
divise in 2 gruppi:
• Gruppo 1: asta con informazioni standard
(anno, km, percorsi);
• Gruppo 2: asta con informazioni molto
dettagliate (condizioni interni,
carrozzeria).
Analisi delle (i) probabilità di vendita; (ii)
prezzo di vendita.
Risultati: le macchine del secondo gruppo presentavano
migliori probabilità di vendita e prezzi più alti.
In particolare le auto in peggiori condizioni del secondo
gruppo. Perché?
I compratori erano in grado di identificare in modo più
“certo” le auto preferite con conseguente aumento
della concorrenza tra acquirenti anche per le
macchine peggiori.
Tuttavia alcuni studi dimostrano che un “eccesso di
informazione” potrebbe essere controproducente .(es.
studio di Tadelis su nuovi utenti delle aste eBay)
Figura 6-1: Informazione implicita nel silenzio
Il Gracidio basso è un segnale positivo. Supponiamo che un
gracidio sotto ‘6’ sia sufficiente. Non gracidare significa essere
sopra la soglia. Se non gracidi ti verrà attribuito un valore medio
(8). Ma allora se sei tra 6 e 8…..
ECONOMIA DELL’INFORMAZIONE:
Screening (dalla parte non informata)
 Talvolta è la parte non informata ad intraprendere
azioni volte a ottenere maggiori informazioni
 Esistono numerosi meccanismi di screening. Ad
esempio una compagnia assicurativa può applicare
polizze differenti al fine di “isolare” i contraenti più
rischiosi da quelli meno rischiosi (tariffe più elevate
a copertura totale + tariffe scontate con franchigie
più elevate). Un datore di lavoro può richiedere ai
laureati “test” addizionali se il voto di laurea non
rappresenta un segnale “adeguato”.
Es. di meccanismo di Screening ne mercato
assicurativo: la “scatola nera” in auto
Voto medio dei laureati in Economia
Aziendale nel 2010 in alcune Università
Italiane
• Economia Aziendale:
Bari:
104/110;
Venezia:
95,1/110;
Catania:
97/110;
La Sapienza Roma: 100/110
SCELTA IN CONDIZIONI DI
INCERTEZZA
 La maggior parte delle scelte viene effettuata in
condizioni di incertezza, non consociamo con certezza
gli esiti di certe scelte -al massimo possiamo conoscere
gli eventi che possono verificarsi (e il nostro payoff in
ogni evento) e le probabilità con cui si verificano. Con
queste informazioni è possibile calcolare i valori attesi
associati ad una scelta (EV = Expected value)
 L’analisi delle scelte in presenza di incertezza è
effettuata utilizzando il modello dell’utilità attesa di
von Neumann e Morgenstern
 In questo modello si applica una funzione di utilità che
assegna un valore numerico alla soddisfazione
associata ad ogni possibile evento e payoff associato
SCELTA IN CONDIZIONI DI
INCERTEZZA
 Date 2 lotterie:
EV1  p1M0  A 1 p1M0  B
EV2  p2M0 C 1 p2M0  D
 Il modello di von Neumann e Morgenstern
asserisce che un consumatore razionale, posto a
scegliere tra alternative incerte, effettua le proprie
scelte in modo da massimizzare l’utilità attesa (e non
il valore atteso)
 Il punto cruciale della teoria è che l’ordinamento dei
valori attesi di un insieme di contesti di scelta
incerta è spesso diverso dall’ordinamento delle
utilità attese delle alternative considerate
SCELTA IN CONDIZIONI DI
INCERTEZZA
Valore atteso= media dei risultati
della lotteria ponderata con le
probabilità di ogni risultato
VA=∑i(piVi)
Utilità attesa= media ponderata delle
utilità associate con ogni risultato
UA=∑i(pi U(Vi))
SCELTA IN CONDIZIONI DI
INCERTEZZA: Avversione al rischio
Una lotteria è detta equa se il suo valore
atteso, cioè la somma di tutti i possibili
esiti ponderata dalla probabilità che essi
hanno di verificarsi, è pari a zero
Una funzione di utilità concava indica un
individuo avverso al rischio (ossia un
individuo che rifiuta di partecipare ad una
lotteria equa)
Figura 6-2: Funzione di utilità concava (derivata seconda negativa)
Come è l’utilità marginale?
Figura 6-3: Un individuo avverso al rischio rifiuterà sempre un gioco equo
Dotazione =40; Accettereste una
scommessa che vi attribuisce 70
o 10 con probabilità ½, in
cambio della dotazione?
U (40)=32
U (G. equo)=28=1/2*18+1/2*38
SCELTA IN CONDIZIONI DI
INCERTEZZA
Una funzione di utilità convessa indica
un individuo propenso al rischio (ossia
un individuo che accetta di partecipare
ad una lotteria equa)
Una funzione di utilità lineare indica un
individuo neutrale rispetto al rischio
(ossia un individuo che è indifferente tra
l’accettare o il rifiutare di partecipare ad
una lotteria equa)
Figura 6-4: La funzione di utilità di un individuo propenso al rischio è
convessa rispetto alla richezza totale
U(M0)<EUG
Figura 6-5: Neutralità rispetto al rischio
Figura 6-6: Il valore della riduzione dell’incertezza
Supponiamo che una ragazza con utilità del tipo Von NM
data da U = 1 – 1/M debba scegliere se indirizzare la
propria carriera verso l’insegnamento oppure verso la
recitazione in teatro in condizioni di incertezza. Se decide
di fare l’insegnante M = 5 con certezza. Se decide di fare
l’attrice EV = 0,01*(400) + 0,99*(2).
Quale sarà la scelta in condizioni di incertezza?
Utilità attesa opzione 1:
Utilità attesa opzione 2:
EU1 1*U1 1*11/5  0,8
EU2  0,001*U1 0,99*U2 
 0,001*11/400 0,99*11/2  0,505
Una informazione privata sulle probabilità facilita la scelta se
tentare la carriera di attrice.
Possiamo dire quale sarà il “valore” di un’informazione
privata?
P = prezzo massimo che la ragazza sarà disposta a pagare
per avere l’informazione che rimuove l’incertezza
1 
1 


EU3  0,01* 1
0,99* 1
 EU1  0,8
P  0,049
 400 P
 5 P
Figura 6-7: Prospettive di carriera dopo aver frequentato l’università A o
B
Con una funzione di utilità U=√M si sceglie
università B anche se il valore atteso è minore
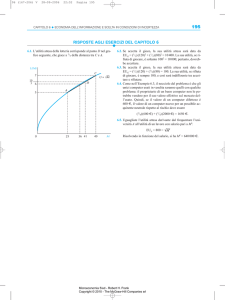
Figura 6-8: Livelli di utilità attesa dalle alternative di scelta delle
università
ES: 6.5 Il certo equivalente di una scommessa è la somma certa
che fornisce la stessa utilità della scommessa. Nel caso di questo
gioco se VA=700.000; UA=800 il C.E. = UA=√X= 800 
X=8002=640.000 euro
RISCHIO E ASSICURAZIONI
 Quando i rischi che differenti soggetti si trovano ad
affrontare sono indipendenti, agendo collettivamente è
possibile ottenere un risultato preferito da tutti
 Alla base della condivisione dei rischi risiede la legge
dei grandi numeri: quando un evento incerto è ripetuto
un numero sufficiente di volte le occorrenze tendono a
convergere alle probabilità
 Le società di capitale hanno lo scopo di ridurre il rischio
per il singolo investitore
 Il mercato delle assicurazioni fornisce l’esempio tipico
di riduzione del rischio
RISCHIO E ASSICURAZIONI
Dal punto di vista del singolo consumatore,
tuttavia, l’acquisto di un’assicurazione è un
gioco non equo in quanto le compagnie di
assicurazione devono far fronte ai propri costi
Ci sono limiti alla traslazione del rischio ad altri
soggetti: il cosiddetto rischio morale connesso
al fatto che esiste un incentivo, da parte degli
assicurati, a comportarsi in maniera negligente o
persino fraudolenta - ciò aumenta ancora i costi
di assicurazione
Figura 6-9: Il prezzo di riserva per l’assicurazione
Questo individuo ha
1/3 di probabilità di
perdere 600 (rispetto
ad una ricchezza
iniziale di 700)
EC VA
Figura A6-1: Ipotetica distribuzione uniforme delle retribuzioni
Dove si deve fermare la ricerca (razionale) di un
lavoro meglio retribuito?
Figura A6-2: Valore atteso di un’offerta maggiore di 150 €
La probabilità è equidistribuita tra 100 e 200. Se
vi offrono 150 ed il costo di ricerca ulteriore è 5,
dovete fermarvi o continuare? Il guadagno atteso
(neutralità al rischio assunta) è 0,5*(175150)=12,5
Figura A6-3: Retribuzione accettabile
Il guadagno atteso da una ricerca ulteriore è sempre (200w)/2 e la probabilità (200-w)/100. Da cui la ricerca
converrà sintanto che w è tale che (200-w)2/200>5
200 w 200 w  200 w 
EGw
   100  2  200  5
*
*
* 2
*
w 200 w  1000w*  200 1000168,38
*
* 2