La seconda prova scritta dell`esame di stato 2007

La seconda prova scritta dell’esame di stato 2007
Indirizzo: GEOMETRI
Tema di TOPOGRAFIA
Claudio Pigato
Istituto Tecnico Statale per Geometri “Bernini” – Rovigo – E-mail: [email protected]
1. Determinazione delle coordinate dei vertici dell’appezzamento
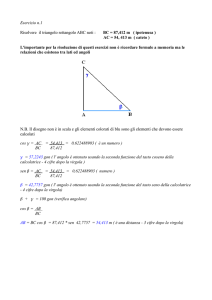
Si comincia con la risoluzione del triangolo BCD, del quale si conoscono due lati e l’angolo compreso1:
2
2
BD = BC + CD − 2 ⋅ BC ⋅ CD ⋅ cos BCD = 511,788 m
2
2
2
BD + CD − BC
BDC = arccos
= 47,7562 gon
2 ⋅ BD ⋅ CD
DBC = 200 – (BDC + BCD) = 66,9223 gon
Per risolvere il quadrilatero ABDE si conoscono ora tre lati e i due angoli non compresi, per cui conviene
mandare da B e D le perpendicolari ad AE fino ai punti K e H, e da D la perpendicolare al lato BK (vedi
figura 1).
Triangolo rettangolo EHD:
Triangolo rettangolo AKB:
Triangolo rettangolo BLD:
EH = ED ⋅ cos AED = 301,652 m
HD = ED ⋅ sen AED = 392,970 m
AK = AB ⋅ cos EAB = 63,413 m
KB = AB ⋅ sen EAB = 523,494 m
LB = KB - HD = 130,525 m
2
2
LD = BD − LB = 494,864m
KBD = arccos
LB
= 83,5825 gon
BD
EA = AK + LD + HE = 859,929 m
Passiamo ora al triangolo GFE, di cui si conoscono 2 lati ed un angolo (si noti che, essendo l’angolo noto
ottuso, si può in questo caso applicare il teorema dei seni per determinare gli altri angoli incogniti):
2
2
GE = GF + EF − 2 ⋅ GF ⋅ EF ⋅ cos GFE = 878,445 m
FEG = arcsen
FG ⋅ sen GFE
= 39,2826 gon
GE
Infine, consideriamo il triangolo GEA, del quale sono noti i tre lati:
1
Si trascura l’orientamento nell’indicazione degli angoli, non essendo stata considerata nel testo.
2
2
2
EG + EA − AG
GEA = arccos
= 55,0361 gon
2 ⋅ EG ⋅ EA
Fig. 1
2
2
2
GA + EA − EG
GAE = arccos
= 73,9514 gon
2 ⋅ GA ⋅ EA
AGE = 200 – (GEA + GAE) = 71,0125 gon
Per calcolare le coordinate dei vertici si calcolano preliminarmente gli azimut:
ϑAB = 200 - EAB = 107,6742 gon
ϑBC = ϑBA - ABC = ϑAB + 200 - ABC = 149,4950 gon
essendo: ABK=arccos
BK
= 7,6744 gon e ABC = ABK + KBD + DBC = 158,1792 gon
AB
ϑED = AED = 58,3215 gon
ϑAG = 200 + GAE = 273,9514 gon
ϑEF = 400 − GEA - FEG = 305,6813 gon
Le coordinate planimetriche dei vertici valgono pertanto:
 x B = KB = 523,494 m

 y B = y A - AK = 796,516 m
 xC = x B + BC ⋅ sen ϑBC = 778,920 m

 y C = y B + BC ⋅ cos ϑBC = 545,109 m
 x D = HD = 392,970 m

 y D = EH = 301,652 m
 x F = EF ⋅ sen ϑEF = −400,926 m

 y F = EF ⋅ cos ϑEF = 35,875 m
 xG = AG ⋅ sen ϑAG = −668,298 m

 yG = y A + AG ⋅ cos ϑAG = 570,125 m
2. Frazionamento dell’appezzamento AEFGA
Essendo note le coordinate dei vertici, è conveniente applicare la formula di Gauss per determinare l’area:
A = A(ABCDEA) =
1
[x B ⋅ ( y A − yC ) + xC ⋅ ( y B − y D ) + x D ⋅ yC ] = 382.238,3 m 2
2
Le aree delle tre superfici derivate sono pertanto:
A1 = A / 6 = 63.706,4 m2
A2 = 2 A1 = 127.412,8 m2
A3 = 3 A1 = 191.119,2 m2
Si applica ora il problema del trapezio per le due nuove dividenti, verificando però che la loro posizione sia
contenuta all’interno dei lati ED e AB:
MN = AE − 2 ⋅ A1 ⋅ (cot EAB + cot AED ) = 791,353 m
2
L’altezza del primo trapezio e le lunghezze degli estremi della nuova dividente dai vertici A ed E sono:
h1 =
h1
h1
2 ⋅ A1
= 77,160 m ; EM =
= 97,272 m ; AN =
= 77,724 m
sen AED
sen EAB
AE + MN
Per determinare la seconda dividente, è sufficiente ripetere il procedimento sopra indicato, considerando il
trapezio AQPE, la cui area A1+A2 è uguale ad A3:
PQ = AE − 2 ⋅ A 3 ⋅ (cot EAB + cot AED ) = 632,267 m
2
h2 =
2 ⋅ A3
h2
h2
= 256,158 m ; EP =
= 322,926 m < ED ; AQ =
= 258,030 m < AB
sen AED
sen EAB
AE + PQ
3. Spianamento dell’appezzamento AEFGA
Per determinare la quota di progetto, calcoliamo il volume fittizio di terreno delimitato dalle due falde AEG
e EFG ed un piano di riferimento assunto a quota 590 m:
Vf = A(AGE) ⋅
11,454 + 29,327 + 0,328
0,328 + 29,327 + 15,327
+ A(GFE) ⋅
= 5.471.392 m 3
3
3
essendo le aree delle due falde pari a:
A(AGE) =
1
1
y A ⋅ xG = 287.344,4 m 2 ; A(EFG) = FG ⋅ FE ⋅ sen GFE = 102.301,7 m 2
2
2
L’altezza di progetto h si determina quindi dividendo il volume fittizio per l’area dell’appezzamento,
ipotizzando nullo l’aumento di volume di scavo.
h=
Vf
= 14,042 m ; q = 590 + h = 604,042 m
A(AEFG)
Eseguendo la differenza tra quota di progetto e quote del terreno si determinano le quote rosse:
rA = q – QA = 2,588 m ;
rE = q – QE = -15,285 m
rF = q – QF = -1,285 m ;
rG = q – QG = 13,714 m
I punti di passaggio R, S e T si trovano in corrispondenza dei lati con alternanza di segno nelle quote rosse:
ER = EA ⋅
rE
= 735,411 m
rE + rA
ES = EG ⋅
rE
= 463,017 m
rE + rG
FT = FG ⋅
rF
rF + rG
= 51,183 m
Per calcolare il volume di sterro si dovrà suddividere la falda ESTF in due triangoli (è indifferente una
diagonale oppure l’altra), calcolandone l’area:
2
2
ET = EF + FT − 2 ⋅ EF ⋅ FT ⋅ cos GFE = 431,625 m
TEF = arcsen
FT ⋅ sen GFE
= 6,4339 gon
ET
TES = FEG – TEF = 32,8487 gon
1
FE ⋅ ET ⋅ sen TEF = 8.764,5 m 2
2
1
A(TES) = ES ⋅ ET ⋅ sen TES = 49.302,2 m 2
2
1
A(ESR) = ES ⋅ ER ⋅ sen GEA = 129.524,8 m 2
2
A(FET) =
Possiamo finalmente calcolare il volume di sterro, che naturalmente corrisponderà al volume di riporto,
trattandosi di spianamento di compenso:
Vst = A(FET) ⋅
rF + rE
r
r
+ A(TES) ⋅ E + A(ESR) ⋅ E = 959.533 m 3
3
3
3
4. Piano di volo aerofotogrammetrico
Determiniamo anzitutto la scala media del fotogramma, che può essere orientativamente fornita dalla
seguente formula empirica:
n f = 200 nc = 200 500 ≅ 4.500
Assumiamo pertanto per scala media dei fotogrammi il valore 1:4.500. La quota media di volo risulta quindi,
dato che la distanza principale p della fotocamera è nota:
q = 4.500 × p = 4.500 × 0,153 = 688,5 m
La velocità massima del velivolo può essere determinata considerando il trascinamento ammesso τ di 0,03
mm:
v max ⋅ t E = τ ⋅ n f
⇒ v max =
τ ⋅nf
0,03 4.500
=
⋅
= 135 m/s = 486 km/h
1.000 1 / 1.000
tE
La larghezza di ripresa e la distanza tra una ripresa e la successiva valgono:
L = ⋅ n f = 1.035 m
; b = (1 - ηl ) ⋅ L = 414 m
Assumendo quindi una velocità di 450 km/h, l’intervallo di scatto tra un fotogramma ed il successivo vale:
∆t =
414
b
=
= 3,3 s
v 450 / 3,6
Per determinare il numero di fotogrammi per effettuare una strisciata, osserviamo che la distanza massima
lungo x dell’appezzamento vale xC – xG = 1.447 m. Indicato con n il numero di fotogrammi per strisciata, si
ha la seguente equazione che fornisce la lunghezza di ricoprimento stereoscopico:
Lx = ηl × L + (n-2) b
n = (1.447-621)/414 + 2 = 4,00 5
Pur essendo sufficienti 4 fotogrammi per strisciata, si ritiene cautelativo eseguirne 5.
Un’unica strisciata è sufficiente a rilevare la larghezza dell’appezzamento, pari a yA.
Il numero totale dei fotogrammi necessari è pertanto pari a 5×1 = 5 (fig. 2).
Fig. 2