RISOLUZIONE VERIFICA 3ACAT del 7 dicembre 2016
esercizio 1
dati
A
B
x
y
-152,245
14,568
47,568
-10,557
calcolo AB utilizzando la formula per il calcolo della distanza tra due ponti
AB=
176,650 m
calcolo l'azimut con l'arctan
q= 121,3451
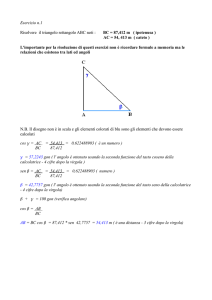
esercizio 2
dati
A
B
C
x
y
56,342
126,842
85,337
12,31
68,472
-21,753
risolvere il triangolo ABC
calcolo i lati con la formula della distanza tra due punti
AB=
90,136 m
BC=
99,314 m
CA=
44,733 m
a questo punto posso calcolare il perimetro
2p= 234,182 m
e l'area con la formula di erone (semiperimetro)
2
area=
2015 m
per il calcolo degli angoli posso utilizzare gli azimut oppure la formula inversa del coseno
a= 97,9296 gon
b= 29,7279 gon
g= 200-a-b=
72,3425 gon
esrcizio 3
di un quadrilatero ABCD sono noti:
AB= 121,123 m
BC= 168,315 m
CD= 134,235 m
b= 112,765 go
g= 122,509 gon
risolvere il quadrilatero
posso calcolare immediatamente l'area con la formula di camminamento
conoscendo tre lati e i due angoli compresi
2
area=
24865 m
proseguo poi scomponendo il quadrilatero nei due triangoli ABC eACD
triangolo ABC
calcolo AC utilizzando il teorema di Carnot
AC= 226,101 m
quindi calcolo a1
con la formula inversa del seno
a1=
52,050 gon
per differenza calcolo l'angolo g1 =
35,185 gon
triangolo ACD
calcolo l'angolo g2=g-g1 =
87,324 gon
quindi calcolo il lato AD utilizzando Carnot
AD= 239,028 m
quindi calcolo a2
con la formula inversa del seno
a2=
37,112
quindi a=a1+a2=
89,162 gon
e l'angolo d è ricavabile per differenza ricordando che la somma degli angoli del quadrilatero è 400 gon
d=
75,564 gon
da ultimo il perimetro
2p= 662,701 m