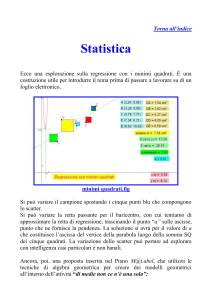
Un’introduzione
L’integrazione numerica sviluppa metodi
che, basandosi su importanti risultati
dell’Analisi Matematica, consentono una
valutazione APPROSSIMATA di integrali
definiti
∫
b
a
f ( x ) dx
Quando non è possibile determinare una
primitiva di f(x) mediante
funzioni elementari
sin
x
(es. f(x)=e − x
, f(x)= x )
Quando la determinazione di una primitiva di
f(x) è particolarmente laboriosa
Quando la funzione integranda è una funzione
empirica, cioè una funzione di cui sono noti
solo dei valori tabulati (dati sperimentali)
2
…approssimando f(x) con una funzione COSTANTE
A TRATTI (funzione razionale intera di grado
zero)…
y
O
f(x)
x
Vogliamo calcolare un valore approssimato J di
b
I = ∫ f ( x)dx
a
b−a
h=
n
x0=a, x1=a+h, x2=a+2h, …, xn=a+nh=b
y0=f(x0), y1=f(x1), …, yn-1=f(xn-1)
Formula dei rettangoli
f(x)
y
{
{
y4
y0
●
a=x0
●
x1
{
O
passo d’integrazione
●
x2
●
x3
●
x4
●
x5=b
h
J = h ( y 0 + y 1 + ... + y n − 1 )
x
…approssimando f(x) con una funzione LINEARE
A TRATTI (funzione razionale intera di grado
uno)…
y
O
f(x)
x
y 0 + y1
y n −1 + y n
y1 + y 2
,h
,..., h
h
2
2
2
Aree dei trapezi:
Somma aree trapezi
b−a
h=
n
h
[( y 0 + y1 ) + ( y1 + y 2 ) + ... + ( y n −1 + y n ) ]
2
y
f(x)
Formula dei trapezi
o di Bezout
O
●
●
a=x0 x1
●
x2
●
x3
●
x4
●
x5=b
h
J = ( y 0 + 2 y 1 + 2 y 2 + ... + 2 y n −1 + y n )
2
x
…approssimando f(x) con PARABOLE (funzioni
razionali intere di grado due)…
b−a
h=
n
x0 = a, x1 = x0 + h, x2 = x0 + 2h
y0 = f ( x0 ), y1 = f ( x1 ), y2 = f ( x2 )
y = Ax 2 + Bx + C
Impongo che la parabola
passi per
( x0 , y0 ), ( x1 , y1 ), ( x2 , y2 )
trovo A,B,C
P( x0 , y0 ), Q( x1 , y1 ), R( x2 , y2 )
x2
x2
h
2
∫x0 ( Ax + Bx + C)dx = 3 ( y0 + 4 y1 + y2 ) ≅ ∫x0 f ( x)dx
Q
P
NOTA BENE
R
Suddivido [a,b]
in un numero
PARI di intervalli
Analogamente si trova che
∫
f ( x)dx ≅
h
( y 2 + 4 y3 + y 4 )
3
f ( x)dx ≅
h
( y 4 + 4 y5 + y 6 )
3
x4
x2
∫
x6
x4
∫
.......................
xn
xn−2
f ( x)dx ≅
∫
Poichè
segue
h
( yn − 2 + 4 yn −1 + yn )
3
x2
x0
x4
xn
x2
xn−2
f (x)dx + ∫ f (x)dx + ...+ ∫
b
f (x)dx = ∫ f (x)dx
a
h
[(y0 +4y1 + y2)+(y2 +4y3 + y4)+...+(yn−2 +4yn−1 + yn)]
f
(
x
)
dx
≅
∫a
3
b
Formula di
CavalieriSimpson
h
J = (y0 +4y1 +2y2 +4y3 +2y4 +...+2yn−2 +4yn−1 +yn)
3
Dimostrazione di Cavalieri-Simpson
•
•
•
1.
2.
I metodi di integrazione numerica sono metodi
approssimati. E’ dunque importante saper valutare
l’errore che si commette utilizzando tali metodi.
Una prima fonte di errori è causata dagli
arrotondamenti che si operano nei calcoli.
Per evitare tali errori di arrotondamento è bene
adottare i seguenti accorgimenti:
si scelga un passo d’integrazione h il cui valore sia
dotato di un numero finito di cifre decimali. In questo
modo i valori di x1, x2, … non saranno affetti da errori;
si eseguano calcoli con un numero di cifre decimali
doppio rispetto a quelle che si desiderano esatte nel
risultato: in tal modo difficilmente l’accumularsi degli
errori di arrotondamento potrà influire sulle cifre
decimali che si desidera conoscere.
• In ogni caso, anche se con gli
accorgimenti enunciati si riesce a ridurre la
portata degli errori di arrotondamento,
resta il fatto che i metodi di integrazione
numerica sono metodi approssimati e i
risultati da essi forniti sono affetti da errori
di metodo, che non dipendono
dall’accuratezza del calcolo.
• Per valutare l’errore di metodo commesso,
si può ricorrere al…
• Supponiamo di dover calcolare l’integrale
b
I =
∫
f ( x ) dx .
a
• Applicando uno dei metodi esposti con un passo di
integrazione h, otteniamo un’approssimazione J1 affetta
da un errore e1=J1-I.
• Applichiamo nuovamente lo stesso metodo, ma con un
passo di integrazione h/2, pari alla metà di quello
utilizzato prima.
• Otteniamo un’approssimazione J2 affetta da un errore
e2=J2-I.
• Procedendo in tal modo si può dimostrare che per
ciascun metodo si può ottenere un’approssimazione
dell’errore commesso che indicheremo con ε e che
riportiamo nella seguente tabella riassuntiva:
Metodo
Formula
Errore
Rettangoli
J=h(y0+y1+…+yn)
ε =| J 1 − J 2 |
J=h/2(y0+2y1+…+2yn-1+yn)
| J1 − J 2 |
ε=
3
J=h/3(y0+4y1+2y2+…+2yn-2+4yn-1+yn)
(n pari)
| J1 − J 2 |
ε=
15
Trapezi
CavalieriSimpson
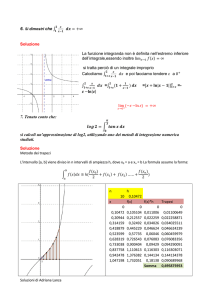
Esempio di valutazione dell’errore
1
•
•
•
•
•
•
•
1
dx
x2 + 1
Vogliamo calcolare l’integrale −∫1
Usiamo la formula di Cavalieri-Simpson.
Suddividiamo l’intervallo [-1,1] in 2 parti: h=1.
Otteniamo J 1 = 5 ≅ 1 . 6666 ....
3
Dimezziamo il passo di integrazione: h=0.5
Otteniamo J 2 = 47 ≅ 1 . 5666 ....
30
L’errore è
| 47 − 5 |
1
ε ≅
30
15
3 =
150
≅ 0 .00666 ...
• Dunque concludiamo che
1
1
∫−1 x 2 + 1 dx = 1.5666.... ± 0.006666....
1
1
→ 1.56 ≤ ∫ 2
dx ≤ 1.573333...
x +1
−1