6. Si dimostri che
Soluzione
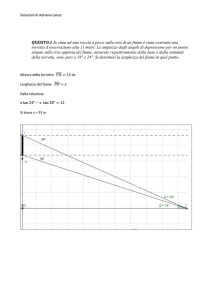
La funzione integranda non è definita nell’estremo inferiore
dell’integrale,essendo inoltre
si tratta perciò di un integrale improprio
Calcoliamo
e poi facciamo tendere
=
a
=
=-
7. Tenuto conto che:
si calcoli un'approssimazione di log2, utilizzando uno dei metodi di integrazione numerica
studiati.
Soluzione
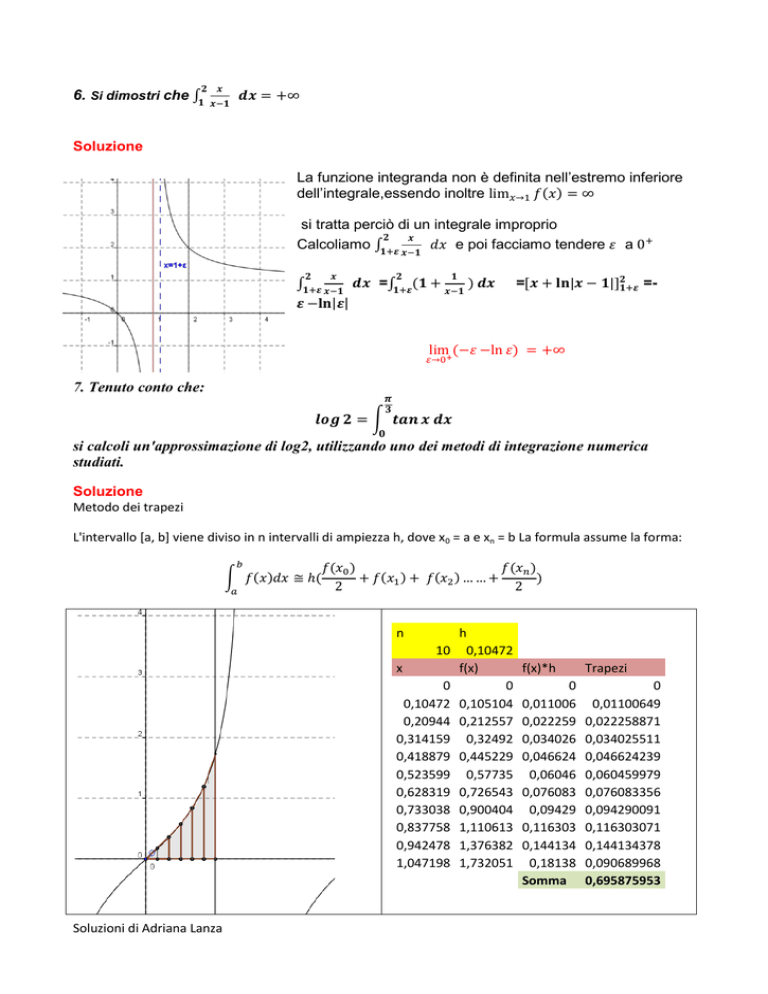
Metodo dei trapezi
L'intervallo [a, b] viene diviso in n intervalli di ampiezza h, dove x0 = a e xn = b La formula assume la forma:
n
10
x
0
0,10472
0,20944
0,314159
0,418879
0,523599
0,628319
0,733038
0,837758
0,942478
1,047198
Soluzioni di Adriana Lanza
h
0,10472
f(x)
0
0,105104
0,212557
0,32492
0,445229
0,57735
0,726543
0,900404
1,110613
1,376382
1,732051
f(x)*h
Trapezi
0
0,011006
0,022259
0,034026
0,046624
0,06046
0,076083
0,09429
0,116303
0,144134
0,18138
Somma
0
0,01100649
0,022258871
0,034025511
0,046624239
0,060459979
0,076083356
0,094290091
0,116303071
0,144134378
0,090689968
0,695875953
8.Si determini per quale valore di x si ha
Soluzione
Passando ai logaritmi di ciascuno dei due membri
9.Si determini la probabilità che in otto lanci di una moneta si presenti croce un numero dispari di
volte.
Soluzione
Distribuzione binomiale : la probabilità che su 8 lanci esca k volte croce è
Probabilità che esca un numero dispari
Probabilità che esca un numero pari
(
(
Poiché la somma dei coefficienti binomiali di posto dispari è uguale alla somma dei coefficienti binomiali
di posto pari ( come si può anche verificare direttamente) ed uguale , in questo caso,a
=
le due probabilità sono uguali tra loro ( come suggerisce l’intuizione) ed uguali a
10. In una figliata di quattro gattini, è più probabile che due siano maschi e due siano femmine,
oppure che tre siano di un sesso e uno dell'altro
Soluzione
MMFF
probabilità uguale a
=
M FFF MMMF probabilità uguale a
La seconda probabilità è maggiore della prima
Soluzioni di Adriana Lanza