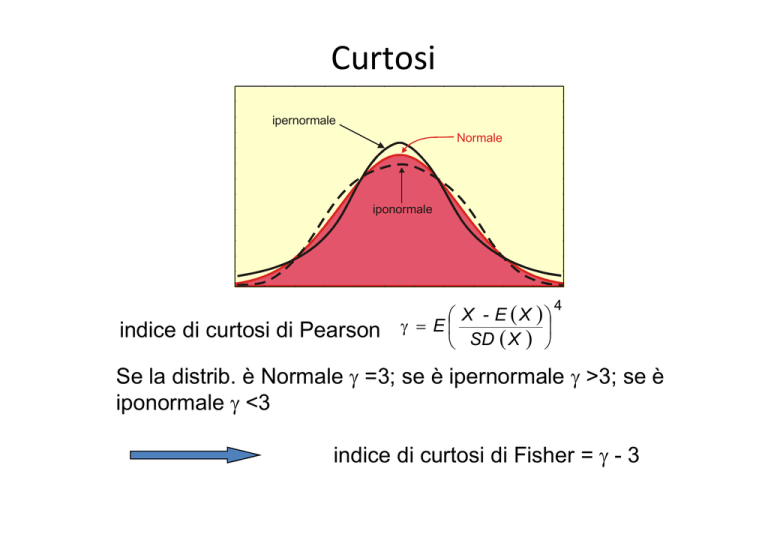
Curtosi
ipernormale
Normale
iponormale
indice di curtosi di Pearson
X - E (X )
γ = E
(
)
SD
X
4
Se la distrib. è Normale γ =3; se è ipernormale γ >3; se è
iponormale γ <3
indice di curtosi di Fisher = γ - 3
Distribuzione Chi-quadrato
La v.c. Chi-quadrato è una distribuzione
asimmetrica, continua e definita per valori reali non
negativi. La funzione di densità dipende da un unico
parametro, chiamato gradi di libertà, che è un intero
positivo che possiamo indicare con il simbolo g.
f (x ) =
E (X ) = g
g
x
−1 −
x2 e 2
1
g
22
g
Γ
2
V ( X ) = 2g
per x ≥ 0
Distribuzione Chi-quadrato
χ 2 (4 )
0,15
χ 2 (8)
χ 2 (12)
0,10
χ 2 (20 )
0,05
0,00
0,0
7,5
15,0
22,5
30,0
All’aumentare di g la distribuzione tende ad una Normale.
Si può ottenere come somma di g v.c. Normali
Standardizzate al quadrato
ALTRE DISTRIBUZIONI
•t di Student :
T ≈ Student ( g ) (o v.c. t )
“somiglia alla normale standardizzata”; è continua e definita
su tutto l’asse reale; dipende da un solo parametro g, che è
un intero positivo; all’aumentare di questo tende alla N(0,1)
(approssimazione buona già per g>30)
Da ricordare:
Sia
Z ≈ N (0,1) e sia χ ≈ χ ( g ) allora la v.c.
2
X=
Z
χ
2
g
2
≈ t di Student con g g.d.l.
•F di Fisher:
F ≈ Fisher (ν 1 ,ν 2 )
Può assumere valori su tutto l’asse reale e dipende da
due parametri interi positivi
Da ricordare
Sia :
χ ≈ χ (g1) e sia χ ≈ χ (g2 ) allora la v.c.
2
1
2
2
2
χ
2
1
X=
χ
2
2
g1
g2
≈ F(g1, g2 )
2
Teorema del limite centrale
Motiva ulteriormente il ruolo della Normale in statistica: molti fenomeni infatti
possono essere interpretati come la media o la somma di un elevato n° di v.c.
indipendenti.
Attraverso tale teorema si dimostra che la distribuzione della media o della somma
di n v.c. indipendenti tende alla distribuzione di una v.c. normale quando n diventa
infinitamente grande.
Teorema del limite centrale
Sia X1, X2, X3,… una successione di variabili casuali indipendenti e identicamente
distribuite (iid), con media μ e varianza σ2 finite, posto
1
Xn =
n
n
∑X
i
i =1
si ha che la v.c.
Zn =
( X n − µ)
n
σ
converge in distribuzione, per n → ∞, alla v.c. Normale standardizzata
esempio
esempio
Il risultato è rilevante :
a) Non si assume alcuna ipotesi sulla distribuzione delle v.c. di
partenza, le quali possono essere sia discrete che continue ed
avere una distribuzione molto diversa da quella normale.
b) Ogni volta che una v.c. può essere espressa come media di
v.c. indipendenti con stesso v. atteso e stessa varianza per n
sufficientemente grande è possibile approssimare la
probabilità che essa assume valori in un dato intervallo (a,b)
utilizzando la f.d.r. di una normale standardizzata; infatti:
X
−
µ
a
−
µ
b
−
µ
P ( a ≤ X n ≤ b ) = P
≤ n
≤
σ
σ
σ
n
n
n
a
−
b
−
µ
µ
= P
≤ Zn ≤
σ
σ
n
n
dove Z n è una Z ≈ N (0,1)
c) Il teorema del limite centrale può anche
essere applicato alla somma di v.c.
indipendenti; se indichiamo con:
n
Yn = ∑ X i allora E (Yn ) = nµ ; Var(Yn ) = nσ 2
i =1
e poichè Yn = nX n si avrà:
Yn − E (Yn )
Var (Yn )
=
nX n − n µ
nσ
2
=
Xn − µ
σ /n
2
= Z n = Z ≈ N (0,1)
Applicazioni del teorema
La v.c. Binomiale può essere vista come la somma di n prove Bernoulliane
indipendenti (cioè n v. casuali iid): dato un n sufficientemente grande la sua
distribuzione è molto simile ad una variabile casuale Normale con v. atteso
nπ e varianza nπ(1 – π)
Consideriamo una successione di Poisson del tipo X1 ∼ P(λ1), X2 ∼ P(λ1 + λ2),
X3 ∼ P(λ1 + λ2 + λ3), ... con λi > 0: se λ1 = λ2 = λ3 = … si ha che la distribuzione
Xn può essere approssimata, per n grande, da una v. casuale Normale con
valore atteso nλ e varianza nλ
X ∼ N (nπ, nπ(1 – π))
X ∼ N (nλ, nλ)
0,40
Poisson(1)
0,35
0,30
0,25
0,20
Poisson(7)
0,15
0,10
0,05
0,00
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Alcuni accorgimenti per l’approssimazione
In alcuni casi, nonostante l’apparente contraddizione, è possibile approssimare
le distribuzioni di probabilità discrete alla distribuzione normale: occorre però
tenere conto che i valori possibili delle discrete sono assimilabili ad un insieme
di numeri interi naturali (0, ..., n, ...) mentre per la Gaussiana si ha che x∈
∈R
Per superare tali problemi si usa un fattore di correzione della continuità
pari a 0,5 : se X è una v. discreta ed è approssimata con una v. continua Y
P(a < X < b) = P(a + 0,5 ≤ Y ≤ b - 0,5)
a
b
P(a ≤ X ≤ b) = P(a - 0,5 ≤ Y ≤ b + 0,5)
a
b
Se gli estremi sono esclusi si
restringe l’intervallo ]a;b[
Se gli estremi sono inclusi si
allarga l’intervallo [a;b]
Approssimazione della Binomiale
La Normale è una buona approssimazione della Binomiale se:
n, il numero delle prove, è molto grande
π, la probabilità di successo, è molto vicino a 0.5
π
π
π
π
π
π
π
π
Come si vede, all'aumentare di n la distribuzione assume una forma sempre
più campanulare giustificando l'uso di una distribuzione normale
Per calcolare la probabilità che la X assuma valori in un certo intervallo, una
volta calcolati il valore atteso e la varianza, si utilizzano le tavole della v. cas.
Normale
Esempio
Le nuove imprese hanno il 50% di probabilità di fallire
nel loro primo anno di attività. Qual è la probabilità che
in un campione di 100 imprese commerciali 40 siano
ancora in attività dopo il primo esercizio?
100
100!
40
60
40
60
P(X=40) =
0,5
0,5
=
⋅
0,5
0,5
= 0,0108
40!60!
40
Proviamo a calcolare la probabilità utilizzando l’approssimazione alla normale
μ = nπ = 100⋅0,5 = 50
σ2 = nπ(1 – π) = 25
PERCHE’??
P(X = 40) ≅ P(39,5 ≤ Y ≤ 40,5) =
= P(-2,1 ≤ Z ≤ -1,9) → P(1,9 ≤ Z ≤ 2,1) = φ(2,1) - φ(1,9) =
= 0,9821 - 0,9713 = 0,0108
Esercizio (1)
Il 20% degli individui è convinto di sopravvivere ad un
incidente aereo. Si indichi con Y il n° di tali persone in
un campione di ampiezza n=25. Qual è la probabilità
che il numero di individui convinti di sopravvivere sia
compreso tra 6 e 9?
μ = nπ = 25⋅0,2 = 5
σ2 = nπ(1 – π) = 4
6
25
25
i
25-i
P(6 ≤ X ≤ 9) = ∑ 0,2 0,8 - ∑ 0,2 i 0,8 25-i =0,3659
i=0 i
i=0 i
9
Per approssimazione
5,5 - 5 Y - 5 9,5 - 5
P(6 ≤ X ≤ 9) = P(5,5 ≤ Y ≤ 9,5) =P
≤
≤
=
2
2
2
= P(0,25 ≤ Z ≤ 2,25) = φ(2,25) - φ(0,25) = 0,3891
Perché???
Esercizio (2)
L'asimmetria della binomiale (dovuta a π lontano da 0,5) ha comportato una
notevole differenza nell'approssimazione della probabilità
Approssimazione della Poisson
La distribuzione Poissoniana è approssimabile alla distribuzione normale con
μ = λ e σ2 = λ, sotto la condizione che il valore medio sia almeno pari a 10
Esempio
Il n° di vendite settimanali di un certo prodotto segue la legge Poissoniana con
una media di 2 vendite al giorno. Qual è la probabilità che in una settimana si
vendano al più 23 prodotti?
Se consideriamo una media di 2 vendite al giorno avremo 14 prodotti in una
settimana, per cui
P ( X ≤ 23 ) =
23
∑
k=0
14 k e -14
= 0,9907
k!
Approssimando la distribuzione alla Normale otteniamo
0 - 0,5 - 14
23
+
0,5
-14
P(0 ≤ X ≤ 23) = P
≤Z≤
=
3,7417
3,7417
= P(-3,88 ≤ Z ≤ 2,54) = φ(2,54) - [1- φ(3,88)] = 0,9944
Variabile aleatoria proporzione
In molti problemi applicativi occorre calcolare probabilità
associate a frequenze relative e a percentuali. A tal fine si utilizza
una estensione diretta della approssimazione normale alla
distribuzione binomiale. La v.c. proporzione P può essere
ottenuta dividendo il n° di successi X per la dimensione del
campione n :
X
P=
n
Ed usando la trasformazione lineare di v.c., si avrà
µ=p
p(1− p)
2
σ =
n
Esempio: proiezioni elettorali
Consideriamo un campione relativamente piccolo per fare
previsioni elettorali.
Un incaricato di una società demoscopica ha usato un campione
casuale di 900 elettori dei quali 500 dichiarano che voteranno
per il candidato Tizio. Tizio dovrà diffondere in anticipo la
notizia?
SOLUZIONE
In questo problema si ipotizza che vi sono solo due candidati e
quindi se più del 50% della Popolazione lo voterà, Tizio avrà vinto
le elezioni. Calcoliamo la probabilità che almeno 500 elettori del
campione votino Tizio, nell’ipotesi che esattamente il 50% della
popolazione voti a suo favore (p=0.50).
Sarà:
P( X ≥ 500/n = 900, p = 0.50) P( X ≥ 500/µ = 450,σ 2 = 225)
500 − 450
= P(Z ≥
) = P(Z ≥ 3.33) = 0.00
225
La probabilità di 500 successi su 900 prove, quando p=0.50 è
molto piccola e perciò p deve essere maggiore di 0.50 e quindi
Tizio vincerà le elezioni.
Possiamo anche calcolare la probabilità che più del 55.6%
(500/900) del campione indichi la preferenza per Tizio nel caso in
cui la proporzione nella popolazione sia p=0.50. Usando media e
varianza della proporzione
Sarà:
µ
σ
σ
=
= 0 .5 0
0 . 5 0 (1 − 0 . 5 0 )
2
=
9 0 0
= 0 .0 1 6 7
p
E:
P(P ≥ 0.556/n = 900, p = 0.50) P(P ≥ 0.556/µ = 0.50,σ = 0.0167)
0.556 − 0.50
= P(Z ≥
) = P(Z ≥ 3.33) = 0.00
0.0167
La probabilità è la stessa perché ogni proporzione o valore percentuale è
direttamente legato ad uno specifico numero di successi.
Un’applicazione della Normale: la media campionaria
Supponiamo di voler estrarre da una popolazione un campione casuale e di
osservare su questo il fenomeno oggetto d’interesse: ad esempio vogliamo
intervistare alcuni consumatori per valutare il loro livello di spesa in prodotti
di largo consumo
Gli n soggetti che compongono il campione casuale rappresentano di fatto
un insieme di n variabili casuali
X1 , X 2 ,K , X n
Ogni v.c. è indipendente e ha uguale distribuzione di probabilità
Possiamo considerare congiuntamente tutta l’informazione espressa dalle
diverse osservazioni campionarie per mezzo di particolari funzioni chiamate
statistiche : essendo funzione di più variabili casuali ogni statistica è a sua
volta una variabile casuale, con una sua distribuzione di probabilità
1 n
X = ∑ Xi
n i =1
la media campionaria è una statistica che
consente di esprimere sinteticamente in
un unico valore l’informazione contenuta
in tutti i possibili campioni
Esempio
Consideriamo una popolazione finita composta dalle seguenti 5 unità:
x1 = 8 x2 = 4 x3 = 2 x4 = 11 x5 = 6
Si consideri l’estrazione senza ripetizione di campioni di dimensione n=2 e
per ognuno di essi si calcoli la statistica media campionaria.
X 1 8 8 8 8 4 4 4 4 2 2 2 2 11 11 11 11 6 6 6 6
X2
4 2 11 6 8 2 11 6 8 4 11 6 8
X
6 5 9,5 7 6 3 7,5 5 5 3 6,5 4 9,5 7,5 6,5 8,5 7 5 4 8,5
4
2
6 8 4 2 11
Ogni campione ha probabilità 0,5 di essere estratto e quindi la distribuzione
di probabilità della media campionaria è data da:
X
( )
P X
3
4
5
6
6,5
7
7,5 8,5 9,5
0,1 0,1 0,2 0,1 0,1 0,1 0,1 0,1 0,1
Proprietà
E( X ) = µ
il valore atteso
Var ( X ) = σ
la varianza
Se
X ~ Be(π )
Se
X ~ N µ;σ
(
2
)
allora
allora
2
n
X∼
1
Bin(n,π )
n
σ2
X ~ N µ;
n
Qualunque sia la popolazione, per il Teorema del Limite Centrale
X − µ
lim P
≤ z = P (Z ≤ z )
n→∞ σ n
dove Z è una v.c. Normale standardizzata
Approfondiremo nella seguente lezione i concetti di campione casuale e
di distribuzione della media campionaria