Esercitazione – 05 maggio 2016
ESERCIZIO 1
Una società di servizi possiede un parco auto di diverse età. I dirigenti ritengono che il costo degli
interventi di manutenzione per le auto più vecchie sia generalmente più elevato rispetto a quello per
le auto più nuove. La tabella seguente riporta i dati relativi alle auto utilizzate dalla società:
Età auto (anni)
1 1
2
2
3
3
3
4 4
4
4
5
Costo manutenzione (euro) 253 592 741 722 851 767 1120 1055 959 1625 1600
1379
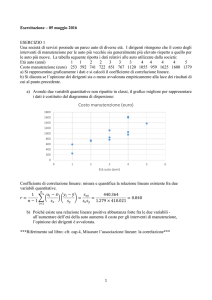
a) Si rappresentino graficamente i dati e si calcoli il coefficiente di correlazione lineare.
b) Si discuta se l’opinione dei dirigenti sia o meno avvalorata empiricamente alla luce dei risultati di
cui al punto precedente.
ESERCIZIO 2
Il consumo giornaliero di acqua potabile (metri cubi) di una famiglia italiana può essere descritto da
una distribuzione normale con media 12 e varianza 9.
a) Calcolare la probabilità che, estraendo un campione casuale di 100 famiglie, il consumo
medio sia superiore a 12.6 metri cubi.
b) Estratta a caso una famiglia, qual è la probabilità che il suo consumo giornaliero di acqua
potabile sia compreso fra 8 e 10 metri cubi?
ESERCIZIO 3
Gli adulti in sovrappeso sono pari al 56% della popolazione italiana fra i 25 e i 64 anni di età.
Estratto a caso un campione di 60 adulti, determinare la probabilità che la proporzione campionaria
di persone in sovrappeso nel campione sia:
a) maggiore di 0.6;
b) minore di 0.4.
ESERCIZIO 4
Su un campione casuale di 220 negozi di libri di una regione italiana, la media settimanale di libri
gialli venduti è risultata pari a 160 con deviazione standard campionaria 46. In una diversa regione
italiana, su un campione casuale di 160 negozi la corrispondente media è risultata pari a 90 con
deviazione standard campionaria 35. Sotto l’ipotesi di normalità del numero di libri gialli venduti
settimanalmente da ciascun negozio, si verifichi al livello 5% l’ipotesi che non vi sia differenza
significativa nelle vendite medie settimanali di libri gialli nelle le due regioni, contro l’ipotesi che il
genere giallo sia più popolare nella prima regione.
ESERCIZIO 5
In un modello di regressione lineare che mette in relazione due grandezze biometriche di un
1 n
campione di 24 soggetti, la covarianza tra x e y,
∑ ( xi − x )( yi − y ) , è pari a 241, la devianza
n − 1 i =1
di x,
n
∑ (x
i
− x ) 2 , è pari a 2506 e la varianza di y è pari 704. Calcolare il coefficiente angolare
i =1
della retta di regressione lineare e la misura sulla bontà dell’adattamento.
ESERCIZIO 6
a) La distribuzione t di Student:
Presenta asimmetria positiva
E’ approssimabile con una normale standardizzata se il numero di gradi di libertà è elevato
Ha media sempre positiva
Non è sempre simmetrica
b) Se in un test a due code sulla media di una variabile X l’ipotesi nulla viene rifiutata per un livello
di significatività pari al 5%, cosa accade aumentando il livello al 10%?
L’ipotesi è rifiutata
L’ipotesi è accettata
Dipende dalla dimensione del campione
E’ necessario calcolare di nuovo la statistica test