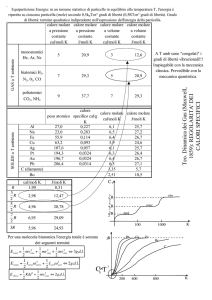
Dipendenza dell'Energia libera dalla T e P
G = H - TS
essendo H = U + PV
G = U + PV - TS
Una variazione infinitesima di una o più variabili che definiscono lo stato del sistema
determina una variazione di G
dG = dU + PdV + VdP - TdS - SdT
Per il I° principio della termodinamica U = Q - L
Per il II° principio della termodinamica dQ = TdS
dU = dQ - dL
dU = TdS - PdV
quindi
dU - TdS + PdV = 0
dG = VdP - SdT
A T costante si ha:
dG = V dP
Questa è la base per dedurre l'espressione dell'energia libera molare di una
qualunque specie chimica ad una determinata temperatura
Miscele di gas ideali
Per una mole di gas ideale si ha: PV = RT
dG = V dP
a T = cost
= energia libera molare standard alla temperatura T
P° è il valore della pressione nelle condizioni standard (1atm)
Per una miscela di gas ideali l'energia libera molare di ciascun componente è:
Nell'argomento del logaritmo compare nominalmente la pressione parziale dell'i-esimo componente
la quale, però, è da intendersi come valore adimensionale perché risultato del rapporto tra pressioni.
Soluzioni ideali ( C< 10-3 F )
Consideriamo una soluzione ideale in equilibrio con il suo vapore (ideale anch'esso)
Per una soluzione ideale è valida la legge di Raoult
Dove Pi° è la pressione di
vapore del componente iesimo allo stato puro
= Energia libera molare standard del componente "i" allo stato puro (infatti xi = 1 ;
Essendoci proporzionalità tra xi , mi , Mi
rappresentano l'energia libera molare standard del soluto
in una soluzione che ha mi o Ci =1
Lo stato standard per un soluto in soluzione è rappresentato da una soluzione
a concentrazione unitaria
Soluzioni reali
Per le soluzioni reali il problema si affronta molto semplicemente
introducendo il concetto di “attività” a = f ·C
Se si fa in modo che il coefficiente di attività sia costante (questo si ottiene
lavorando con una soluzione a forza ionica tamponata, il che significa che nella
soluzione è presente un elettrolita indifferente in grande concentrazione in modo
che le variazioni della concentrazione Ci non provocano la variazione della forza
ionica) allora ci si riporta ad una espressione simile a quella già vista:
Liquidi e solidi puri
dG = V dP
a T = cost
Per i solidi e i liquidi (fasi icomprimibili) il volume è indipendente dalla pressione
In generale il
volume molare di un liquido e/o di un solido è piccolo (per
es. l’acqua ha un volume molare di 0.018 l) quindi se la pressione non è molto
grande si trascura il
(1J = 9.87*10-3 lit*atm)
Esprimendo l’energia libera molare nella forma:
Essendo G = G° per i solidi e i liquidi puri l’attività “a” è unitaria
Miscele di gas reali
Supponiamo, per esempio, di utilizzare come equazione di stato per i gas reali l’equazione
approssimata di Van der Waals che per una mole di gas è:
a $
'
% P + 2 "(V ! b ) = RT
V #
&
Moltiplico e divido l’ultimo membro per P
Ponendo nei due ultimi termini approssimativamente PVҫRT
Essendo (dG)T=VdP
( dG )T = RT
dP
a
ab
+ b dP !
dP + 2 2 P dP
P
RT
RT
Integrando dalla pressione
P=1 alla pressione P
a $
ab
'
2
GT = GTo + RT ln P + % b !
"(P ! 1) + 2 2 P ! 1
RT #
2R T
&
(
)
Miscele di gas reali
Per una mole di gas ideale si ha che PV = RT quindi a T costante
dG = V dP
A questo punto si dovrebbe inserire l’espressione della pressione ricavata dall’equazione
di stato dei gas reali; per semplificare il problema si introduce il concetto di fugacità di
un gas che indica la differenza tra il valore della pressione del gas reale rispetto a quello
che sarebbe se il gas avesse un comportamento ideale
dove γ è la fugacità
Il rapporto adimensionale tra la fugacità nello stato di volta in volta considerato e la
fugacità nello stato standard e designato col nome di attività del gas in quello stato
equivale alla forma:
Se si vuole che la relazione
abbia validità generale
Deve in particolare essere applicabile anche ai gas perfetti per i quali vale la relazione già
vista:
Allora se il gas considerato è un gas perfetto, integrando fra due stati definiti 1 e 2 si trova:
ossia
Dunque per un gas perfetto fugacità e pressione sono fra loro direttamente proporzionali
γ = cost · P
lim
P !0
"
P
=1
Andamento delle concentrazioni delle specie chimiche di una
reazione con il grado di avanzamento.
Reazioni chimiche come processo di avanzamento verso lo stato di equilibrio
Variazione di G nel progressivo avanzamento fino all'equilibrio
aA + bB + cC... → lL + mM + nN...
In cui dni è positivo per i prodotti e
negativo per i reagenti
( dG )T ,P = !G A dnA ! G B dnB !... + G L dnL + G M dnM +...
Le variazioni dei numeri di moli dei diversi componenti dni non sono indipendenti
ma legate alla stechiometria della reazione:
Istante per istante, durante l'avanzamento della reazione, il rapporto fra la
variazione del numero di moli e il coefficiente stechiometrico delle varie specie
chimiche è per tutti uguale
νi rappresenta il coefficiente stechiometrico; (+) per i prodotti e (-) per i reagenti
La composizione del sistema è definita ad ogni istante dal parametro
ξ (grado di avanzamento)
ni° = sono le moli iniziali quando
il grado di avanzamento ξ = 0
ni = sono le moli quando il grado
di avanzamento assume il valore ξ
ovvero
Quindi ricordando che il coefficiente νi è positivo per i prodotti e negativo per i
reagenti, possiamo scrivere:
Per i reagenti
etc.
Per i prodotti
etc.
Tornando alla reazione e al (ΔG)T,P
aA + bB + cC... → lL + mM + nN...
Introducendo a
(dG )T ,P = (l G L d" + m G M d" + ...)! (a G A d" + b G B d" + ...)
(dG )T ,P = [(l G L + m G M + ...) " (a G A + b G B + ...)]d!
( dG %
&&
## = l G L + m G M + ... " a G A + b G B + ... = (!G )T , P
' d) $ T , P
[(
) (
)]
Nel progressivo avanzamento della reazione dG varia continuamente
al variare della composizione del sistema. La reazione procede
spontaneamente per come è stata scritta fin quando dG < 0
( dG %
&&
## = l G L + m G M + ... " a G A + b G B + ... = (!G )T , P
' d) $ T , P
[(
)]
) (
Energia libera di reazione
Se tutti i componenti sono nel loro stato standard
[(l G
o
L
o
)(
o
o
)]
(
+ m G M + ... " a G A + b G B + ... = !G o
)
T ,P
Energia libera standard di reazione
( dG %
&&
## = l G L + m G M + ... " a G A + b G B + ... = (!G )T , P
' d) $ T , P
[(
)]
) (
L'equilibrio chimico si raggiunge quando la funzione G assume il valore minimo
rispetto all'avanzamento della reazione; matematicamente questo significa
' dG $
%% d( "" = (!G )T , P = 0
&
#T ,P
[(l G
L
) (
)]
+ m G M + ... ! a G A + b G B + ... = 0
L'energie libere molari dei singoli componenti nella forma più generale è:
o
G i = G i + RT ln ai
("G )T ,P =
[(lG
("G )T ,P =
o
L
)(
o
o
)]
o
+ lRT ln a L + mG M + mRT ln aM + ... ! aG A + aRT ln a A + bG B + bRT ln a B + ...
[(lG
o
L
o
o
)
o
)]
(
+ mG M + ... ! aG A ! bG B ! ... + RT ln aLl + ln aMm + ... ! ln a Aa ! ln aBb ! ...
o
("G )T ,P = #$ i G i
(
)
+ RT ln aLl + ln aMm + ... ! ln a Aa ! ln aBb ! ...
i
l
m
("G )T ,P = ("G o )T ,P + RT ln aLa ! aMb ! ...
Isoterma di reazione di Van't Hoff
a A ! a B ! ...
All'equilibrio (!G)T,P = 0 quindi:
(#G )
o
T ,P
= " RT ln
a Ll ! aMm ! ...
a Aa ! a Bb ! ...
a Ll ! a Mm ! ...
=K
a Aa ! a Bb ! ...
Legge dell'equilibrio chimico o Legge dell'azione di massa
Esercizio
Per reazione di 1 mol di HCl e 0.5 mol di O2 secondo la reazione:
4 HCl + O2 ↔ 2Cl2 + 2 H2O
A 400 °C e P = 1 atm, all’equilibrio sono presenti 0.39 mol di Cl2. Si calcoli il KP della
reazione.
4 HCl +
mol iniziali
1
mol formate
mol consumate
4 : 2 = x : 0.39
0.78
mol all’equilibrio
0.22
O2 ↔
2Cl2 +
2 H2O
0.5
1 : 2 = y : 0.39
0.39
0.39
0.39
0.39 0.195
0.305
Ntot= 1.305
oppure
Per il Cl2
Per HCl
Per O2
0.39 = 0 + 2 ξ
nHCl = 1 - 4 ξ
nO2 = 0.5 - ξ
KP =
2
Cl 2
4
HCl
2
H 2O
P !P
P
! PO2
quindi ξ = 0.195
= 1- 4(0.195) = 0.22
= 0.5 - (0.195) = 0.305
= 42.21
PCl2 = PH2O = 0.2988
PHCl = 0.1686
PO2 = 0.2337
Torna