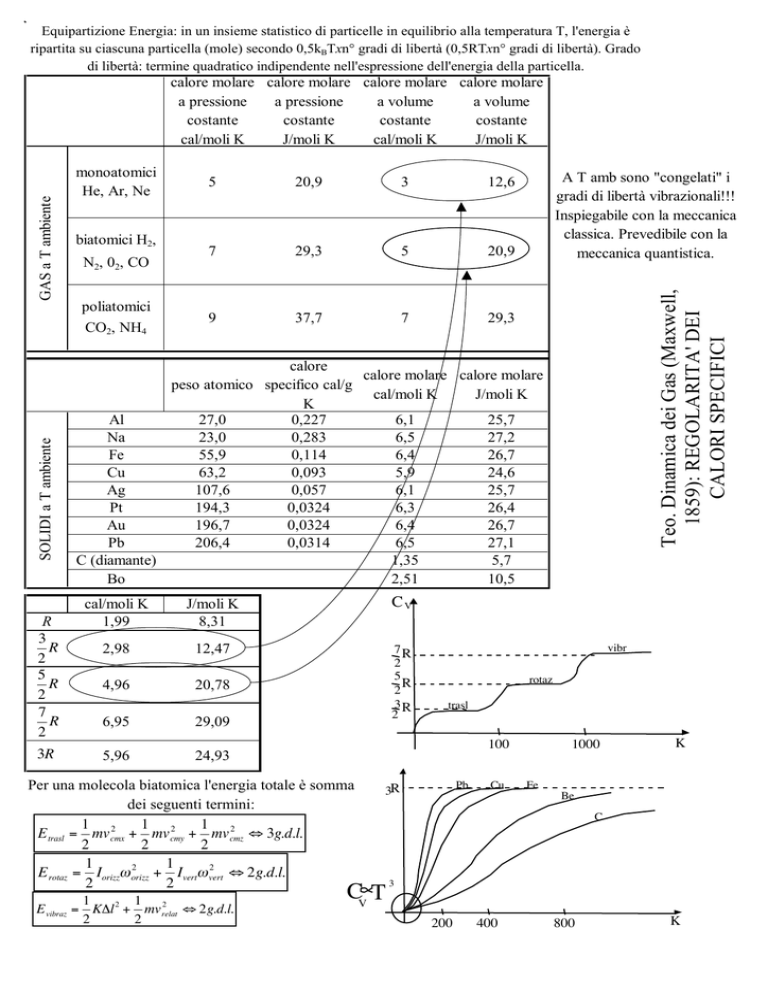
Equipartizione Energia: in un insieme statistico di particelle in equilibrio alla temperatura T, l'energia è
ripartita su ciascuna particella (mole) secondo 0,5kBTxn° gradi di libertà (0,5RTxn° gradi di libertà). Grado
di libertà: termine quadratico indipendente nell'espressione dell'energia della particella.
R
3
R
2
5
R
2
7
R
2
3R
monoatomici
He, Ar, Ne
biatomici H2,
N2, 02, CO
poliatomici
CO2, NH4
5
20,9
3
12,6
7
29,3
5
20,9
9
37,7
7
29,3
A T amb sono "congelati" i
gradi di libertà vibrazionali!!!
Inspiegabile con la meccanica
classica. Prevedibile con la
meccanica quantistica.
Teo. Dinamica dei Gas (Maxwell,
1859): REGOLARITA' DEI
CALORI SPECIFICI
SOLIDI a T ambiente
GAS a T ambiente
calore molare calore molare calore molare calore molare
a pressione
a pressione
a volume
a volume
costante
costante
costante
costante
cal/moli K
J/moli K
cal/moli K
J/moli K
calore
calore molare calore molare
peso atomico specifico cal/g
cal/moli K
J/moli K
K
Al
27,0
0,227
6,1
25,7
Na
23,0
0,283
6,5
27,2
Fe
55,9
0,114
6,4
26,7
Cu
63,2
0,093
5,9
24,6
Ag
107,6
0,057
6,1
25,7
Pt
194,3
0,0324
6,3
26,4
Au
196,7
0,0324
6,4
26,7
Pb
206,4
0,0314
6,5
27,1
C (diamante)
1,35
5,7
Bo
2,51
10,5
cal/moli K
1,99
J/moli K
8,31
CV
2,98
12,47
4,96
20,78
6,95
29,09
7R
2
5
R
2
3R
2
5,96
24,93
rotaz
trasl
100
Per una molecola biatomica l'energia totale è somma
dei seguenti termini:
1 2
1 2
1 2
E trasl = mv cmx
+ mv cmy
+ mv cmz
¤ 3g.d.l.
2
2
2
1
1
2
2
E rotaz = Iorizzw orizz
+ Ivertw vert
¤ 2g.d.l.
2
2
1
1 2
E vibraz = KDl 2 + mv relat
¤ 2g.d.l.
2
2
vibr
Pb
3R
CV T
Cu
1000
Fe
K
Be
C
3
200
400
800
K












