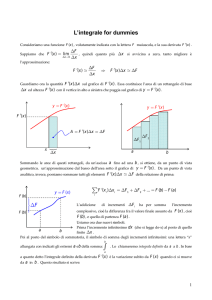
Integrale Indefinito
PROBLEMA: Data una funzione1 f : I → R, dove I :=]a, b[⊆ R, trovare una funzione
derivabile F : I → R, tale che F 0 (x) = f (x) per ogni x ∈ I.
Una tale funzione, se esiste, si chiama primitiva di f su I. Inoltre, da ora in poi, scriveremo
Z
F (x) = f (x) dx
(x ∈ I).
Ossia, per indicare la primitiva F di f (ma anche il problema stesso di trovare la primitiva
di f ) useremo il simbolo appena introdotto che viene usualmente chiamato integrale
indefinito di f .
Per prima cosa, si osservi che se F è una primitiva di f , allora anche F (x) + C è una
primitiva, per ogni (numero) C ∈ R. Pertanto, d’ora in poi, scriveremo, più precisamente
Z
F (x) + C = f (x) dx
∀ C ∈ R (x ∈ I).
Per molte funzioni, il problema precedente può essere risolto abbastanza facilmente. La
risposta, in effetti, per molte funzioni elementari, è fornita dalla tabella delle derivate
delle funzioni elementari, ma... letta al contrario!
Esempi.
• Partiamo da f (x) = a con a ∈ R fissato. Allora, è facile vedere che, posto F (x) = ax,
si ha sempre F 0 (x) = a. Pertanto
Z
a dx = ax + C.
• Più in generale, sia f (x) = xα con α ∈ R fissato. Ricordiamo preliminarmente che se
si considera la funzione g(x) = xβ , dove β ∈ R, si ha sempre g 0 (x) = βxβ−1 . Qual è
α+1
allora una primitiva di xα ? Essa è F (x) = xα+1 . Possiamo pertanto scrivere
Z
1
xα dx =
xα+1
+C
α+1
Notare che se si assume che f è continua, allora F dovrà essere di classe C1 .
• Sia f (x) = ex . Sappiamo che Dex = ex . Pertanto
Z
ex dx = ex + C.
Più in generale, consideriamo l’esponenziale in base a > 0 (a 6= 1), ossia f (x) = ax .
ax
Ricordando che Dax = log a · ax , segue subito che D log
= ax , ossia possiamo
a
sempre scrivere
Z
ax
x
a dx =
+ C.
log a
• Se f (x) = x1 dove I ⊆ R \ {0}, allora conosciamo già (!!!) una funzione la cui
derivata è f (x): infatti D(log |x|) = x1 . Pertanto
Z
1
dx = log |x| + C.
x
• Se f (x) = cos(x) conosciamo già una funzione la cui derivata è f (x): infatti
D(sin(x)) = cos(x). Pertanto
Z
cos(x) dx = sin(x) + C.
Analogamente, dato che D cos(x) = − sin(x), allora ne consegue che
Z
sin(x) dx = − cos(x) + C.
• Se f (x) = cosh(x) conosciamo già una funzione la cui derivata è f (x): infatti
D(sinh(x)) = cosh(x). Pertanto
Z
cos(x) dx = sin(x) + C.
Analogamente, dato che D cosh(x) = sinh(x), allora ne consegue che
Z
sinh(x) dx = cosh(x) + C.
1
• Se f (x) = 1+x
2 , come possiamo trovare una primitiva di f ? Basta ricordare che la
1
funzione arctan(x) ha per derivata f (x), ossia che D arctan(x) = 1+x
2 . Pertanto, si ha
Z
1
dx = arctan(x) + C.
1 + x2
• Se f (x) = cos12 (x) , come possiamo trovare una primitiva di f ? Basta ricordare che la
funzione tan(x) ha per derivata f (x), ossia che D tan(x) = cos12 (x) . Pertanto, si ha
Z
1
dx = tan(x) + C.
cos2 (x)
Analogamente2 , osservando che D(cot(x)) = − sin21(x) , segue subito che
Z
1
dx = − cot(x) + C.
sin (x)
2
1
• Se f (x) = √1−x
2 , come possiamo trovare una primitiva di f ? Basta ricordare che la
1
funzione arcsin(x) ha per derivata f (x), ossia che D arcsin(x) = √1−x
2 . Pertanto, si ha
Z
√
1
dx = arcsin(x) + C = − arccos(x) + C 0 ,
1 − x2
dove l’ultima uguaglianza è banale.
A questo punto, enunciamo le proprietà salienti dell’integrale definito.
Valgono le seguenti:
• (Linearità) Assumiamo che f, g : I → R sono funzioni che ammettono una primitiva.
Allora
Z
Z
Z
(αf + βg)(x) dx = α f (x) dx + β g(x) dx
∀ α, β ∈ R.
• (Principio di Sostituzione) Sia f : I → R derivabile. Sia ϕ : J → I una biiezione
(ossia, iniettiva e tale che ϕ(J) = I) e si assuma che ϕ ∈ C1 (J). Allora
Z
Z
f (x) dx = f (ϕ(t)) ϕ0 (t) dt.
• (Integrazione per Parti) Se f, g : I → R sono funzioni derivabili, si ha
Z
Z
0
f (x)g(x) dx = − f (x)g 0 (x) dx + f (x)g(x) + C
∀ C ∈ R.
2
Per definizione, cot(x) =
1
tan(x)
=
cos(x)
sin(x) .
La dimostrazione di queste prorietà è immediata3 , nelle ipotesi date. Si tratta solo di
applicare la definizione di primitiva. [Le rispettive proprietà che abbiamo enunciato
nel caso dell’integrale definito-di Riemann- invece sono meno banali e richiedono una
dimostrazione rigorosa, come fatto nelle dispense: interpretate queste di sopra come regole
“pratiche” che servono nel calcolo degli integrali.]
Enuncio di seguito una lista di primitive “immediate” (ma molto generali, visto che
si assume implicitamente che f è una qualsiasi funzione derivabile), che si ottengono
facilmente dalla regola di derivazione della funzione composta (ossia, con il principio di
sostituzione appena enunciato).
Di seguito4 C ∈ R è un’arbitraria costante reale.
•
Z
•
[f (x)]α f 0 (x) dx =
Z
[f (x)]α+1
+ C.
α+1
ef (x) f 0 (x) dx = ef (x) + C.
Più in generale, si ha
Z
•
•
Z
Z
af (x) dx =
af (x)
+ C.
log a
f 0 (x)
dx = log |f (x)| + C.
f (x)
cos(f (x))f 0 (x) dx = sin(f (x)) + C.
3
La prima (ossia la linearità) segue,
per definizione di integrale
indefinito,
R
R
R derivando ambo i membri:
d
d
d
infatti si ottiene (αf + βg)(x) = dx
(αf + βg)(x) dx = α dx
f (x) dx + β dx
g(x) dx = αf (x) + βg(x). La
seconda proprietà si può dimostrare come segue: partiamo dalla funzione f (ϕ(t))ϕ0 (t) e notiamo che una
sua primitiva è data dalla funzione F (ϕ(t)), dove F (x) è una primitiva di f (x) su I (ossia, F 0 (x) = f (x)
d
F (ϕ(t)) = F 0 (ϕ(t))ϕ0 (t) = f (ϕ(t))ϕ0 (t)
per ogni x ∈ I). Infatti, derivando in t tale funzione, si ottiene dt
(si osservi l’uso del teorema di derivazione della funzione composta, che si può adoperare, nelle ipotesi
fatte). D’altra parte, la primitiva a primo membro è proprio F (x) per ogni x ∈ I. La terza (formula
di integrazione per parti) infine segue derivando -regola di Leibnitz- il prodotto f (x)g(x). Si ottiene cioè
D(f (x)g(x)) = f 0 (x)g(x)+f (x)g 0 (x). Questa formula, valida per ogni x ∈ I, dice dunque che una primitiva
della funzione f 0 (x)g(x) + f (x)g 0 (x) è -banalmente- la funzione f (x)g(x). Ossia, una primitiva di f 0 (x)g(x)
si ottiene sommando di una primitiva di −f (x)g 0 (x) con la funzione f (x)g(x).
4
Chiaramente, alcune delle funzioni che appaiono, richiedono condizioni di esistenza che dovreste
cercare di formulare, se necessarie. Per esempio, nel terzo integrale indefinito, f (x) deve essere diversa da
0, etc..
Analogamente
Z
•
sin(f (x))f 0 (x) dx = − cos(f (x)) + C.
Z
cos(f (x))f 0 (x) dx = sin(f (x)) + C.
Analogamente
Z
•
sinh(f (x))f 0 (x) dx = cosh(f (x)) + C.
Z
•
f (x)
dx = arctan(f (x)) + C.
1 + [f (x)]2
Z
Analogamente
Z
•
Z
f 0 (x)
dx = tan(f (x)) + C.
cos2 (f (x))
f 0 (x)
dx = − cot(f (x)) + C.
sin2 (f (x))
f 0 (x)
p
dx = arcsin(f (x)) + C = − arccos(f (x)) + C.
1 − [f (x)]2