BE BE r

Fine
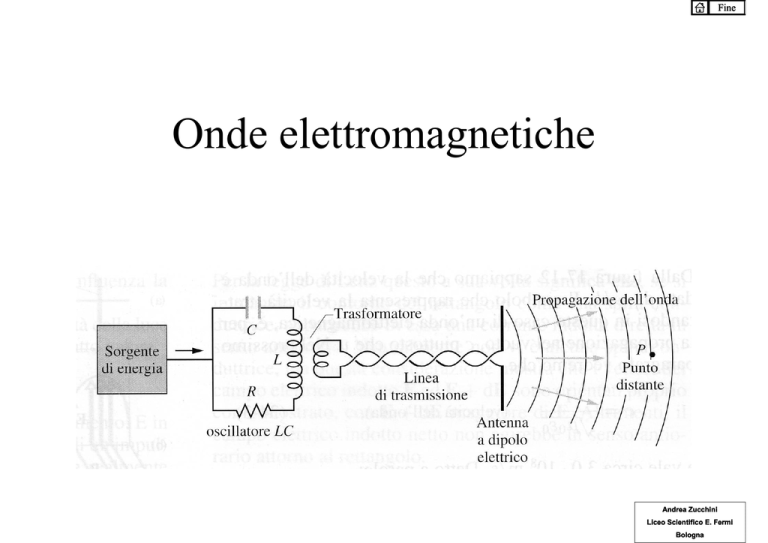
Onde elettromagnetiche
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Set di equazioni quasi “complete”
Legge di Faraday-Neumann
Teorema di Gauss per
()
()
r
Γ B = µ 0 ∑ ik
Teorema di Ampere
Teorema di Gauss per
()
r
r
dΦ S B
Γ E =−
dt
k
()
Cariche
elettriche
r
1
ΦS E =
r
E
r
B
()
ε0
r
ΦS B = 0
∑q
k
k
Cariche
magnetiche
assenti
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Set di equazioni quasi “complete”
Se non ci fossero le cariche elettriche si avrebbero
le equazioni
r
()
()
Legge di Faraday-Neumann
r
dΦ S B
Γ E =−
dt
Teorema di Ampere
r
Γ B =0
Teorema di Gauss per
Teorema di Gauss per
()
()
r
ΦS E = 0
r
E
r
B
Perché non c’è un
termine di variazione
del flusso del campo
elettrico ?
()
r
r
dΦ S E
≠0⇒Γ B ≠0
dt
()
()
r
ΦS B = 0
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Altri “indizi”
Cosa accade tra le armature di un condensatore ?
Considero il teorema di Ampere
()
r
Γ B ≠0
()
r
Γ B ≠0
()
r
Γ B =0
()
r
Γ B ≠0
C’è una forte discontinuità quando si passa al volume interno tra
r
r
le armature: Γ(B ) = 0 mentre lungo i conduttori si ha Γ(B ) ≠ 0
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Cosa accade tra le armature ?
Tra le armature di un condensatore, durante la carica
r
r
r
il campo elettrico varia passando da E a E + ∆E
Calcoloper
Applico
Divido
la
il teorema
variazione
l’intervallo
di di
Gauss
diflusso
tempo
Corrente di spostamento
r
r ∆Er 1r ∆q r 11
S ⋅ SS E== S ⋅ ∆E== i ∆q
∆Φ
∆t ε 0 ∆t ε ε0 0
()
()
r
∆Φ S E
i spostamento = ε 0
∆t
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Set di equazioni di Maxwell “complete”
()
Legge di Faraday-Neumann
r
r
dΦ S B
Γ E =−
dt
Teorema di Ampere
⎛
r ⎞
⎜
r
dΦ S E ⎟
⎟
Γ B = µ 0 ⎜ ∑ ik + ε 0
⎜⎜ {
k
142dt43 ⎟⎟
⎝ correnti reali corrente di spostamento ⎠
Teorema di Gauss per
Teorema di Gauss per
()
()
()
()
r
1
ΦS E =
r
E
r
B
ε0
∑q
k
k
()
r
ΦS B = 0
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Equazioni di Maxwell e onde elettromagnetiche
Consideriamo le equazioni di Maxwell in assenza di cariche e
correnti (reali !)
()
Legge di Faraday-Neumann
r
r
dΦ S B
Γ E =−
dt
Teorema di Ampere
r
r
dΦ S E
Γ B = µ 0ε 0
dt
()
()
()
()
Teorema di Gauss per
r
E
r
ΦS E = 0
Teorema di Gauss per
r
B
r
ΦS B = 0
()
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Le funzioni che descrivono campi elettrico e magnetico di un’onda EM
hanno la forma
r r
E = E0 sin (kx − ωt )
r r
B = B0 sin (kx − ωt )
o più in generale
r r
E = E ( x − ct )
r r
B = B(x − ct )
Dalle equazioni di Maxwell si ricava che i campi elettrico e magnetico
soddisfano le equazioni d’onda
r
r
2
∂ E 1 ∂ E
= 2 2
2
∂x
c ∂t
r
r
2
∂ B 1 ∂ B
= 2 2
2
∂x
c ∂t
2
2
La velocità della luce è legata a permeabilità magnetica del vuoto e
costante dielettrica del vuoto
c=
1
ε 0 µ0
≈ 3 ×108
m
s
()
r
r
1 dΦ S E
ΓB = 2
dt
c
()
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
r r
E×B
rˆ = r r
E×B
Considero la direzione dell’onda
•
Campi elettrici e magnetici sono sempre perpendicolari alla
direzione di avanzamento dell’onda
r
E ⊥ rˆ
r
B ⊥ rˆ
•
Campi elettrici e magnetici sono perpendicolari tra loro
•
Il rapporto fra i campo elettrico e magnetico è pari alla velocità della
r
luce
r r
E⋅B = 0
E
r =c
B
Il vettore di Poynting misura la quantità di energia per unità di
tempo e area
r 1 r r
S=
E×B
µ0
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
File Mathematica onde EM
0
5
10
15
20
0
5
5
10
15
20
5
5
0
0
0
-5
-5
-5
5
0
-5
-5
-5
0
0
0
5
2.5
5
5
7.5
5
10
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna
Fine
Ulteriori caratteristiche delle onde
elettromagnetiche
• Le onde EM possono essere polarizzate
• Le onde EM seguono le leggi di
–
–
–
–
Riflessione
Rifrazione
Interferenza
Diffrazione
http://mitglied.lycos.de/radargrundlagen/antennen/at07-de.html
Andrea Zucchini
Liceo Scientifico E. Fermi
Bologna