La Probabilità

La Probabilità
2. Il concetto e la definizione
Il concetto di probabilità è un concetto istintivo della nostra mente e può essere applicato in tutti
quei fenomeni in cui fornire una risposta deterministica risulta impossibile, mentre si può ipotizzare
per ogni valore solo un ordine di priorità.
La probabilità definisce questa scala di priorità attribuendo ad ogni singolo evento un numero
compreso tra φ ed 1.
Il riscontro nella realtà fisica di innumerevoli fenomeni che se pur aleatori manifestano un grado di
priorità, consente di comprendere in pieno il concetto di probabilità.
Diversa è la situazione per la definizione di questo ente che in termini matematici può essere fornita
compiutamente solo in termini assiomatici.
2.1 Definizioni
I tentativi per definire questo ente sono stati numerosi e tra questi vale la pena di ricordare quello di:
a) Laplace
Si individuano le classi di simmetria dell’evento ad esempio:
Evento
Lancio di due monete uguali
Simmetrie
cc, tt, ct, tc
Le classi non sono distinguibili e ad ognuna di esse si assegna il valore 0.25.
b) Von Mises
Probabilità evento A = lim
N
∞
NA
dove
N
N sono i casi possibili, ed NA i casi che manifestano la proprietà A.
1
Ad esempio:
Evento A
uscita del n.2 nel lancio di un dado
Probabilità evento
lim
N
∞
NA
= 1/6
N
Entrambe queste definizioni presentano dei limiti, infatti la prima cade in difetto perché non è
sempre possibile conoscere le classi di simmetria, la seconda perché non è detto che se faccio 1000
lanci non esca mai il 2.
Definizione Assiomatica della Probabilità
La definizione si basa sul soddisfacimento degli assioni cui la probabilità deve obbedire.
Sia S un insieme di eventi (discreto o continuo) e ad ognuno di essi è possibile associare un numero
P, tra φ ed 1, nel rispetto dei seguenti assiomi.
-
Non esistono valori negativi perché sarà sempre
P(A) ≥φ
-
Se un evento è certo sarà
P(A) = 1
-
Se un evento è impossibile sarà
P(A) = φ
-
Se due o più eventi sono mutuamente esclusivi, sarà
P(AUB) = P(A) + P(B)
In coerenza con la definizione assiomatica della Probabilità è possibile associare ad essa altri due
concetti importanti :
-
La densità di probabilità
-
La funzione di distribuzione
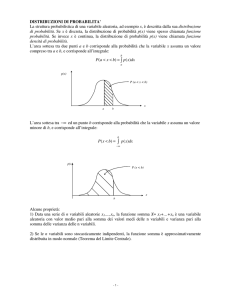
Infatti con riferimento alla fig. n. 1 in cui è rappresentata una funzione y=ƒ(x) nell’intervallo a, b, se
l’area contenuta tra la curva e l’intervallo è pari ad 1 la y=ƒ(x) sarà una curva di densità, infatti:
2
P = ∫ f ( x) ⋅ dx
fig.1
-
non esiste possibilità che si verifichi un evento al di fuori di a,b:
P(φ) =φ
-
è certo che si possa verificare un evento in (a,b)
P(S) = 1
-
i valori di dP = f(x) ⋅ dx sono positivi sempre:
f(x) ≥ φ
-
eventi mutuamente esclusivi determinano
P(x1+x2) = P(x1) + P(x2) = f1(dx1) + f2(dx2)
Pertanto la y= f(x) è una curva di densità di probabilità.
Se integro la y= f(x) in un intervallo (a,∈)
ε
ottengo
F=
∫
a
f ( x)dx
La F prende il nome di distribuzione di probabilità e risponde alla domanda “Qual è la probabilità
che si verifichi un evento tra a ed ∈” (fig. n.2)
3
Fig.2
Questa probabilità è rappresentata dall’area tratteggiata
E’ evidente che
F(x) =
∫
b
a
f ( x)dx = 1
fuori dall’intervallo sarà
F(x) = φ
Pertanto mentre la densità di probabilità è riferita ad un punto sull’asse reale x, la funzione
distribuzione presume un intervallo.
2.2 Teoremi sulla probabilità
Vedremo meglio nel seguito che la v.c. “misura” si distribuisce secondo la legge di Gauss
rappresentata in figura
4
Per ora diremo soltanto che la curva è simmetrica rispetto ad un valore centrale µ che è la media
delle misure e che, in un buon sistema di misure, la probabilità che si presentino valori molto
discosti dalla µ è piccola, mentre la probabilità che si presentino valori prossimi alla µ è più alta,
infatti ƒ1 << ƒ2
La densità di probabilità ƒ è espressa dalla
f =
1
2π ⋅ σ
⋅e
−
( x−µ )2
2⋅σ 2
Pertanto se di una popolazione conoscessi a priori la media µ e la varianza σ2 potrei tracciare la
curva ƒ.
Supponiamo che la curva sia quella in fig.
Se volessi conoscere la probabilità che si presenti una misura tra i valori a e b, basterà conoscere
l’area compresa tra la curva e l’intervallo a,b.
5
2.3 Teorema della probabilità totale
Continuando ad utilizzare la curva di Gauss supponiamo di aver misurato l’angolo AôB con la
precisione del 1”
e che la curva teorica di distribuzione degli scarti (errori) sia quella in figura.
Se vogliamo conoscere la probabilità che si presenti un errore tra 2” e 3” (negativo), basta che
determini l’area A compresa tra la curva e l’intervallo richiesto.
Analogamente se voglio conoscere la probabilità tra 5” e 6” (positivo).
E’ chiaro che la probabilità che si presenti un errore tra 2” e 3” (negativo) o tra 5” e 6” sarà
P=A+B
Questa è l’espressione della probabilità totale nel caso che i sottoinsiemi di misure siano disgiunti:
6
Vediamo il caso in cui i due sottoinsiemi presentano un’intersezione:
A∨B
= (A-B) ∨ B
P(A∨B) = P(A-B) + P(B)
P(A-B) = P(A) – P (A∧B)
P(A∨B) = P(A) + P(B) – P(A∧B)
P (0” ÷ 2”) = a + b
P(1” ÷3”) = b + c
P (1” ÷ 2”) = b
P (0” ÷ 3”) = (a + b) + (b + c) – b = a + b + c
2.3.1 La probabilità condizionata
In alcuni casi i valori argomentali possono essere classificati con due distribuzioni di probabilità
diverse, ed in questi casi è importante vedere se tra le due distribuzioni c’è o meno una
correlazione.
7
Vediamo di spiegarci con un esempio.
Supponiamo che di un fabbricato che si è instabilizzato sono stati tenuti in osservazione 100 punti,
nei quali si sono misurati al tempo t1 gli spostamenti δ e rotazioni ϕ, riassunti nella tabella
seguente:
ϕ
+
-
ƒ(δ)
+
20
10
0.3
-
40
30
0.7
ƒ(ϕ)
0.6
0.4
1
δ
Da questo set di misure posso dire che:
1) La priorità con cui si presenta
P(δ+ ϕ+) = 0.20
P(δ+) = 0.3
P(δ+ ϕ-) = 0.10
P(δ-) = 0.7
P(δ- ϕ+) = 0.4
P(ϕ+) = 0.6
P(δ- ϕ-) = 0.3
P(ϕ-) = 0.4
e posso anche affermare che se si è verificata una ϕ+ , la priorità con cui si presenta
δ+ = 20/60 = 1/3 = 0.333
δ- = 40/60= 2/3 = 0.666
Queste due valutazioni sono condizionate dal fatto che ho ristretto le priorità di δ a quella di ϕ
già verificatasi come positiva.
8
In coerenza all’esempio potremo scrivere
P (δ+ . ϕ+)
P (δ+ / ϕ+) = ------------
vale a dire
P(ϕ+ )
“La priorità con cui si può verificare uno spostamento (+) una volta che si è verificata una
rotazione (+) è data dalla priorità dell’insieme intersezione (δ+ , ϕ+) divisa per la priorità che si
verifichi una ϕ+ nell’intera popolazione infatti:
20/100
P (δ+ / ϕ+) = ------------ = 20/60 = 1/3
60/100
Domandiamoci ora se tra gli eventi riportati in tabella vi sia un legame, notiamo infatti che
correlando la qualità di uno spostamento alla qualità di una rotazione il valore cambia rispetto a
quelli presi in assoluto.
Se però
P (A/B) = P (A)
vale a dire se la probabilità condizionata di A rispetto a B fosse sempre
uguale ad P (A), gli eventi A e B sarebbero indipendenti.
Supponiamo che la tabella precedente assumesse i valori seguenti:
ϕ
δ
+
-
ƒδ
+
20
20
0.4
-
30
30
0.6
ƒϕ
0.5
0.5
1
Avremo che P(δ+ ) = 40/100 = 0.4
P(δ+ / ϕ+)
ma anche P (δ+ / ϕ+) = ------------ = 0.2/0.5 = 0.4
P(ϕ+)
9
quindi il fatto che si sia verificata una ϕ+ non condiziona il risultato di δ+
il che significa che δ+ è indipendente da ϕ+
2.3.2 La probabilità composta
Si definisce probabilità composta quella dell’evento che contemporaneamente appartiene a due
insiemi:
δ+ ϕ+
probabilità composta P(δ+ ϕ+)
Nel caso in cui gli eventi sono indipendenti
Sarà P(δ+ ϕ+) = P(δ+) x P(ϕ+)
Come è facile dimostrare, infatti se:
P(δ+ ϕ+)
P(δ+ / ϕ+) = --------------- = P(δ+)
P(ϕ+)
P (δ+ ϕ+) = P(δ+) x P(ϕ+)
10
3 La variabile casuale e la variabile statistica
3.1 Il concetto
Le due entità matematiche che stiamo per introdurre sono aspetti diversi della stessa realtà
operativa, nel senso che mentre la prima (v.c.) propone una ipotesi di realtà, la seconda (v.s.)
registra gli effetti accaduti.
Riferendoci alle misure potremo dire che con la (v.c.) è possibile eseguire un progetto della misura
stessa, mentre con la (v.s.) ne collauderemo il risultato.
La prima propone un modello, la seconda ne verifica la bontà ed il nesso che le unisce non potrà che
essere di tipo stocastico.
Data la diversa natura sul piano operativo, diversa sarà anche la definizione matematica, infatti
mentre la v.c. altro non è che una funzione di distribuzione di probabilità, la v.s. è invece il rapporto
tra gli eventi verificatisi e quelli possibili.
Sia la v.c. che le v.s. possono essere n dimensionali, le definizioni che seguono si riferiscono a
variabili monodimensionali, ma questo non ne limita la generalità.
3.2 La definizione matematica
Riferendoci al caso monodimensionale diremo che la v.c. è una distribuzione di probabilità sulla
retta reale.
La v.c. è definita da
F(xo) = P(x ε Ixo)
(a)
x2
x
Ixo
La funzione distribuzione gode delle seguenti proprietà:
1) F(xo) è definita per ogni xo reale 0 ≤ F(xo) ≤ 1
2) Lim F(xo) = φ
xo
-∞
11
x1 1
3) Lim F(xo) = 1
xo
4) F(x2) ≥ F(x1)
x2 ≥ x1
∞
Una v.c. può essere discreta:
1
2
3
4
può essere continua
la v.s. è invece definita da una tabella a due righe di valori numerici
x1
x2……………….xn
N1
N2……………….Nn
Nella prima riga si riportano i valori argomentali, mentre nella seconda si scrivono i numeri che
rappresentano le frequenze assolute
Il numero ∑ni=1 Ni rappresenta la numerosità della popolazione
Si definisce frequenza ƒi il termine
ƒi = Ni / N
e rappresenta
il numero di volte che si presenta il valore argomentale xi.
3.3 Confronto tra v.s. e v.c.
Il confronto tra v.c. e v.s. costituisce la base del trattamento dei dati, questo confronto potrebbe
avvenire attraverso una sovrapposizione degli istogrammi che descrivono la v.s. con le curve che
definiscono la v.c.
12
Ma in effetti si preferisce ricorrere al confronto attraverso i parametri statistici, che nel caso delle
misure si limitano ad essere la media e la varianza. Infatti per le nostre applicazioni quello che conta
sapere è dove si concentra la distribuzione e quale sia la dispersione attorno al punto di massima
concentrazione.
3.4 La Media
Questo parametro fornisce il valore attorno a cui si concentra la distribuzione della popolazione,
traslando il concetto in termini meccanici potremo dire che la media è il baricentro della
popolazione, conseguentemente la sua espressione è data da:
M(x) =
∫
x ƒ(x) dx (caso continuo)
M(x) = 1/n ⋅ ∑xi
(caso discreto)
Volendo differenziare il caso in cui si tratta di v.c. o v.s., scriveremo
- µ(x)
che indica una media per v.c.
- m(x)
che indica una media per v.s.
- M[.]
è l’operatore di media.
Esempio n.1
Sia data la funzione densità in figura
f
c
1
x
1
2
13
ƒx =
o≤ x ≥ 2
altrimenti
½x
φ
a) Vogliamo verificare se ƒx è una funzione densità di probabilità, se è vero, dovrà essere
2
∫f
( x)
dx = 1
0
sostituendo il valore di ƒx avremo
2
∫
1
2
x dx = [ 1 4 x 2 ]02 = 1
0
quindi ƒ(x) è una funzione densità di probabilità
b) Calcoliamo la media
2
2
0
0
µx = ∫ x f (x) dx = ∫ x 1 2 x dx = ∫ 1 2 x 2 dx = [x 3 / 6]02 = 4 / 3
In effetti se ci riferiamo alla media come valore baricentrico si ha che su x risulterà
x = 2/3 ⋅ 2 = 4/3
Possiamo fare ancora un’altra verifica, considerando la mediana C1 che ha equazione
x–1
y-φ
-------- = ---------2–1
1-φ
Se intersechiamo la C1 con la retta x =4/3 avremo:
y = 4/3 – 1 = 1/3
che è proprio l’ordinata del baricentro.
14
y=x-1
3.4.1 Proprietà della media
Cosa ci interessa sapere sulla media?
1) Se la distribuzione è simmetrica qual è il valore della media ?
ƒ(c+h) = ƒ(c-h)
∞
∞
∞
∞
∞
-∞
−∞
-∞
µx = ∫ (c + h) ⋅ f (c + h) = ∫ c ⋅ f (c + h) + ∫ h ⋅ f (c + h) = c ∫ f (c + h) + φ = c
2) Se tra le due v.c. y ed x esiste un legame lineare, la media lo rispetta infatti
y = ax + b
M[y] = a M[x] + M[b] = a M[x] + b
Consideriamo la particolare variabile scarto definita da
ν = x - µx
la media sarà
M[ν] = M[x] – M[µx] = µx - µx = φ
15
Variabile casuale funzione di un’altra
Tra le variabili casuali x e y esiste il seguente legame funzionale
Y = g (x)
Si vuole calcolare la ƒy conoscendo la ƒx
La funzione g(x) è definita nell’insieme Sx e trasforma δx nella corrispondente immagine Sy.
Se Ay è un sottoinsieme (intervallo) di δy, esisterà un sottoinsieme Ax tale che
g(Ax) = Ay
Si pone per definizione che
P(y ∈ Ay) = P(x ∈ Ax)
Ad esempio se
Ay = c ≤ y ≤ d
⇒ Ax = x 1 ≤ x ≤ x 2
e x3 ≤ x ≤ x4
Se passiamo ad intervalli infinitesimi avremo che all’intervallo ay = dy (yo)
ax = ki dx (xi)
È sarà
P(y ∈ dyo) = ∑P (x ∈ dxi)
16
corrisponderanno
i = 1, 2, 3…….
Sappiamo che per una variabile casuale i valori di P (probabilità) ed f (densità) sono numeri
positivi al più nulli, pertanto si avrà:
P( x ∈ dx) = fx dx
dove con | dx | si indica il valore assoluto dell’intervallo dx.
Avremo così:
P( y ∈ dy)
P( x ∈ dxi)
P (x ∈ dxi) 1
=∑
=∑
⋅
dy
| dy |
| dy |
| dx |
dx
sarà così
fy = ∑
fx
ove f x = f [ g −1 ( y )]
g '⋅( x)
Esempio n.1
fx
La distribuzione della x è quella in figura con
ƒx=1/2 e µx = 1
1/2
0
2
x
Tra y e x esiste la seguente relazione
y=x+5
(5 ≤ y ≤ 7)
pertanto, applicando la relazione precedente,
1
fx
fy =
= 2 = 1/ 2
g '⋅( x) 1
17
Avremo così
fy
1/2
5
7
y
7
y
2
µy = ∫ ⋅ dy =
5
y 2 49 − 25
=
=6
4
4
come del resto era prevedibile essendo la media un operatore lineare
µy = µx + b = 1 + 5 = 6
Esempio n.2
fx
1
2
x
y=x+5
fx 1
=
x 2
fx =
x
2
2
µx = ∫
0
x
y−5
fy = 2 =
;
1
2
7
y −5
µy = ∫ y ⋅
⋅ dy =
2
5
7
∫(
5
18
x2 x3 4
=
= = 1,33
2
6 3
(5 ≤ y ≤ 7)
y2 5y
− ) ⋅ dy = 6,33
2
2
Esempio n.3
fx
2/π
π/2
0
x
y = sen x
y’ = cos x
cos x = 1 − sen 2 x =
1- y2
fx = 2/π
µx = π/4
2
fx
fy =
=
| g' x |
π
(0 ≤ y ≤ 1)
1- y2
fy
2/π
µ(y)
0
1
Vediamo intanto se ƒy è una funzione densità:
1
∫
1
fy dy =
0
2
2 π
= [ ⋅ arc sen y ]10 = = ⋅ [ − 0] = 1
π
π 2
1− y2
2
1
∫π ⋅
0
Calcoliamo la media di y:
1
µy = ∫
0
2
π
⋅ y⋅
µy =
2
π
1
1− y
2
=
⋅ [φ + 1] =
19
2
π
2
π
⋅ [− 1 − y 2 ]10 =
= 0.636
Se calcoliamo la media di y come
µy = g (µx)
avremo
µy = sen(π/4) = 0.707
che è diversa da quella corretta precedentemente calcolata.
La diversità dei valori dipende dal fatto che la Variabile x non è concentrata in un intervallo in cui
g(x) è regolare.
Se supponiamo di stringere l’intervallo e cambiare densità per la x, avremo:
fx
4/π
π/4
0
x
fy =
4
(0 ≤ y ≤ 0.707)
π ⋅ 1- y2
µx = π/8
µy =
4
π
0.707
⋅
∫
0
y
1− y
2
=
4
π
⋅ [− 1 − y 2 ]00.707 =
4
π
⋅ (−0.707 + 1) =0.373
µy = g(µx) = sen (22°,5) = 0.382
µy ≈ µx
Esempio n.4
fx
4/π
y = sen x
fx
0
x
y’ = cos x
π/2
µx =2/3 ⋅ π/2 = 60°
x
20
4
fx π
=
x π
2
fx =
8
8
2
⋅x
π2
fy = π
=
g ' ( x)
8
⋅x
π2
⋅ arc seny
1− y2
Vediamo se la ƒy è una funzione di densità:
1
∫
∫
in quanto
arc seny
1- y2
1
8
arc seny
0
∫π
⋅ dy
è del tipo
fy dy =
2
⋅
1- y2
0
⋅ dy
∫ u dv = u ⋅ v - ∫ v du
1
è il differenziale di arc sen y, si ha così
1− y2
∫
arc seny
1- y2
⋅ dy = arc seny ⋅ arc seny - ∫
arc seny
1- y2
⋅ dy
da cui si ottiene che
2∫
arc seny
1- y2
= (arc seny) 2 ⇒ ∫
arc seny
1- y2
=
1
(arc seny) 2
2
Pertanto
1
∫
fy ⋅ dy =
0
1
4 π2
2 1
⋅
⋅
[(
)
]
=
⋅[
−φ] = 1
arcseny
0
π2 2
π2 4
8
La ƒy è una funzione densità.
Calcoliamo la media di y:
µy =
8
π
2
1
⋅∫ y⋅
0
21
arcsen y
1− y2
⋅ dy
essendo
y
1− y
2
∫ u dv = u ⋅ v - ∫ r ⋅ du
1
∫ y⋅
0
= d (− 1 − y 2 )
avremo
pertanto
arcsen y
1− y2
1
⋅ dy = [arcsen y ⋅ (− 1 − y )] − ∫
2
1
0
(− 1 − y 2 )
0
µy =
8
π
2
8
π2
1− y2
⋅ [− 1 − y 2 ⋅ arcsen y + y ]10 =
⋅ [φ + 1 + 1 ⋅ φ + φ ] =
8
π2
= 0.811
Dimostriamo ora l’importante teorema della media:
Se due variabili casuali x e y sono legate dalla relazione y =g(x) avremo:
µy = M [ y ] = M[g(x)]
Infatti se y = g(x) è funzione monotona crescente avremo g’(x) > φ e
fy =
fx
g ' ( x)
M [ y] =
con x = g-1(y)
∞
∞
−∞
-∞
∫ y f(y) dy = ∫ y ⋅
∞
= ∫ g(x) f x dx
-∞
= M[g(x)]
22
fx
dy =
dy
dx
⋅ dy
Esempio:
fx =
2 /π
φ ≤ x ≤π /2
x < φ x > π /2
φ
Abbiamo già visto che se y= senx la µy = 2/π.
Calcoliamo questa media utilizzando il teorema della media
π /2
µ y = µ x = M [ gx] =
∫ g ( x) fx dx =
φ
π /2
2
∫ senx ⋅ π ⋅ dx =
φ
2
π
⋅ [− cos x]πφ / 2 =
Se la v.c. x è molto concentrata ed in un intorno è possibile che
g(x) = g(µx) + (x - µx) ⋅ g’(µx)
potremo scrivere
µy =
∫
[g(µx) + (x - µx) ⋅ g’(µx)] ⋅ ƒx dx
µy =
∫
g(µx) ⋅ ƒx dx +
= g(µx)
∫
∫
(x - µx) ⋅ g’(µx)⋅ ƒx ⋅ dx =
ƒx dx + g’(µx)
∫
(x - µx) ⋅ ƒx ⋅ dx = g(µx)
In quanto il secondo termine è una media di scarti.
L’ipotesi di concentrazione della variabile è fondamentale, in quanto diversamente
µ(y) ≠ g (µx)
23
2
π
Facciamo un esempio semplice, considerando che sull’asse x la variabile possa assumere i valori
riportati in figura
1
2
3
4
5
6
7
8
9 10
e che sia y = x2 il legame funzionale;
la media dei valori sull’asse x vale
µx = 5.5 e se fosse vero che
µ(y) = g(µx)
avremo
µ(y) = 5.52 = 30.25
Se facciamo la media dei quadrati riportati sull’asse otterremo
µ(y) = 38.5 che è diversa da g(Mx)
proprio perché la distribuzione non è concentrata
Viceversa consideriamo la distribuzione
1
1.1
1.2
1.3
1.4
1.5
che è una distribuzione abbastanza concentrata la cui media vale µx = 1.25
Se il legame è sempre del tipo y=x 2 avremo:
1
1.21
1.44 1.69
la cui media vale µy = 1.59;
1.96
2.25
M[µx2] = M[1.252] = 1.56
1.5.2 La Varianza
Se consideriamo le due popolazioni in figura, ci rendiamo conto che pur avendo la stessa media µx,
sono distribuite in maniera diversa, ed in particolare la distribuzione (1) è molto più concentrata
della (2).
24
La concentrazione attorno al valore medio è un parametro statisticamente importante in quanto
segnala, nel caso di una popolazione di misure, maggiore o minore incertezza.
Questo parametro prende il nome di Varianza ed è definita da:
σ2 =
∫
(x - µx)2 ƒ(x)dx
(caso continuo)
σ2 = 1/n ∑ni=1 (x-µx)2
(caso discreto)
Nel caso in cui tra due v.c. y ed x esiste una relazione del tipo
y = g(x)
con g(x) funzione qualunque avremo:
σ2 (y)= [g’(x)]2 σ2x
σ2 (y) =
∫
(y-µy)2 ƒ(y)dy =
infatti
∫
[g(x) – µy]2 ƒ(x)dx
ma nell’ipotesi che la v.c. x sia concentrata attorno alla media µx e che g(x) sia regolare in questo
intorno, sarà:
g(x) = g(µx) + g’(µx) (x- µx)
σ2 (y) =
ma essendo g(µx) = µy
∫
quindi
[g(µx) + g’(µx) (x-µy) - µy]2 ƒ(x) dx
avremo
25
σ2 (y) =
∫
[g’(µx)]2 ⋅ (x-µx)2 ƒx dx = g’(µx)2 σ2x
il Valore ± √σ2 prende il nome di scarto quadratico medio (s.q.m.) ed ha il significato dello scarto
mediamente attribuibile ad ogni valore della popolazione.
Il termine Error medio della media (E.m.m.) è invece lo scarto attribuibile a µx e vale
σm = σ2 / √n
infatti
mx =
x
x1 x 2
+
+ ....... n
n
n
n
pertanto
2
2
σ 
σ1  σ 2 
 +   ....... n 
 n   n 
 n 
2
σ 2 ( m) = 
Le σi provenendo dalla stessa popolazione saranno tutte uguali, sarà così
σ 2 ( m) =
n
σ2
2
⋅
=
σ
n
n2
c.v.d.
Definizione di una variabile standardizzata
Si definisce standardizzata una variabile del tipo z = [x – µ(x)] / σ
Questa variabile ha le seguenti proprietà:
σ2 (z) = 1
M (z) = φ
Infatti
x – µ(x)
M(z) = M ------------------ =
σ
(x – µx)2
σ (z) = M [---------------]
σ2
2
26
M(x – µx)
-------------- = φ
σ
=
σ2 / σ2 = 1
Media Ponderata
Supponiamo di aver misurato la grandezza A con n diversi sistemi di misura, caratterizzati ognuno
da una varianza σi2:
Misura di A
σ12
σ22
σ32
……
σn2
X1
X2
X3
…
Xn
Potremo pensare che ciascun sistema sia un’estrazione di misure da popolazioni diverse la cui
media è M e che questa tende ad A che è il valore vero.
La tendenza ad A si esplica con varianze σi2 diverse.
Se scrivessimo
µx
= 1/n ∑ Xi
troveremmo un valore medio che non tiene conto di σi2, dobbiamo quindi trovare un indice αi tale
che
µ(x)
= ∑ αi Xi
1) µx = µ
tenuto conto
; 2) σi2 = min
questo significa che
µ (x) = M [∑ αi xi] = ∑αi ⋅ M[xi] = µx ⋅ ∑αi
∑αi = 1
deve essere inoltre σ2 (x) = ∑ αi2 σi2 = min
Quindi si deve cercare il minimo di ∑αi2 σi2 con la condizione ∑αi = 1
ƒ = ∑αi2 σi2 - λ ( ∑ αi - 1)
27
ϑƒ
------ = 2 αi σi2 - λ = φ
ϑαi
Posto 1/σi2 = Pi
sarà
λ
αi = ----2σi2
λ Pi
αi = -----2
E dovendo essere ∑αi = ∑ λ/2 Pi = 1
λ/2 = 1 / ∑ Pi
αi = Pi / ∑ Pi
pertanto avremo
∑ Pi xi
µx = ---------∑ Pi
e la varianza
∑ Pi2 σi2
σ2(x) = --------------(∑ Pi)2
Esempio
Si è misurato un angolo con due strumenti diversi
1) α1 = 37°,2711 ± 3”
σ1 =± 3”= ± 1,45x10-5 rad
2) α2 = 37°,2725 ± 5”
σ2 =± 5”=± 2,42x10-5
σ12 = 2,11x10-10
σ22 = 5,88x10-10
Posto P1 = 1 e ragguagliando i pesi si ha P2 = 0.36
0.2711 x 1 + 0.2725 x 0.36
α = 37° + -------------------------------- = 37°,2715
1.36
Calcolo della varianza pesata:
∑ P ⋅σ
(α ) =
(∑ P )
2
σ
2
i
2
i
2
i
=
12 ⋅ (1.45 ⋅ 10 −5 ) 2 + 0.36 2 ⋅ (2.42 ⋅ 10 −5 ) 2
= 1.55 ⋅ 10 −5
(1 + 0.36) 2
28
Teorema di Tchebycheff
Quale che sia la forma di una distribuzione di una v.c., la quasi totalità dei suoi valori argomentali
cade tra
- 3 σx ≤ x ≤ 3 σx
Infatti se consideriamo l’espressione della varianza
σ 2 = ∑ ( xi − µx ) 2 ⋅ fi = ∑υ i2 ⋅ fi
σ 2 = υ12 ⋅ f1 + υ 22 ⋅ f 2 + υ 32 ⋅ f 3 .......υ n2 ⋅ f n
in cui
νi
è lo scarto iesimo.
Supponiamo di fissare un valore νm dello scarto, al disotto del quale gli scarti siano nulli e al di
sopra siano tutti ugauli a νm.
ν1
ν2
φ
φ
ν3
νn
........
φ
νm
νm
νm
σ 2 = ∑υ i2 ⋅ f i > υ m2 ⋅ ( f m + f m +1 ..... ⋅ f n
ψ
ψ è la somma delle frequenze degli scarti superiori a νm, pertanto la somma delle frequenze ƒ
degli scarti inferiori a νm sarà:
ƒ=1-ψ
ψ=1-ƒ
σ 2 ≥ υ m2 ⋅ψ = υ m2 ⋅ (1 − f )
29
⇒ 1- f ≤
σ2
υ m2
e quindi
f > 1−
σ2
υ m2
il che significa che la frequenza degli scarti inferiori a νm è maggiore di 1 −
Poniamo ora
νm = λ ⋅ σ
avremo
f > 1−
σ2
1
= 1− 2
2
2
λ ⋅σ
λ
che è la disuguaglianza di Tchebycheff
(λ>1)
se poniamo
Vm = 2 σx
avremo
f > 1−
se poniamo
1
= 0.75
4
Vm = 3 σx
avremo
f > 1−
1
≅ 90%
9
30
σ2
υ m2