Continuando ad utilizzare la curva di Gauss supponiamo di aver

La Probabilità
2. Il concetto e la definizione
Il concetto di probabilità è un concetto istintivo della nostra mente e può essere applicato in tutti
quei fenomeni in cui fornire una risposta deterministica risulta impossibile, mentre si può ipotizzare
per ogni valore solo un ordine di priorità.
La probabilità definisce questa scala di priorità attribuendo ad ogni singolo evento un numero
compreso tra  ed 1.
Il riscontro nella realtà fisica di innumerevoli fenomeni che se pur aleatori manifestano un grado di
priorità, consente di comprendere in pieno il concetto di probabilità.
Diversa è la situazione per la definizione di questo ente che in termini matematici può essere fornita
compiutamente solo in termini assiomatici.
2.1 Definizioni
I tentativi per definire questo ente sono stati numerosi e tra questi vale la pena di ricordare quello di:
a) Laplace
Si individuano le classi di simmetria dell’evento ad esempio:
Evento
Lancio di due monete uguali
Simmetrie
cc, tt, ct, tc
Le classi non sono distinguibili e ad ognuna di esse si assegna il valore 0.25.
b) Von Mises
NA
Probabilità evento A =
lim
N
dove

N
N sono i casi possibili, ed NA i casi che manifestano la proprietà A.
1
Ad esempio:
Evento A
uscita del n.2 nel lancio di un dado
NA
Probabilità evento
lim
N

= 1/6
N
Entrambe queste definizioni presentano dei limiti, infatti la prima cade in difetto perché non è
sempre possibile conoscere le classi di simmetria, la seconda perché non è detto che se faccio 1000
lanci non esca mai il 2.
Definizione Assiomatica della Probabilità
La definizione si basa sul soddisfacimento degli assioni cui la probabilità deve obbedire.
Sia S un insieme di eventi (discreto o continuo) e ad ognuno di essi è possibile associare un numero
P, tra  ed 1, nel rispetto dei seguenti assiomi.
-
Non esistono valori negativi perché sarà sempre
P(A) 
-
Se un evento è certo sarà
P(A) = 1
-
Se un evento è impossibile sarà
P(A) = 
-
Se due o più eventi sono mutuamente esclusivi, sarà
P(AUB) = P(A) + P(B)
In coerenza con la definizione assiomatica della Probabilità è possibile associare ad essa altri due
concetti importanti :
-
La densità di probabilità
-
La funzione di distribuzione
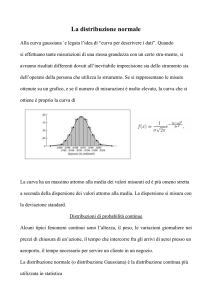
Infatti con riferimento alla fig. n. 1 in cui è rappresentata una funzione y=(x) nell’intervallo a, b, se
l’area contenuta tra la curva e l’intervallo è pari ad 1 la y=(x) sarà una curva di densità, infatti:
2
P   f ( x)  dx
fig.1
-
non esiste possibilità che si verifichi un evento al di fuori di a,b:
P() =
-
è certo che si possa verificare un evento in (a,b)
P(S) = 1
-
i valori di dP = f(x)  dx sono positivi sempre:
f(x)  
-
eventi mutuamente esclusivi determinano
P(x1+x2) = P(x1) + P(x2) = f1(dx1) + f2(dx2)
Pertanto la y= f(x) è una curva di densità di probabilità.
Se integro la y= f(x) in un intervallo (a,)

ottengo
F=

a
f ( x)dx
La F prende il nome di distribuzione di probabilità e risponde alla domanda “Qual è la probabilità
che si verifichi un evento tra a ed ” (fig. n.2)
3
Fig.2
Questa probabilità è rappresentata dall’area tratteggiata
E’ evidente che
F(x) =

b
a
f ( x)dx  1
fuori dall’intervallo sarà
F(x) = 
Pertanto mentre la densità di probabilità è riferita ad un punto sull’asse reale x, la funzione
distribuzione presume un intervallo.
2.2 Teoremi sulla probabilità
Vedremo meglio nel seguito che la v.c. “misura” si distribuisce secondo la legge di Gauss
rappresentata in figura
4
Per ora diremo soltanto che la curva è simmetrica rispetto ad un valore centrale  che è la media
delle misure e che, in un buon sistema di misure, la probabilità che si presentino valori molto
discosti dalla  è piccola, mentre la probabilità che si presentino valori prossimi alla  è più alta,
infatti 1 << 2
La densità di probabilità  è espressa dalla
f 
1
2  
e

( x )2
2 2
Pertanto se di una popolazione conoscessi a priori la media  e la varianza 2 potrei tracciare la
curva .
Supponiamo che la curva sia quella in fig.
Se volessi conoscere la probabilità che si presenti una misura tra i valori a e b, basterà conoscere
l’area compresa tra la curva e l’intervallo a,b.
2.3 Teorema della probabilità totale
5
Continuando ad utilizzare la curva di Gauss supponiamo di aver misurato l’angolo AôB con la
precisione del 1”
e che la curva teorica di distribuzione degli scarti (errori) sia quella in figura.
Se vogliamo conoscere la probabilità che si presenti un errore tra 2” e 3” (negativo), basta che
determini l’area A compresa tra la curva e l’intervallo richiesto.
Analogamente se voglio conoscere la probabilità tra 5” e 6” (positivo).
E’ chiaro che la probabilità che si presenti un errore tra 2” e 3” (negativo) o tra 5” e 6” sarà
P=A+B
Questa è l’espressione della probabilità totale nel caso che i sottoinsiemi di misure siano disgiunti:
Vediamo il caso in cui i due sottoinsiemi presentano un’intersezione:
6
AB
= (A-B)  B
P(AB) = P(A-B) + P(B)
P(A-B) = P(A) – P (AB)
P(AB) = P(A) + P(B) – P(AB)
P (0”  2”) = a + b
P(1” 3”) = b + c
P (1”  2”) = b
P (0”  3”) = (a + b) + (b + c) – b = a + b + c
2.3.1
La probabilità condizionata
In alcuni casi i valori argomentali possono essere classificati con due distribuzioni di probabilità
diverse, ed in questi casi è importante vedere se tra le due distribuzioni c’è o meno una
correlazione.
Vediamo di spiegarci con un esempio.
7
Supponiamo che di un fabbricato che si è instabilizzato sono stati tenuti in osservazione 100 punti,
nei quali si sono misurati al tempo t1 gli spostamenti  e rotazioni , riassunti nella tabella
seguente:

+
-
()
+
20
10
0.3
-
40
30
0.7
()
0.6
0.4
1

Da questo set di misure posso dire che:
1) La priorità con cui si presenta
P(+ +) = 0.20
P(+) = 0.3
P(+ -) = 0.10
P(-) = 0.7
P(- +) = 0.4
P(+) = 0.6
P(- -) = 0.3
P(-) = 0.4
e posso anche affermare che se si è verificata una + , la priorità con cui si presenta
+ = 20/60 = 1/3 = 0.333
- = 40/60= 2/3 = 0.666
Queste due valutazioni sono condizionate dal fatto che ho ristretto le priorità di  a quella di 
già verificatasi come positiva.
8
In coerenza all’esempio potremo scrivere
P (+ . +)
P (+ / +) = ------------
vale a dire
P(+ )
“La priorità con cui si può verificare uno spostamento (+) una volta che si è verificata una
rotazione (+) è data dalla priorità dell’insieme intersezione (+ , +) divisa per la priorità che si
verifichi una + nell’intera popolazione infatti:
20/100
P (+ / +) = ------------ = 20/60 = 1/3
60/100
Domandiamoci ora se tra gli eventi riportati in tabella vi sia un legame, notiamo infatti che
correlando la qualità di uno spostamento alla qualità di una rotazione il valore cambia rispetto a
quelli presi in assoluto.
Se però
P (A/B) = P (A)
vale a dire se la probabilità condizionata di A rispetto a B fosse sempre
uguale ad P (A), gli eventi A e B sarebbero indipendenti.
Supponiamo che la tabella precedente assumesse i valori seguenti:


+
-

+
20
20
0.4
-
30
30
0.6

0.5
0.5
1
Avremo che P(+ ) = 40/100 = 0.4
P(+ / +)
ma anche P (+ / +) = ------------ = 0.2/0.5 = 0.4
P(+)
9
quindi il fatto che si sia verificata una + non condiziona il risultato di +
il che significa che + è indipendente da +
2.3.2
La probabilità composta
Si definisce probabilità composta quella dell’evento che contemporaneamente appartiene a due
insiemi:
+
+
probabilità composta P(+ +)
Nel caso in cui gli eventi sono indipendenti
Sarà P(+ +) = P(+) x P(+)
Come è facile dimostrare, infatti se:
P(+ +)
P(+ / +) = --------------- = P(+)
P(+)
P (+ +) = P(+) x P(+)
10