Trigonometria - MATEMATICAeSCUOLA

Trigonometria
Area di un triangolo inscritto in un trapezio rettangolo
Problema
Si consideri un trapezio rettangolo ABCD, rettangolo in A e B, il cui lato obliquo CD di misura 2a forma con
la base maggiore AD un angolo di 60°.


1) Determinare le misure dei lati del trapezio sapendo che il perimetro è 2 p  5  3 a .
2) Fissare su AD un punto E ed indicare con F la sua proiezione ortogonale su CD. Indicata con  la
misura dell’angolo ABE, determinare la posizione del punto E in modo che l’area del triangolo BEF
sia
a2 3
.
2
Soluzione
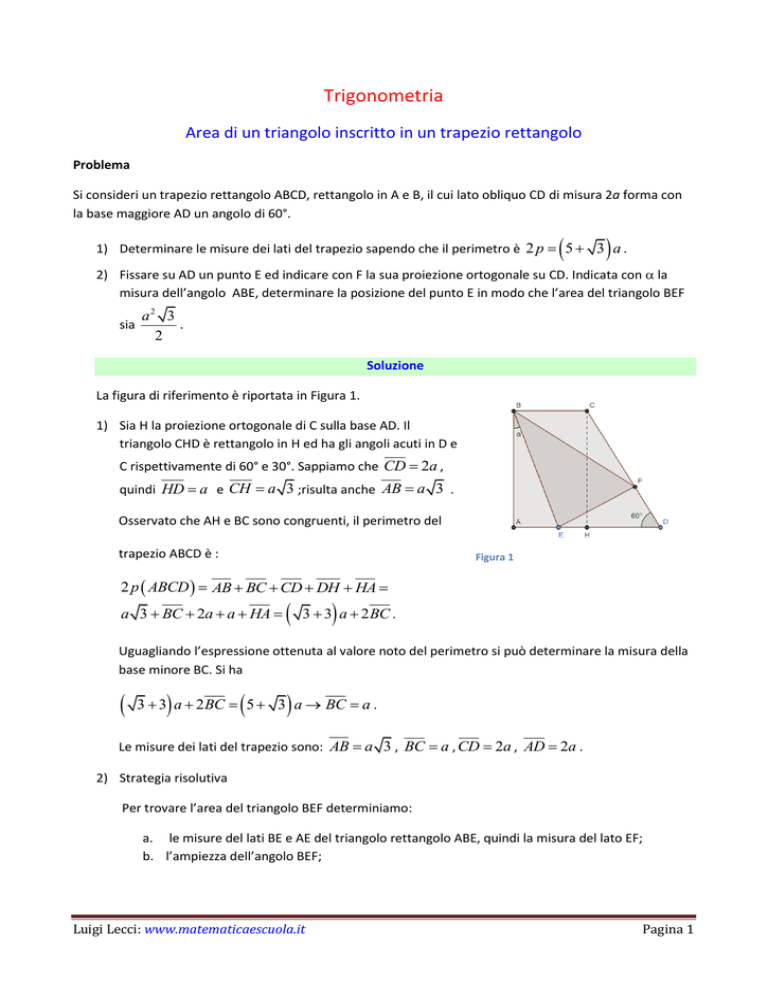
La figura di riferimento è riportata in Figura 1.
1) Sia H la proiezione ortogonale di C sulla base AD. Il
triangolo CHD è rettangolo in H ed ha gli angoli acuti in D e
C rispettivamente di 60° e 30°. Sappiamo che CD  2a ,
quindi HD  a e CH  a 3 ;risulta anche AB  a 3 .
Osservato che AH e BC sono congruenti, il perimetro del
trapezio ABCD è :
Figura 1
2 p  ABCD   AB  BC  CD  DH  HA 
a 3  BC  2a  a  HA 


3  3 a  2 BC .
Uguagliando l’espressione ottenuta al valore noto del perimetro si può determinare la misura della
base minore BC. Si ha




3  3 a  2BC  5  3 a  BC  a .
Le misure dei lati del trapezio sono: AB  a 3 , BC  a , CD  2a , AD  2a .
2) Strategia risolutiva
Per trovare l’area del triangolo BEF determiniamo:
a. le misure del lati BE e AE del triangolo rettangolo ABE, quindi la misura del lato EF;
b. l’ampiezza dell’angolo BEF;
Luigi Lecci: www.matematicaescuola.it
Pagina 1
ciò fatto si potrà calcolare l’area del triangolo BEF come il semiprodotto delle misure dei due lati BE,
EF per il seno dell’angolo compreso BEF(1).
Misura di BE e AE
BE 
AB
a 3
; AE  AB  tg  a 3  tg .

cos  cos 
Per differenza ricaviamo la misura di ED

ED  AD  AE  2a  a 3  tg  a 2  3tg

Dal triangolo rettangolo DEF, sapendo che l’angolo in D misura 60°, deduciamo:
EF 


3
ED
.
3  a 2  3tg 
2
2
Ampiezza dell’angolo BEF
L’angolo di AEB è 90°- ed inoltre è noto che quella di DEF è 30°, da ciò segue che


BEF  180  AEB  DEF  180   90    30   60  
Area del triangolo BEF
Area  BEF  


1 a 3
3
1
 a 2  3tg 
 sen  60    
 BE  EF  sen  60     
2 cos 
2
2
3a 2 
sen 
3a 2
sen
60

cos


cos
60

sen


 2  3

 2cos   3sen 



4cos2 
4cos  
cos  

 3

3a 2
1
 2 3 cos 2   cos  sen  3sen 2
cos   sen  

2
8cos

2
2



Uguagliamo il valore ottenuto per l’area al valore noto Area( BEF ) 


3a 2
a2 3
2
2

2
3
cos


cos

sen


3
sen


8cos 2 
2


a2 3

2
(*)
Osservazioni sulla variabilità di 
Al variare del punto E sulla base AD del trapezio l’ampiezza dell’angolo  varia dal valore =0°,
 AD 
 2 
  arctg 
 , corrispondente alla
 3
 AB 
corrispondente alla posizione EA, al valore arctg 
(1)
Per un noto teorema di trigonometria
Luigi Lecci: www.matematicaescuola.it
Pagina 2
posizione ED. Facciamo notare che con ED il triangolo BEF degenera nel doppio segmento BD e
quindi ha area nulla.
Semplificazione dell’equazione (*)
Per i valori che può assumere l’ampiezza di  risulta cos0 per cui, ritenendo a0, l’equazione
liberata dal denominatore, dopo alcune elaborazioni diventa
3sen2  3 cos  sen  2cos2   0 ,
e dividendo per cos 2  si passa all’equazione
3tg 2  3tg  2  0
L’equazione è soddisfatta per tg 
tg  
3
e
3
3
. Dei due valori ottenuti, tenendo conto
2
del dominio per , è accettabile solo il primo e
 3
 3   30 .


quindi deve risultare   arctg 
Figura 2
Il valore =30° corrisponde alla coincidenza di E con
H; la figura relativa è rappresentata in Figura 2.
Luigi Lecci: www.matematicaescuola.it
Pagina 3