Esercizio I
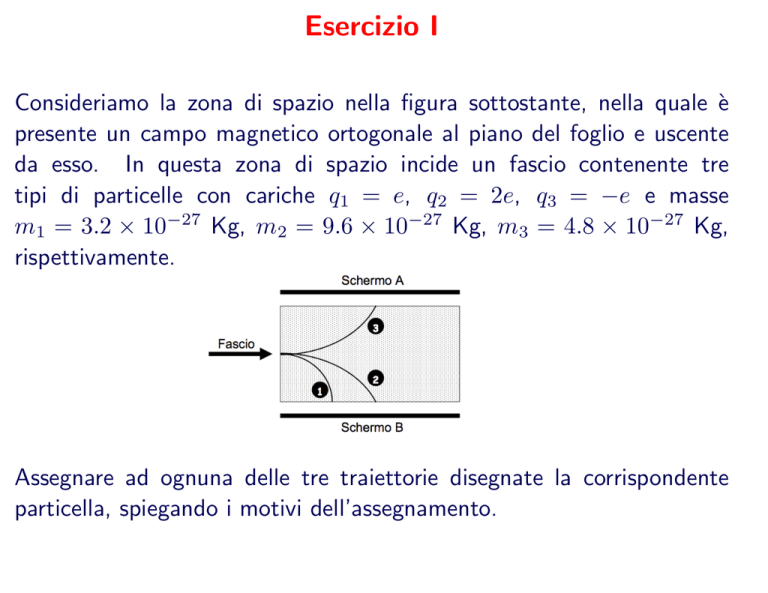
Consideriamo la zona di spazio nella figura sottostante, nella quale è
presente un campo magnetico ortogonale al piano del foglio e uscente
da esso. In questa zona di spazio incide un fascio contenente tre
tipi di particelle con cariche q1 = e, q2 = 2e, q3 = −e e masse
m1 = 3.2 × 10−27 Kg, m2 = 9.6 × 10−27 Kg, m3 = 4.8 × 10−27 Kg,
rispettivamente.
Assegnare ad ognuna delle tre traiettorie disegnate la corrispondente
particella, spiegando i motivi dell’assegnamento.
Esercizio I, soluzione
La particella 3 ha carica opposta a quella delle altre due, quindi non può che
corrispondere alla traiettoria 3, che “gira” in senso opposto alle altre due.
mv
Il raggio della traiettoria è proporzionale al rapporto massa/carica: r =
. Le
qB
particelle 2 e 3 hanno rapporto massa/carica uguale e opposto, minore (in valore
m3
m2
m1
assoluto) di quello per la particella 1: −
=
>
. Di conseguenza la
q3
q2
q1
traiettoria 2 (che ha lo stesso raggio di curvatura della traiettoria 3) corrisponde alla
particella 2, la traiettoria 1 (con raggio di curvatura minore) alla particella 1.
Esercizio II
Un protone avente un velocità di 8 × 106 m/s ha una traiettoria ad elica
caratterizzata da un passo identico al raggio. Per quale valore di campo
magnetico e quale direzione della velocità ciò è possibile?
Esercizio II, soluzione
Un protone avente un velocità di 8 × 106 m/s ha una traiettoria ad elica
caratterizzata da un passo identico al raggio. Per quale valore di campo
magnetico e quale direzione della velocità ciò è possibile?
Chiamiamo vk e v⊥ le velocità del protone parallele e perpendicolari al campo B. Nel
piano ortogonale a B, il protone esegue un moto circolare uniforme di raggio r sotto
2
mv⊥
mv⊥
l’azione della forza di Lorentz eBv⊥: vale eBv⊥ =
, ovvero r =
. Il periodo
r
eB
del moto è
2πr 2πm
=
.
T =
v⊥
eB
In tale periodo, il protone percorre lungo la direzione di B uno spazio d = T vk.
Uguagliando d e r, troviamo
2πmvk mv⊥
=
,
eB
eB
ovvero 2πvk = v⊥ . Notare come tale risultato non dipenda né dalla carica né dalla
massa della particella e neanche dal modulo del campo magnetico.
Esercizio III
Uno ione di massa sconosciuta m e di
carica q viene emesso in una regione S, con
velocità iniziale trascurabile, accelerato da una
differenza di potenziale V ed infine introdotto
in un campo magnetico B ortogonale alla sua
velocità.
Nel campo (che assumiamo costante) lo ione percorre una
semicirconferenza e va a colpire una lastra fotografica a distanza x
dalla fenditura d’ingresso.
B 2q 2
x .
• Dimostrare che la massa dello ione è data da m =
8V
• Determinare x per uno ione Na+ (di massa m = 38.16 × 10−27 kg)
accelerato da una differenza di potenziale di 1000 V in un campo
B = 0.5T.
Esercizio III, soluzione
• La particella di carica q attraversa una differenza di potenziale V e
quindi acquista un’energia cinetica mv 2/2 = qV . Una volta penetrata
nel campo magnetico con velocità v subisce una forza centripeta
f = qvB che causa una traiettoria semicircolare di raggio r, per la
quale vale la relazione mv 2/r = f . Da qui si ottiene v = qrB/m,
che sostituita nella prima eqauzione dà m(qrB/m)2/2 = qV , da cui
m = qr2B 2/2V = qx2B 2/8V giacché x = 2r.
p
• Dalla relazione prima dimostrata si ottiene x =
8mV /qB 2.
Sostituiendo i valori si trova x = 0.087 m, ovvero x = 8.7 cm.












