Tutoraggio di Elettricità e Magnetismo
- Soluzioni degli esercizi
Davide Vadacchino ([email protected])
Umberto Tamponi ([email protected])
28/29 Ottobre 2013
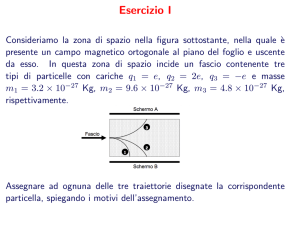
Esercizio 1
Osservando il circuito si nota che sono collegate direttamente al potenziale A le resistenze R1 ,R3 ,R4 ed R6 . il circuito puo’ quindi essere ridisegnato ponendo tre blocchi
di resistenze in parallelo tra i potenziali A e B: il primo blocco, α, consiste nelle resistenze R1 ed R2 messe in serie, il blocco β nella serie tra R5 e il parallelo R4 -R6 , ed
infine il blocco γ ećostituito dalla sola resistenza R3 .
Le resistenze equivalenti di ciascuna porzione sono:
Rα = R1 + R2 = 80Ω
Rβ = (1/R4 + 1/R6 )−1 + R5 = 25Ω
Rγ = R3 = 50Ω
La resistenza totale sará quindi data da:
Rtot = (1/Rα + 1/Rβ + 1/Rγ )−1 = 13.8Ω
Esercizio 2
Una carica q in moto in un campo magnetico risente della forza di Lorentz. In questo
caso, essendo la velocitá e il campo magnetico ortogonali, la sua espressione é F~l =
~ · u~z , dove u~z é il versore del piano su cui giacciono ~v e vecB. Essendo per
q|~v ||B|
costruzione sempre ortogonale alla velocitá, la forza di Lotenz non compie lavoro e si
limita a curvare la traiettoria della paticella rendendola circolare. Si possono quindi
1
applicare le leggi del moto circolare imponendo che la forza di Lorentz giochi il ruolo
della forza centripeta:
v2
Fl
q
ac =
=
= vB
R
m
m
da cui si ricava il raggio di curvatura
v m
R=
.
B q
Data la geometria del problema il punto di impatto si troverá ad una distanza pari a
2R dal punto di immissione e, nota la velocitá dell particelle, la sua misura permette
di ricavare il rapporto carica/massa di ciascuna particella.
Un apparato strutturato come descritto nel problema prende il nome di spettrometro
di massa.
Esercizio 3
Le particelle cariche risentiranno della forza elettrica Fe e della forza di Lorentz Fl .
Le particelle che attraversano inidisturbate l’apparato devono subire una forza totale
nulla, per cui Fe ed Fl devono essere parallele ed entrambe ortogonali alla velocita’.
Tale richiesta corrisponde alla richiesta di mutua ortogonalitá tra campo elettrico,
campo magnetico e velocitá. La condizione di equilibrio per una particella con carica
q e velocitá v sará:
E
Fl = Fe → qvB = qE → v = .
B
Esercizio 4
Il campo magnetico esterno agirá sulla corrente di elettroni in moto nella sbarretta
curvandone la traiettoria. A seguito di questo effetto si ha un accumulo di cariche
negative su una delle superfici laterali e si instaurerá di conseguenza una differenza di
potenziale VH tra tale superficie e quella a lei opposta.
La forza di Lorentz percepita da un elettrone sará
eiB
iB
=
nea2
na2
dove la velocitá di deriva vd degli elettroni che fluiscono con corrente i é stata scritta
i
2
come vd = nea
2 , essendo n il numero di elettroni di conduzione e a la sezione trasvesra
del conduttore.
Man mano che le cariche si accumulano sulla faccia del conduttore, la tensione VH
crescerá opponendosi all’accumulo di ulteriori cariche, sino a che non si raggiunge
una situazione di equilibrio in cui la differenza di potenziale compensa completamente
l’effetto delal forza di Lorentz.
Assumendo che il campo elettrico dovuto a VH sia uniforme si potrá scrivere, all’equilibrio:
Fl = evd B =
Fl = Fe →
iB
− eE = 0
na2
2
da cui, ponendo E = aVH , si otterrá
VH =
iB
.
nea
Esercizio 5
Una carica in moto si comporta a tutti gli effetti come una corrente elettrica. Nel caso
specifico la carica q percorre l’intera circonferenza in un tempo pari al suo periodo di
q
qω
qv
rotazione T = 2π
ω , per cui la corrente corrispondente sará i = T = 2π = 2πR , dove R
é il raggio della circonferenza e v la velocitá della carica.
Il problema si riconduce quindi al calcolo del campo magnetico generato da una spira
circolare percorsa da una corrente i, che puo’ essere affrontato utilizzando il principio
di sovrapposizione:
Z
Z
µ0 i d~l × ~ur
B = dB =
.
4π r2
Restringendo il calcolo all’asse della spira (definito come asse z del problema), si
nota che per ragioni di simmetria il campo deve essere diretto lungo z. Il calcolo
2
0 iR
dell’integrale, svolto su tutti i manuali di fisica II, porta all’espressione B(z) = µ2z
3
che nel caso specifico diventa
µ0 qvR
B(z) =
.
4πz 3
Esercizio 6
La forza di Lorentz e’sempre ortogonale al campo magnetico, per cui, definendo z
l’asse di simmetria del rivelatore (asse orizzontale nella figura), sará sempre diretta
nel piano xy. La traiettoria delle particelle, proiettata su tale piano, sará quindi una
circonferenza. La componente lunzo z della velocitá peró, essendo parallela al campo
~ non risentirá di alcun effetto. Il moto complessivo sará uindi dovuto alla somma di
B,
un moto rettilineo uniforme lungo z ed un moto circolare uniforme nel piano xy, dando
cosi’ orgine ad una traiettoria spiraleggiante, con asse parallelo al campo magnetico.
La direzione di avvitamento della spirale permette infine di determinare il segno della
carica della particella.
Il raggio di curvatura é determinato esclusivamente dalla componente della velocita’
ortogonale al campo magnetico, definita come vt = v sin θ avendo chiamato θ l’angolo
tra ~v e l’asse z, per cui, in base a quanto ricavato nell’esercizio 2:
R=
vm sin θ
vt m
=R=
Bq
Bq
pt
tm
= R = Bq
, dove
Introducendo il momento della particella p = mv si ha R = vBq
pt = p sin θ é comunemente detto impulso trasverso (rispetto all’asse z del rivelatore)
della particella. Si noti come tale misura non richieda di conoscere la massa della
particella ma solo la sua carica, che deve essere assunta come postulato per la misura
3
del momento. Per determinare la risoluzione sul momento trasverso si applicano le
regole di propagazione degli errori, assumendo che il campo magnetico sia noto con un
errore trascurabile:
δpt
δR
= Bq
pt
R
Campi magnetici piccolo permettono quindi tracciature piu’ precise, ma richiedono
ovviamente volumi di tracciamento maggiori, che possono essere sperimentalemnte
problematici da costruire.
Esercizio 7
Durante il processo di carica si potra’ scrivere il bilancio della cadute di potenziale
come
V − VC = VR
dove VR (t) = Ri(t) = R dQ(t)
e VC (t) =
dt
Q(t)
C .
dt =
Esplicitando dt si ottiene
RC · dQ
VC −Q
effettuando il cambio d variabile V C − Q = x, dQ = −dx l’integrazione diviene piú
semplice:
t
dx
dt = −RC
→ x(t) = x(0)e− RC
x
Sostituendo l’espressione originale di x si ottiene
t
Q(t) = V C(1 − e− RC ).
Durante il processo di scarica la somma delle cadute di potenziale sul condensatore
VC e sulla resistenza VR devono compensarsi, per cui
VC (t) = −VR (t).
e VC (t) =
D’altro canto VR (t) = Ri(t) = R dQ(t)
dt
Q(t)
C ,
per cui l’equazione diviene
Q(t)
dQ(t)
dQ(t)
dt
= −R
→
=−
C
dt
Q(t)
RC
Integrando l’espressione si ottiene
t
Q(t) = Q(0)e− RC
per cui la carica si dimezzera dopo un tempo t1/2 = −RCln(0.5).
4