21 Dicembre - Sezione di Fisica

Corso di Chimica e Fisica Generali per Biotecnologie
Esame scritto, modulo di Fisica 1 – 21 Dicembre 2012
Il tempo a disposizione è di tre ore. E’ ammesso l’uso di calcolatrici. Non è ammesso l’uso di appunti, libri, computer,
telefoni, altri dispositivi di comunicazione. Un libro di testo è a disposizione per consultazione. Costanti utili:
accelerazione di gravità g = 9.81 m/s2 ; massa dell’elettrone me = 9.10×10−31 kg; carica dell’elettrone e = 1.602×10−19
C; permeabilità dielettrica del vuoto 0 = 8.85 × 10−12 C2 /(Nm2 ). Si raccomanda di spiegare in modo conciso ma
chiaro il procedimento seguito.
Problema 1 (10 punti)
Un corpo si trova ad un estremo di un asse lungo L = 2 m, che viene gradualmente inclinato partendo dalla posizione
orizzontale. Il corpo inizia a muoversi quando l’angolo di inclinazione raggiunge θ = 30◦ . Da questo punto l’angolo di
inclinazione resta costante. Determinare:
a) il coefficiente di attrito statico µs tra il corpo e lasse;
b) il coefficiente di attrito dinamico µd sapendo che la velocità con cui arriva al suolo vale v = 3 m/s.
Problema 2 (10 punti)
Due pendoli si trovano fermi nella situazione illustrata in figura. Il primo viene lasciato libero
alla quota h e colpisce il secondo. Supponendo che l’urto sia completamente anelastico e
trascurando tutti gli attriti e le masse dei fili, qual è l’altezza massima h0 alla quale risalgono
le due sfere attaccate?
Problema 3 (6 punti)
Due fogli di alluminio distanti 0.5 mm costituiscono un condensatore piano di capacità pari a C = 7 × 10−12 F. Si
trovi l’area dei fogli (nell’approssimazione di condensatore piano infinito) e l’intensità del campo elettrico quando il
condensatore viene collegato ad una pila da 16 V.
Problema 4 (6 punti)
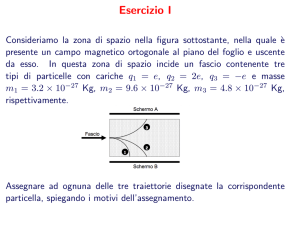
Consideriamo la zona di spazio nella figura sottostante, nella quale è presente un campo magnetico ortogonale al piano
del foglio e uscente da esso. In questa zona di spazio incide un fascio contenente tre tipi di particelle con cariche
q1 = e, q2 = 2e, q3 = −e e masse m1 = 3.2 × 10−27 kg, m2 = 9.6 × 10−27 kg, m3 = 4.8 × 10−27 kg, rispettivamente.
Assegnare ad ognuna delle tre traiettorie disegnate la corrispondente particella, spiegando i motivi dell’assegnamento.
1
Soluzione
Problema 1 Sulla massa ferma agiscono una forza di reazione vincolare N che compensa la componente M g cos θ
della forza peso normale al piano; una componente della forza peso M g sin θ compensata dalla forza di attrito statico
f ≤ µs N = µs M g cos θ. La massa inizia a muoversi quando M g sin θ = µs M g cos θ, ovvero µs = tan θ = 0.577.
Nella caduta la forza di attrito dinamico fa un lavoro W = −µd M g cos θL sulla particella. Per il teorema dell’energia
cinetica, Ef −Ei = W , dove E = Ek +U è l’energia meccanica: Ei = mgL sin θ quando la massa comincia a muoversi,
Ef = mv 2 /2 quando tocca terra. da qui: mv 2 /2 − mgL sin θ = −µd mgL cos θ, ovvero µd = tan θ − v 2 /(2gL cos θ) =
0.577 − 9/(2 · 9.81 · 2 · 0.866) = 0.312.
Problema 2 Scomponiamo il moto in tre parti.
√
Parte prima: la pallina m1 arriva nel punto più basso con velocità orizzontale v1 = 2gh (conservazione dell’energia).
Parte seconda: urto anelastico in cui le palline si fondono. Per la conservazione
della quantità di moto, la velocità V
√
delle palline fuse dopo l’urto è data da (m1 + m2 )V = m1 v, ovvero V = m1 2gh/(m1 + m2 ).
Parte terza: le palline risalgono fino alla quota h0 = V 2 /2g (di nuovo, conservazione dell’energia) ovvero:
2
m1
0
h. Notare che l’energia NON si conserva nell’urto anelastico, quindi NON si può usare la conserh =
m1 + m2
vazione dell’energia per l’intero moto.
Problema 3
Per un condensatore piano, C = 0 A/d, quindi A = Cd/0 = 7 × 10−12 · 0.5 × 10−3 /(8.85 × 10− −12) m2 , cioè
A = 3.95 × 10−4 m2 =3.95 cm2 .
Il campo eletrico è semplicemente dato dalla relazione V = Ed, da cui E = V /d = 16/(0.5 × 10−3 ) V/m = 3.2 × 104
V/m.
Problema 4
La particella 3 ha carica opposta a quella delle altre due, quindi non può che corrispondere alla traiettoria 3, che “gira”
in senso opposto alle altre due.
mv
Il raggio della traiettoria è proporzionale al rapporto massa/carica: r =
. Le particelle 2 e 3 hanno rapporto
qB
m3
m2
m1
massa/carica uguale e opposto, minore (in valore assoluto) di quello per la particella 1: −
=
>
. Di
q3
q2
q1
conseguenza la traiettoria 2 (che ha lo stesso raggio di curvatura della traiettoria 3) corrisponde alla particella 2, la
traiettoria 1 (con raggio di curvatura minore) alla particella 1.
2