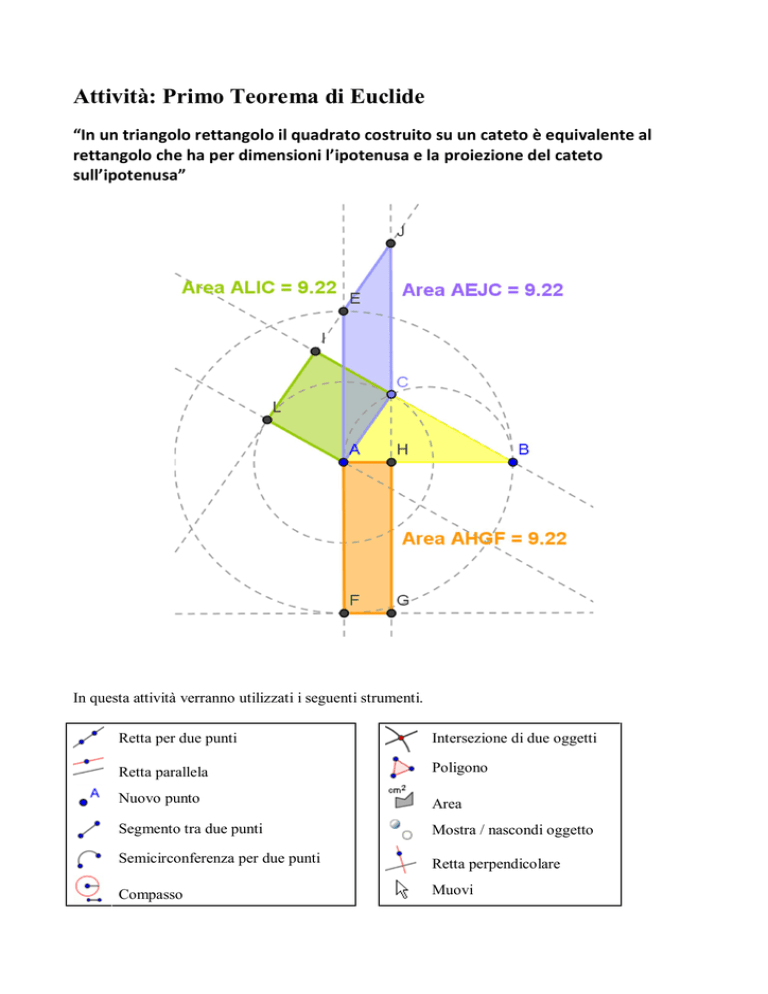
Attività: Primo Teorema di Euclide
“In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al
rettangolo che ha per dimensioni l’ipotenusa e la proiezione del cateto
sull’ipotenusa”
In questa attività verranno utilizzati i seguenti strumenti.
Retta per due punti
Intersezione di due oggetti
Retta parallela
Poligono
Nuovo punto
Area
Segmento tra due punti
Mostra / nascondi oggetto
Semicirconferenza per due punti
Retta perpendicolare
Compasso
Muovi
Processo di costruzione
1.
2.
3.
4.
Tracciare il segmento AB tra i punti A e B
Costruire la semicirconferenza di diametro AB
Fissare un punto C sulla semicirconferenza
Costruire il triangolo ABC. Misura l’angolo in C. Fai il test di trascinamento per verificare
che il triangolo sia rettangolo in C.1
5. Costruire le perpendicolari al diametro AB condotte da C e da A
6. Determinare il punto D di intersezione tra la perpendicolare e il diametro
7. Costruire sulla perpendicolare per A nel semipiano che non contiene C un segmento AF
congruente ad AB
8. Costruire il rettangolo di lati AH e AF
9. Costruire il quadrato ACLI di lato il cateto AC
10. Chiama E il punto di intersezione tre la retta LI e la retta AF
11. Verifica che AE è congruente a AF 2
12. Costruisci il parallelogramma EACJ
13. Eseguire il test di trascinamento per verificare se la costruzione è corretta
14. Utilizzare lo strumento area per calcolare l’area dei tre parallelogrammi
1
Perché questo triangolo sarà sicuramente rettangolo?
2
Dimostra su un foglio di carta che il triangolo LEA è congruente al triangolo ABC












