LE GEOMETRIE NON EUCLIDEE

LE GEOMETRIE NON EUCLIDEE
APPARENTI ASSURDITÀ
Alunni: Valentina Giovinco, Valentina Polverazzi, Ilenia Prezioso,
Jacqueline Spera (Classe V B, a. s. 2012 – 2013, Liceo Scientifico “Enzo
Siciliano”, Bisignano CS.
Referente: Prof.ssa Franca Tortorella
1
Un salto nel passato per conoscere il mondo della geometria.
Curiosità ed esigenze pratiche hanno da sempre spinto l’uomo ad indagare e ad
analizzare il mondo circostante.
Le prime figure geometriche furono, probabilmente, il
risultato umano di riportare su una superficie piana la
forma del Sole, della Luna, degli animali o, forse, dell’uomo
stesso. La natura sembra infatti divertirsi nel mostrare sé
stessa tramite elementi che rappresentano dei veri e
proprio capolavori geometrici.
Le piramidi, i templi, la necessità di ricalcolare i confini dei terreni che le inondazioni
del Nilo periodicamente cancellavano provano che già nella civiltà egizia vi fosse un
certo grado di conoscenza geometrica, anche se bisognerà attendere fino al VII
secolo a.C. per assistere ad uno sviluppo maggiore, proveniente in gran parte dagli
studi condotti in Oriente, che menti eccelse dalla parte opposta del mondo
rielaborarono in maniera più formale.
2
Ufficialmente la geometria nasce nella civiltà greca con Talete, nel
VI secolo a.C.
Fra gli studiosi della Magna Grecia si distinse
Pitagora, il quale, attorno al VI a.C., con la
fondazione della Scuola Pitagorica a Crotone,
Talete
diede un grande apporto a questa disciplina.
Viene infatti attributo a lui quello che oggi conosciamo con il
nome di teorema di Pitagora, che stabilisce una relazione
fondamentale tra i lati del triangolo.
Pitagora
Fu tuttavia Euclide, nel III secolo, ad ottenere il primato tra i protagonisti della storia
della matematica; primato che riuscì a mantenere per secoli dopo la sua morte.
L’opera che gli conferì tale immortalità fu la raccolta dei 13
libri degli Elementi, in cui il matematico greco riunì, in
maniera sistematica e dettagliata, tutto il sapere geometrico
dei sui tempi.
Euclide
I primi sei tomi trattano la geometria piana, i quattro
seguenti i rapporti tra le grandezze, mentre gli ultimi tre
riguardano la geometria
solida.
Per anni l’opera di Euclide fece da base a nuovi
studi per il perfezionamento della geometria.
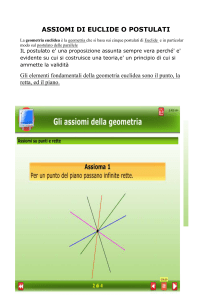
Nel primo libro degli “Elementi”, Euclide tratta degli
enti fondamentali della geometria (punto, retta e
piano) attraverso cinque assiomi e cinque postulati.
La differenza tra postulati e assiomi consiste nel fatto
che gli assiomi sono nozioni comuni che non si
riferiscono direttamente alla geometria, mentre i
postulati sono ragionamenti basati sugli enti
fondamentali.
3
Assiomi:
1.Cose uguali ad una stessa cosa sono uguali tra loro;
2.Aggiungendo (quantità) uguali a (quantità) uguali le somme sono uguali;
3.Sottraendo (quantità) uguali da (quantità) uguali i resti sono uguali;
4.Cose che coincidono con un'altra sono uguali all'altra;
5.L'intero è maggiore della parte.
Postulati:
1 .Un segmento di linea retta può essere disegnato unendo due punti a caso;
2. Un segmento di linea retta può essere esteso indefinitamente in una linea retta;
3. Dato un segmento di linea retta, un cerchio può essere disegnato usando il
segmento come raggio ed uno dei suoi estremi come centro;
4. Tutti gli angoli retti sono congruenti tra loro;
5. Se due rette tagliate da una trasversale formano angoli coniugati interni la cui
somma è minore di un angolo piatto,
allora le due rette si incontrano.
Il V postulato di Euclide.
Per secoli i matematici di tutto il mondo tentarono di dimostrare il V postulato.
4
L’esperienza di Posidonio
Posidonio (I secolo a.C.) propose una nuova definizione di rette
parallele: Due rette complanari sono parallele se sono
equidistanti.
Tale definizione sollevò tuttavia il problema dell’esistenza di rette
complanari ed equidistanti. Se, infatti, è facilmente dimostrabile
che due rette equidistanti non si incontrano, non si può provare
che due rette che non si incontrano sono equidistanti senza ricorrere al V postulato
di Euclide.
Giovanni Alfonso Borelli
Borelli (1608 – 1679) cercò di dimostrare l’esistenza di tali rette
attraverso il seguente postulato : Il luogo dei punti del piano
equidistanti da una retta e giacente dalla stessa banda di essa, è una
retta.
Proclo
Proclo (412 – 485) ritenne di poter sostituire il V postulato di
Euclide con uno logicamente equivalente o più restrittivo :
Se una retta incontra una di due rette parallele, incontra anche
l'altra.
Due rette parallele ad una terza sono parallele tra di loro.
Nasir – Eddin
Nella stessa direzione si mosse Nasir – Eddin (1201 – 1274),
il quale formulò il seguente postulato: Se due rette a,b sono
perpendicolari ed una obliqua ad una trasversale,
rispettivamente in A, B, i segmenti di perpendicolari
abbassati dai punti di b su a sono minori di AB, dalla parte di
AB da cui questa forma con b un angolo acuto.
Tali ipotesi non possono però essere dimostrate senza ammettere il postulato delle
parallele.
5
Il quadrilatero di Saccheri
Tra i tentativi di dimostrare il V postulato di Euclide un posto di rilievo dal
matematico gesuita Padre Giovanni Girolamo Saccheri (1667 – 1733).
Saccheri cominciò con l’osservare che attraverso la proposizione seguente è
possibile dedurre il V postulato:
Sia un segmento AB; dagli estremi si elevino due segmenti perpendicolari di uguale
grandezza tra loro, AC e BD; si congiunga C con D. Gli angoli α e β sono uguali e retti;
si verifica facilmente che anche gli angoli γ e δ saranno anch’essi uguali tra loro. Ma
tali angoli saranno anche retti? Secondo Euclide gli angoli γ e δ sono retti.
C
D
γ
A
δ
α
β
B
Saccheri vuole dimostrare la sua proposizione per assurdo, ovvero negando la tesi da
provare.
Egli è considerato il padre, seppure inconsapevole, delle geometrie non euclidee.
6
La geometria di Riemann
Negando il V postulato euclideo si può ammettere che per un punto esterno ad una
retta passino, nel piano, almeno due rette che non la incontrano, ma anche che per
il punto non passi alcuna retta che non incontra la retta data.
La prima ipotesi porta a sviluppare la geometria iperbolica, la seconda introduce un
sistema in cui non esistono rette parallele: la geometria introdotta da Riemann.
Pensiamo di sostituire l'assioma della parallela così formulato da Hilbert
data una retta r ed un punto A fuori di essa, allora nel piano individuato da r e da A
esiste al più una retta passante per A e parallela ad r
con una nuova proposizione che chiamiamo l'assioma di Riemann:
“Due rette qualsiasi di un piano hanno sempre almeno un punto in comune”
Da questo assioma segue immediatamente che non esistono rette parallele, per cui
non valgono più né il V postulato euclideo, né le proposizioni ad esso equivalenti.
Il sistema della geometria di Riemann si basa sull’ipotesi che lo spazio sia finito, in
particolare ciò fa riferimento alla retta che, a differenza dei casi euclideo e
iperbolico, si comporta come una linea chiusa, avente cioè lunghezza finita pur
essendo illimitata (si può continuare a percorrerla senza mai fermarsi).
Per assumere l’assioma di Riemann al posto di quello della parallela occorre
apportare ulteriori modifiche al sistema di assiomi della geometria euclidea, in
modo
da
non
cadere
in
un’incoerenza
del
sistema
stesso.
Geometria sferica e geometria ellittica
Da questo assioma segue immediatamente che non esistono rette parallele, per cui
non valgono più né il V postulato euclideo, né le proposizioni ad esso equivalenti.
Il sistema della geometria di Riemann si basa sull'ipotesi che lo spazio sia finito, in
particolare ciò fa riferimento alla retta che, a differenza dei casi euclideo e
iperbolico, si comporta come una linea chiusa, avente cioè lunghezza finita pur
essendo illimitata (si può continuare a percorrerla senza mai fermarsi).
Per assumere l'assioma di Riemann al posto di quello della parallela occorre
apportare ulteriori modifiche al sistema di assiomi della geometria euclidea, in
modo
da
non
cadere
in
un'incoerenza
del
sistema
stesso.
Geometria
sferica
e
geometria
ellittica
Dall'introduzione dell'assioma di Riemann si possono ottenere, a seconda delle
modifiche apportate agli assiomi, due geometrie: una detta sferica ed una detta
7
ellittica.
Partendo dall' ipotesi che due rette in un piano hanno sempre almeno un punto in
comune e che quindi in un piano non si può condurre (nel senso euclideo del
termine) una retta parallela ad un'altra, per un punto ad essa esterno, si può
arrivare a dimostrare che tutte le perpendicolari ad una retta r da una stessa parte
di essa, passano per un punto P, equidistante da ogni punto di r. Se immaginiamo,
poi, tutte le rette della parte opposta, possiamo notare che queste si incontrano
tutte in un punto P', con le stesse caratteristiche di P.
Al problema di sapere se P ed P' coincidono possiamo dare due risposte:
- P ed P' non coincidono, ma sono due punti distinti: due rette hanno perciò sempre
due punti in comune e si intersecano in una coppia di punti distinti: questo sistema
viene chiamato Geometria sferica, ed è assimilabile alla geometria euclidea della
sfera se per "rette" assumiamo le circonferenze massime;
- P ed P' coincidono: due rette si incontrano in un solo punto e due punti distinti
individuano una sola retta: questo secondo sistema viene chiamato Geometria
ellittica.
C'è uno stretto legame fra le due, e se ci si limita a considerazioni di carattere locale
le due teorie coincidono.
Descrizione delle caratteristiche principali della geometria sferica. Pensiamo di
dividere l'insieme dei punti del piano in coppie di punti, tali che ogni punto
appartiene ad una sola coppia e i punti di ciascuna coppia sono distinti. Per due
punti appartenenti a coppie distinte passa una sola retta, mentre per i due punti di
una stessa coppia passano più rette. Definiamo antipodali due punti appartenenti ad
una stessa coppia. In questa geometria le rette sono linee chiuse, due punti
antipodali dividono la retta in due parti congruenti, e tutte le rette che passano per
un punto dato passano anche per il suo antipodale.
Vediamo alcune delle principali caratteristiche di questa geometria:
- le rette sono linee chiuse;
- due punti antipodali dividono una retta passante per essi in due parti congruenti;
- tutte le rette sono congruenti, hanno tutte la stessa lunghezza (finita);
- per due punti passa almeno una retta, per coppie di punti antipodali ce ne possono
8
essere infinite;
- tutte le rette che passano per un punto dato passano anche per il suo antipodale;
- la somma degli angoli di un triangolo è maggiore di 180°, essa tende a 180° à
quando l'area del triangolo tende a 0. Parleremo in questo caso di eccesso angolare
(in contrapposizione al difetto angolare della geometria iperbolica), che sarà dato
da a+b+g-180°;
-non esistono triangoli o poligoni simili con aree
differenti;
-due rette perpendicolari alla stessa retta si
intersecano; tutte le perpendicolari alla stessa retta
passano
per
due
punti
antipodali;
-due rette qualsiasi hanno un unica perpendicolare in
comune;
-non
esistono
rettangoli;
- il teorema di Pitagora non vale, ma si avvicina al vero col tendere a zero dell'area
del triangolo.
Il modello sferico
La geometria sferica possiede un'immediata interpretazione nella geometria, questo
è il motivo per cui è stata privilegiata in questa trattazione, essa infatti si presenta
come un sistema geometrico che "descrive" la geometria di una superficie sferica
dello spazio euclideo; la seguente tabella fornisce la "traduzione" dei termini della
geometria sferica in quelli del suo modello euclideo.
Piano
Punto
Retta
Appartenenza
Punti antipodali
Insieme di punti di una superficie
sferica dello spazio euclideo
Punto della superficie sferica
Cerchio massimo della superficie sferica
(si ottiene intersecando la superficie
sferica con un qualsiasi piano passante
per il centro della sfera)
Usuale appartenenza in senso euclideo
Punti diametralmente opposti della
superficie sferica
9
Congruenza fra segmenti
Angolo tra due rette
Congrunza tra angoli
Congruenza fra gli archi di cerchio
massimo in geometria euclidea
Angolo diedro tra i due piani che
tagliano la sfera secondo le due rette,
oppure
angolo che coincide con l'angolo delle
due rette tangenti alla sfera nel punto
di intersezione delle due rette e giacenti
nei piani da esse individuati
Congruenza tra angoli in senso euclideo
In base a queste considerazioni è abbastanza intuitivo vedere che tutti gli assiomi
della geometria sferica risultano essere proposizioni valide in geometria euclidea.
Per
due
punti
antipodali
passano
infinite
rette,
infatti ogni piano passante per la retta che unisce i punti diametralmente opposti
della sfera la taglia secondo un cerchio massimo passante per i due punti (basti
pensare alla superficie terrestre e ai due poli, tutti i meridiani passano per essi);
Per
due
punti
non
antipodali
passa
una
sola
retta,
infatti i due punti sulla sfera individuano col centro di essa un unico piano che taglia
sulla sfera un cerchio massimo passante per i due punti.
Anche l'assioma di Riemann è verificato, infatti due rette si incontrano sempre,
poichè due cerchi massimi sono individuati da due piani, entrambi passanti per il
centro della sfera, che hanno quindi come intersezione una retta che taglia la sfera
in due punti antipodali comuni alle due rette.
- Tutte le rette sono congruenti, infatti tutti i cerchi massimi sono congruenti fra
loro.
- Tutte le perpendicolari alla stessa retta passano per due punti antipodali,
infatti tutti i cerchi massimi perpendicolari ad un dato cerchio massimo si incontrano
in due punti antipodali.
- Tutte le rette che passano per un punto dato passano anche per il suo antipodale,
infatti ogni cerchio massimo che passa per un punto passa anche per il suo
antipodale.
E così via; l'immediata visualizzazione della geometria sferica mediante questa
interpretazione consente di coglierne facilmente gli aspetti più caratteristici.
10
Le principali caratteristiche non euclidee della geometria sulla sfera
Aiutandoci sempre con il modello sferico, immaginando dunque che il nostro
ambiente geometrico non sia più il piano euclideo ma la superficie sferica S2,
riesaminiamo rapidamente le principali caratteristiche non euclidee di questa nuova
geometria.
Teniamo presente che il piano e la superficie sferica sono ambienti bidimensionali,
anche se la sfera in sé è un oggetto
tridimensionale.
- Le linee "rette" sulla superficie
sferica sono le circonferenze
massime, infatti, esse ci forniscono il
percorso più breve tra due punti,
non antipodali, di S2. (L'analogia tra
le rette del piano euclideo e le rette
della superficie sferica è molto forte:
entrambe sono caratterizzate dal
fatto di essere le linee più brevi,
l'unica differenza è che per punti
antipodali si perde l'unicità del
percorso minimo);
- Per due punti del piano euclideo
passa una e una sola retta, lo stesso accade per due punti non antipodali di S2, ma
per
due
punti
antipodali
passano
infinite
rette;
- due rette euclidee hanno al più un punto in comune mentre due rette di S2 hanno
sempre
due
punti
in
comune;
- nel piano euclideo esistono rette parallele, mentre non esistono rette parallele
(cioè rette che non si intersechino) in S2, ad esempio tutte le rette perpendicolari ad
una retta data, che nel piano euclideo sono tutte parallele tra loro, in S2 si
intersecano in una coppia di punti antipodali, detti in questo caso poli;
- nel piano euclideo esiste una e una sola retta passante per un dato punto P e
perpendicolare a una data retta, in S2 ciò è vero se e solo se P non è un polo per la
retta;
- le rette euclidee sono tutte infinitamente estese, mentre in S2 hanno tutte la
stessa
lunghezza
finita;
- il piano euclideo è infinitamente esteso, mentre S2 ha area finita;
- di tre punti qualsiasi di una retta euclidea, uno e uno solo sta tra gli altri due, la
stessa cosa non si può dire per una retta di S2 trattandosi di una linea chiusa, quindi
se due punti nel piano euclideo individuano un unico segmento, in S2 due punti
individuano
due
segmenti;
- altra differenza con la geometria euclidea è il fatto che la somma degli angoli di un
triangolo in S2 è maggiore di due angoli retti.
11
In figura è rappresentato il modello della geometria sferica, in cui il piano è
rappresentato dalle coppie di punti antipodali, e dalle rette che sono i cerchi
massimi. L'immagine mostra un triangolo con le tre altezze che si incontrano nei
poli; misurando gli angoli del triangolo si trova che la loro somma è maggiore di
180°.
La geometria ellittica e la fisica moderna
A partire dalla pubblicazione del saggio di Riemann, vennero intraprese diverse
ricerche nel campo della matematica pura e della fisica matematica che fanno uso
del concetto di varietà. In particolare, si indagò sulla possibilità di estendere alcune
discipline classiche della fisica matematica agli spazi a curvatura non nulla, nella
speranza di trovare nuove soluzioni ai problemi rimasti irrisolti. La condizione
indispensabile per queste ricerche era la necessità di esprimere le equazioni
fondamentali della fisica matematica in una notazione generale che restasse valida
per ogni tipo di spazio, euclideo e non. Da queste ricerche nasceva la nozione di
tensore e di calcolo tensoriale elaborata da Ricci-Curbastro e Levi-Civita verso la fine
del secolo. Intorno al 1912, Einstein si servì degli strumenti matematici elaborati da
Gauss, Riemann, Levi-Civita e Ricci-Curbastro per elaborare la teoria della relatività
generale. Nella conferenza di Kyoto del 1922, Einstein affermò
Se tutti i sistemi sono equivalenti allora la
geometria euclidea non può valere in ciascuno di
essi. Abbandonare la geometria e conservare le
leggi fisiche è come descrivere i pensieri senza
parole. Bisogna cercare le parole prima di poter
esprimere i pensieri. Che cosa si doveva cercare a
questo punto? Tale problema rimase insolubile per
me fino al 1912, quando all'improvviso mi resi
conto che la teoria di Gauss delle superfici forniva
la chiave per svelare questo mistero. Compresi che
le coordinate di una superficie di Gauss avevano un
profondo significato. Non sapevo però a
quell'epoca che Riemann aveva studiato i
fondamenti della geometria in maniera ancora più
profonda. [...] Mi resi conto che i fondamenti della
geometria avevano un significato fisico. Quando da
Praga tornai a Zurigo, vi trovai il matematico
Grossmann, mio caro amico: da lui appresi le prime
notizie sul lavoro di Ricci e in seguito su quello di
Riemann.
12
La geometria ellittica possiede un'interpretazione particolarmente importante nello
spazio fisico, fornendo il quadro matematico per la teoria della relatività generale.
Einstein nella sua teoria suppone che la curvatura dell'universo sia influenzata dalla
massa degli oggetti contenuti. Più un oggetto è denso, maggiore sarà la curvatura e
quindi in quel punto lo spazio sarà più "spigoloso". Nei pressi della Terra questo
fenomeno non è osservabile, ma già lo spazio nei pressi del Sole è sufficientemente
curvo da deviare leggermente i raggi delle stelle che lo attraversano. Il fenomeno
che si osserva è un apparente spostamento delle stelle dalla loro consueta
posizione.
I corpi celesti più interessanti in questo campo sono i Buchi Neri, la cui origine è data
da una stella massiccia che termina la sua vita in un corpo dalla densità e massa
altissime, tali da trattenere la luce che emette. La teoria di Einstein prevede che lo
spazio intorno ad un buco nero sia così deformato da provocare fenomeni molto
strani. Per esempio, un raggio di luce che passasse alla distanza di una volta e mezzo
il raggio dell'orizzonte degli eventi (limite oltre il quale nemmeno la luce può
sfuggire) si fermerebbe su un'orbita intorno all'oggetto, se passasse più vicino
formerebbe una curva molto stretta, simile ad una parabola, se passasse invece più
lontano formerebbe una curva un po’ più larga. Si può notare che, se i raggi di luce
rappresentano le rette, lo spazio intorno al buco nero è fortemente curvato, ed è
descrivibile solo con una geometria non euclidea.
Geometria iperbolica
Uno dei postulati logicamente equivalenti al V è quello di Playfair, quindi una buona
negazione del V può essere formulata come la negazione del postulato di Playfair.
Ovvero:
Esistono almeno un punto P ed una retta AB
tali
che:
I) P non è su AB né sul suo prolungamento
II) per P passano almeno 2 rette parallele ad
AB
Accettiamo la geometria neutrale e sostituiamo il V postulato con questo, saremo
allora
in
una
geometria
non
euclidea:
quella
iperbolica.
Come è possibile che vi siano due parallele alla stessa retta passanti per lo stesso
punto?
13
Siamo abituati a pensare che,
data AB ed il punto P, ci sia
solo la retta CD come parallela
alla prima.
fig.1
Ma proviamo a pensare che
ne esista una seconda:
pensiamo ad una retta
passante per P che non
coincida con CD.
fig.2
Diremmo che questa non possa essere parallela ad AB perché convinti che incontri
AB in un certo punto prima o poi. Ma proviamo a prescindere dall'apparenza del
disegno; possiamo dimostrare che il prolungamento di EF debba per forza
incontrare AB?
Teniamo presente che siamo in una geometria neutrale a cui abbiamo aggiunto la
negazione del postulato di Playfair, non abbiamo più il teorema 30 di Euclide che ci
dice che rette parallele ad una stessa retta sono parallele fra loro, quindi non deve
disturbarci il fatto che nel nostro caso EF e CD, entrambe parallele ad AB, si
incontrino in P.
Diremmo che questa non possa essere parallela ad AB perché convinti che incontri
AB in un certo punto prima o poi. Ma proviamo a prescindere dall'apparenza del
disegno; possiamo dimostrare che il prolungamento di EF debba per forza
incontrare AB?
Teniamo presente che siamo in una geometria neutrale a cui abbiamo aggiunto la
negazione del postulato di Playfair, non abbiamo più il teorema 30 di Euclide che ci
dice che rette parallele ad una stessa retta sono parallele fra loro, quindi non deve
disturbarci il fatto che nel nostro caso EF e CD, entrambe parallele ad AB, si
incontrino in P.
14
E ancora, non abbiamo più il
postulato di Euclide che ci
porterebbe a dire che,
poiché PQB+QPF<180°, le due
rette AB eEF si incontrano.
fig.3
E potremmo andare avanti ancora, scontrandoci con asserzioni logicamente
equivalenti al V postulato, e trovandoci a dover ogni volta ricordare che l'abbiamo
negato.
La verità è che nel disegno sembra talmente evidente che EF incontrerà AB che
crediamo di poterlo dimostrare, ma significherebbe dimostrare che AB è l'unica
parallela, ovvero dimostrare il postulato euclideo, problema che è stato spina nel
fianco dei matematici per 2000 anni.
Ai nostri occhi può sembrare che la negazione del postulato di Playfair sia
"incompatibile con la natura di una linea retta", per dirla alla Saccheri, ma dobbiamo
sforzarci di superare ed ingannare il consueto modo di pensare la geometria e non
spaventarci dal fatto che la geometria iperbolica sfugge da ogni tentativo di
rappresentazione intuitiva.
Proviamo a passare da un sistema assiomatico materiale, o teoria scientifica, a un
sistema assiomatico formale.
E convinciamoci che un sistema matematico (sistema assiomatico formale) è
sostanzialmente una pura struttura logica, alla quale si può annettere un significato
o meno. Forse in questo modo la geometria iperbolica ci disarmerà un po' meno.
Proviamo per un attimo a credere che le rette CD e EF siano entrambe parallele
ad AB senza pretendere che questo abbia il significato che siamo soliti attribuire alla
geometria che descrive il nostro mondo fisico.
15
Disegniamo
in
questo
modo
le
nostre rette:
fig.4
Il postulato iperbolico
Trattando la questione delle rette parallele abbiamo visto una negazione del
postulato di Playfair; da qui in poi svilupperemo la geometria iperbolica sulla base di
una versione più forte della negazione di tale postulato.
Postulato 1
Se P è un punto qualunque e AB una retta qualunque che non passa per P (nemmeno
se prolungata), allora vi sono due rette YPZ e WPX passanti per P tali che:
I) YPX non è un'unica retta,
II) YPZ e WPX sono entrambe parallele ad AB,
III) nessuna retta passante per P interna a ^YPX è parallela ad AB.
La condizione I afferma semplicemente che YPZ e WPX sono rette distinte.
Questo postulato comprende la negazione del postulato di Playfair vista in
precedenza, e in più due ulteriori affermazioni. Innanzitutto asserisce che l'esistenza
di parallele multiple è un fenomeno universale che si verifica per ogni punto P del
piano e per ogni retta AB non passante per esso. mentre il postulato di Playfair
garantiva che questo accadesse almeno una volta, per un punto ed una retta
particolari.
Inoltre le due parallele del postulato 1 sono le due parallele più basse, in ambo le
direzioni, passanti per P; la condizione III afferma infatti che una retta per P al di
sotto di una delle due non sarebbe parallela ad AB. Questa proprietà non era
16
specificata per le parallele del postulato di Playfair.
I termini primitivi della geometria iperbolica sono gli stessi che intervengono nella
geometria euclidea: punto, linea retta, superficie e superficie piana.
Anche gli altri termini vengono mantenuti, con l'aggiunta di nuovi che definiremo via
via.
Gli assiomi sono le nozioni comuni euclidee e tutti i postulati eccetto il V, che viene
sostituito dal POSTULATO 1. Questo fa sì che restino validi tutti i teoremi della
geometria neutrale, e cioè i teoremi che si possono dimostrare senza l'utilizzo del V
postulato.
Le parallele iperboliche
Teorema 1
Nella situazione descritta nel POSTULATO 1, ogni retta passante per P che
entra nell'angolo ^ZPX è parallela ad AB.
Le
rette
passanti
per
P
si
dividono
in
due
categorie:
una di cui fanno parte le infinite rette che entrano nell'angolo ^YPX, le quali, se
prolungate, intersecano AB o il suo prolungamento;
l'altra di cui fanno parte le rette YPZ e WPX e le infinite rette che entrano
nell'angolo ^ZPX, le quali, per quanto prolungate, non incontrano mai la
retta AB né il suo prolungamento. Queste ultime sono dunque parallele ad AB.
All'interno della seconda categoria YPZ e WPX occupano una posizione privilegiata,
segnano infatti il confine fra una categoria e l'altra.
Definizione 1
Nella situazione descritta dal POSTULATO 1, le rette YPZ e WPX si dicono
parallele asintotiche per P ad AB, e le rette passanti per P che entrano in ^ZPX
si dicono parallele divergenti per P ad AB.
17
Geometria dello spazio-tempo
Negli ultimi tre decenni la nostra concezione dello spazio e del tempo si è arricchita
notevolmente e ha conosciuto dei cambiamenti profondi grazie all’introduzione di
un insieme di nuove strutture matematiche non puntuali, non lineari e non
commutative, che formano quella che oggi viene chiamata geometria quantica.
Queste strutture sono il cuore delle teorie di Gauge non-abeliane e in grado di
unificare le particelle con i campi e la geometria dello spazio-tempo con la dinamica
dei fenomeni fisici tramite la descrizione e il modellamento delle interazioni
fondamentali. La costruzione allargata del modello standard della fisica, che ingloba
l’interazione elettrodebole (forza elettromagnetica più forza debole) e l’interazione
forte, è infatti interamente fondata sull’idea di gruppo di simmetria e di spazio con
connessione sul quale esso agisce. Se però, da un lato, un simile modello descrive
profondamente e in modo coerente le interazioni fisiche dovute alle tre forze
fondamentali esistenti in natura, dall’altro, esso è incapace di spiegare la forza di
gravitazione e, di conseguenza, di inglobare la relatività generale in un’immagine
unitaria del mondo fisico. I tentativi fatti negli ultimi anni per unificare le forze
elettrodebole e forte del modello standard nella teoria quantistica dei campi di
gauge con la forza gravitazionale della relatività generale hanno prodotto, dagli anni
Settanta in poi, una serie di sviluppi teorici fondamentali. La teoria delle supercorde
e la geometria non-commutativa appaiono tra i più significativi e profondi, sia sul
piano delle strutture matematiche che esse hanno contribuito a scoprire o a
18
chiarire, che su quello dei nuovi concetti filosofici introdotti.
L’idea filosofica di fondo sottostante a queste teorie, e in particolare alla teoria delle
supercorde, consiste nell’estendere l’idea dello spazio-tempo quadridimensionale
della relatività generale a dimensioni superiori, idea che fu proposta nella seconda
metà degli anni Venti del secolo scorso dal fisico Theodor Kaluza e dal matematico
Oscar Klein, ripresa e sviluppata in seguito, agli inizi degli anni Settanta, dalla teoria
della Supergravità. Nella teoria delle supercorde, si tratta in particolare di pensare i
nostri spazi a tre e quattro dimensioni come degli oggetti geometrici immersi in un
superspazio che comporta una o più dimensioni supplementari (per l’esattezza sei
dimensioni spaziali che si aggiungono alle tre dello spazio usuale e al tempo della
relatività). Queste dimensioni “nascoste” potrebbero avere un’influenza sulla gravità
a piccolissime distanze, e quindi aiutare a capire il comportamento di certi fenomeni
dovuto alla supposta natura quantistica della gravitazione alla scala della lunghezza
di Planck. Giova ricordare che all’origine dei tentativi di unificazione delle forze
attraverso la geometria cui si è appena accennato (che in realtà risalgono ai lavori di
Riemann e Clifford della seconda metà dell’Ottocento), c’era la necessità di spiegare
il conflitto tra la relatività generale di Einstein e la meccanica quantistica di Bohr e
Heisenberg. Due possibilità sono state considerate. La prima è stata l’elaborazione di
una teoria relativista consistente dei fenomeni quantistici, che ha cercato di
realizzare Einstein dagli anni Trenta del secolo scorso proponendo diverse
generalizzazioni della teoria del trasporto parallelo di Tullio Levi-Civita e dell’oggetto
geometrico di connessione di Elie Cartan, ma come si sa, tali tentativi non hanno
dato i risultati sperati. L’altra possibilità ha favorito l’elaborazione di un nuovo
quadro matematico capace di inglobare sia le forze quantistiche, che la gravitazione.
Si tratta dell’approccio sviluppato in particolare da Hermann Weyl (1929) e ripreso
da C. N. Yang e R. L. Mills (1954), che ha tentato fin dall’inizio di geometrizzare prima
la forza elettromagnetica, poi le forze deboli e forti nel contesto delle teorie di
Gauge abeliane e non-abeliane. Le teorie di Gauge hanno un profondo significato
geometrico, giacché si basano sui concetti fondamentali di spazio fibrato (o fibrato
principale) e di connessione con curvatura; questi concetti generalizzano la nozione
di spazio euclideo. Se M è una varietà differenziabile che rappresenta un modello di
spazio-tempo, e se in ciascun punto p di M si trova definito un sistema fisico con lo
spazio di stati interni j–1(p), allora una connessione sopra un oggetto geometrico
(uno spazio) è una regola o un processo che permette di trasportare il sistema lungo
le curve tracciate sulla varietà M. L’immagine geometrica che sta alla base della
teoria di Gauge rappresenta uno schema matematico tra i più profondi che si
19
conoscano in fisica, dal momento che permette la descrizione di un universo
idealizzato nel quale si considerano solo un piccolo numero di interazioni
fondamentali. Per esempio, un campo gravitazionale è una connessione che “vive”
nello spazio dei gradi interni di libertà di un giroscopio; la connessione permette di
seguire l’evoluzione del giroscopio nello spazio-tempo. Anche un campo
elettromagnetico è una connessione nello spazio dei gradi interni di libertà di un
elettrone quantico, e la connessione permette di seguire l’evoluzione dell’elettrone
nello spazio-tempo. Un campo di Yang-Mills è a sua volta una connessione nello
spazio dei gradi interni di libertà di un quark. L’idea essenziale è che lo stato interno
della materia, in ciascun punto e a ogni istante nello spazio-tempo, descrive una
connessione nel fibrato principale. La materia agisce sulla connessione imponendo
delle limitazioni alla sua curvatura (in altre parole, condizionando il tipo di
deformazioni che la curvatura conferisce allo spazio), e la connessione a sua volta
agisce sulla materia forzandola a propagarsi per trasporto parallelo lungo le “lineeuniverso” (le traiettorie del sistema fisico). Per questo, le celebri equazioni di
Einstein del 1915-16 che descrivono il campo gravitazionale, quelle di Dirac che
descrivono l’interazione tra il campo elettromagnetico e l’elettrone (una particella
dotata di spin), e infine quelle di Yang-Mills che descrivono le interazioni dovute a
tutte le forze fondamentali della natura tranne la gravità, sono esattamente
l’espressione
e
la
realizzazione
di
questa
idea.
I concetti di fibrato principale e di connessione sono così diventati tra i costituenti
più importanti della fisica. Le teorie quantistiche di gauge (o teorie di Yang-Mills)
sono infatti costruite a partire dall’idea che a ogni entità fondamentale della teoria
fisica corrisponde un concetto della geometria e topologia differenziali; questi
concetti possono essere di natura locale, come la curvatura, o globale, come il
fibrato principale. Così, ad esempio, l’intensità del campo elettromagnetico
s’identifica con la curvatura della connessione; l’integrale d’azione corrisponde
essenzialmente alla misura globale della curvatura; certi invarianti topologici e
algebrici appartenenti alla teoria delle classi caratteristiche possono essere associati
alla descrizione della carica della particella nel senso di Yang-Mills. Più
generalmente, esiste una corrispondenza diretta tra i concetti della teoria dei campi
quantistici di gauge e quelli della teoria geometrica e topologica dei fibrati.
È il caso di sottolineare che la relatività generale è stata la prima realizzazione
importante di questo programma di geometrizzazione della fisica. Una delle sue
caratteristiche fondamentali è di ammettere, per i fenomeni a scala macroscopica
(cioè dell’intero universo) che essa spiega con grande precisione, l’esistenza di un
20
gruppo matematico di simmetrie che lasciano localmente invarianti le leggi di quegli
stessi fenomeni. In altre parole, si può effettuare qualsiasi trasformazione del
sistema di coordinate curvilinee nell’intorno di un punto dato in questo stesso
spazio-tempo, e definito mediante una metrica pseudo-riemanniana di tipo
iperbolico, senza che le leggi fisiche dei fenomeni ne risultino alterate. Il che significa
che le simmetrie della relatività generale non hanno un significato globale. Per
simmetria globale si intende una simmetria per via della quale una trasformazione
può essere eseguita uniformemente su tutti i punti dello spazio, mentre nel caso di
una simmetria locale, ciascun punto è trasformato indipendentemente l’uno
dall’altro. La teoria della relatività generale, cosi come la teoria elettromagnetica di
Maxwell, è dunque una teoria di gauge locale. In effetti, il fatto che intervengano dei
campi materiali indica chiaramente che la geometria dello spazio-tempo,
caratteristica dei fenomeni a larga scala studiati dalla relatività generale, si trova a
essere condizionata dalla più o meno grande densità di materia presente nel campo.
La simmetria sulla quale si fonda la relatività generale non riguarda tanto un campo
fisico che si propaga attraverso lo spazio e il tempo, quanto la stessa struttura
geometrica dello spazio-tempo. Detto diversamente, la relatività generale non
considera le cosiddette simmetrie interne, che concernono le proprietà dei campi
quantistici come la fase, la carica, ecc., né considera le interazioni tra le particelle e
gli altri campi quantistici della materia alla scala subatomica. Il punto importante è
che l’insieme dello spazio-tempo della relatività ristretta e dello spazio interno della
meccanica quantistica presenta una struttura matematica molto più ricca di quella
rispettiva di ogni singola teoria: si tratta, più precisamente, di una struttura di spazio
fibrato nel quale le trasformazioni del gruppo di simmetrie interne – un gruppo di
Lie non-abeliano – generano degli spostamenti lungo le fibre, e i campi di gauge
corrispondono alle connessioni di Cartan.
I Quadrivettori
Nella Fisica Classica di Newton-Galileo, il tempo t è lo stesso per ogni osservatore e,
quindi, per descrivere il moto di un corpo ( punto materiale) in diversi sistemi
inerziali è sufficiente trovare come cambiano le coordinate spaziali x, y e z che
individuano la posizione del corpo ad un generico istante t. Il problema è, quindi,
intrinsecamente tri-dimensionale e completamente descritto dal vettore tridimensionale r (t ) = (x(t ), y(t ), z(t )). Nel caso della Fisica Relativistica, invece, anche
il tempo dipende dalla posizione in cui esso viene misurato e, quindi, per poter
descrivere interamente il moto di un corpo non basta conoscere le sue coordinate
21
spaziali x, y, z in un dato Riferimento inerziale ma si deve anche conoscere il tempo
misurato da un orologio che si trovi nel punto di coordinate x,y, z nello stesso
Riferimento. Se cambiamo riferimento, non solo cambieranno le coordinate spaziali
ma anche quella temporale. Quindi, mentre la Fisica Classica è intrinsicamente tridimensionale, la Fisica Relativistica è quadri-dimensionale. In particolare, per
individuare completamente la posizione di un corpo nello spazio-tempo relativistico
rispetto ad una certa origine si dovranno dare 4 coordinate: tre coordinate spaziali
x,y, z e una temporale t. Possiamo, perciò, introdurre un oggetto rappresentato da
quattro coordinate
R = (x,y,z,t ) (1)
che viene detto quadrivettore nello spazio-tempo [ come (x,y,z) rappresentava un
vettore nello spazio]. Ora, come abbiamo già osservato, le dimensioni delle
coordinate spaziali ( metri) sono diverse da quelle delle coordinate temporali
(secondi). La differenza ha un'origine storica dovuta al fatto che, prima della Fisica
Relativistica, il tempo e lo spazio apparivano entità completamente differenti e,
quindi, era apparso naturale definirli utilizzando unità di misura diverse. Adesso,
invece, abbiamo trovato che, nel passaggio da un riferimento inerziale ad un altro, le
coordinate spaziali e temporali si vengono a mescolare le une nelle altre attraverso
le Trasformazioni di Lorenz in modo assai simile a quanto avviene per le coordinate
spaziali x,y,z in una rotazione. Dunque, in Relatività, risulta più naturale usare per le
coordinate spaziali e temporali le stesse unità. In effetti, con questa scelta, le
trasformazioni di Lorentz per la variabile spaziale x e per quella temporale risultano
totalmente simmetriche. Ad esempio, possiamo usare come unità di tempo il metroluce che corrisponde al tempo impiegato dalla luce nel vuoto per percorrere un
metro. In alternativa, potremmo anche continuare a definire il secondo come unità
di tempo e utilizzare come unità di lunghezza il secondo luce definito come lo spazio
percorso dalla luce in un secondo ( circa 300.000 km). Qui decidiamo di misurare il
tempo in metri-luce. Se il tempo espresso in secondi è t, il corrispondente tempo
espresso
in
metri
(
metri-luce)
è
t = ct, (2) dove c » 300.000 Km/s.
Con questo nuovo tempo, espresso in metri, la velocità v = Dx/Dt di un corpo risulta
un numero puro adimensionale poichè Dx e Dt hanno le stesse dimensioni.
22
In particolare, v = Dx/Dt = Dx/(cDt )=V/c dove V indica la velocità del corpo nelle
unità standard ( m/s). Dunque, la velocità di un corpo nelle nuove unità di misura
viene a coincidere con il parametro relativistico b definito in precedenza. In
particolare, nelle nuove unità la velocità della luce è pari a c/c = 1. Se utilizziamo
queste nuove unità di misura, quando diremo che un corpo viaggia con velocità v =
0.1, significherà che esso viaggia con una velocità pari a 0.1 volte quella della luce,
cioè
circa
30.000km/s.
Per ottenere la forma delle equazioni di Lorentz con il tempo misurato in metri-luce,
basterà, perciò, sostituire in esse al posto di t il nuovo tempo t ( t = ct ) , e al posto di
c il valore c =1 ricordandosi che, ora, la velocità v rappresenta il parametro
adimensionale b =V/c. Per ritornare alle relazioni scritte nelle solite unità, basterà
sostituire al posto di t il valore ct e al posto di v il valore V/c. Riassumendo, nelle
nuove unità valgono le uguaglianze:
c = 1 , b = v , g = 1 / ( 1- v2)
La distribuzione delle masse-energia determina una distorsione dello spazio-tempo;
un corpo libero di muoversi, anche la luce, si muoverà allora sempre lungo le
geodetiche dello spazio-tempo, che però adesso possono non coincidere più (in
presenza di masse o concentrazioni di energia) con delle rette come nella geometria
euclidea (vedere anche geometrie non euclidee), ma sono generalmente delle
curve.
Lo spazio-tempo di Minkowski allora non potrà più essere descritto, come nella
relatività speciale, dalla geometria euclidea (seppure a 4 dimensioni) e in esso non
potremo più considerare sistemi di riferimento cartesiani ortogonali, ma sistemi di
riferimento curvilinei, detti gaussiani.
Sappiamo tuttavia, in base al principio di equivalenza, che si possono sempre
eliminare localmente gli effetti del campo gravitazionale scegliendo un sistema di
riferimento in caduta libera. Ciò corrisponde a considerare localmente un sistema di
riferimento cartesiano, poiché la coincidenza con le coordinate curvilinee del
sistema di riferimento, in piccole regioni dello spazio-tempo, diviene abbastanza
buona.
23
Un concetto necessario per descrivere lo spazio-tempo deformato è comunque
quello di curvatura dello spazio (nella quarta dimensione ct). Per illustrare il
concetto il più semplicemente possibile ci si può aiutare con qualche esempio tratto
dalla geometria in tre dimensioni.
Si immagini allora lo spazio-tempo a 4 dimensioni (3 spaziali ed una temporale)
ridotto a due sole dimensioni spaziali ed ad una temporale. Si può pensare allo
spazio (a 3 dimensioni) come se fosse la superficie (a 2 dimensioni) di un telo
elastico nella terza dimensione che rappresenterebbe il tempo.
NCLUSIONE
CONSIDERAZIONI
Il quinto postulato di Euclide costituisce un bivio:
• Accettandolo si ha la geometria euclidea
• Negandolo si ottengono le altre geometrie
Non c’è una geometria migliore o “più vera” delle altre
Nel suo trattato La Scienza e l’Ipotesi lo stesso Poincaré esprime questo concetto:
Se la geometria fosse una scienza sperimentale non sarebbe una scienza esatta e
andrebbe soggetta ad una continua revisione.
Che si deve quindi pensare della questione circa la verità della geometria?
Essa non ha alcun senso. Sarebbe come domandare se il sistema metrico sia vero e
false le antiche misure; se siano vere le coordinate cartesiane e false quelle polari.
vera” de
e alternative è migliore o “più
Una geometria non può essere più vera di un’altra; essa può essere soltanto più
comoda.ell
24