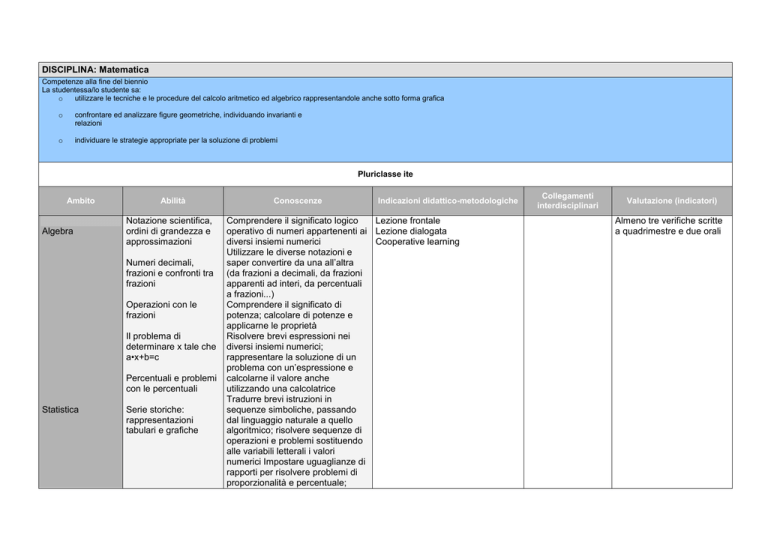
DISCIPLINA: Matematica
Competenze alla fine del biennio
La studentessa/lo studente sa:
o
utilizzare le tecniche e le procedure del calcolo aritmetico ed algebrico rappresentandole anche sotto forma grafica
o
confrontare ed analizzare figure geometriche, individuando invarianti e
relazioni
o
individuare le strategie appropriate per la soluzione di problemi
Pluriclasse ite
Ambito
Algebra
Abilità
Notazione scientifica,
ordini di grandezza e
approssimazioni
Numeri decimali,
frazioni e confronti tra
frazioni
Operazioni con le
frazioni
Il problema di
determinare x tale che
a•x+b=c
Percentuali e problemi
con le percentuali
Statistica
Serie storiche:
rappresentazioni
tabulari e grafiche
Conoscenze
Indicazioni didattico-metodologiche
Comprendere il significato logico
Lezione frontale
operativo di numeri appartenenti ai Lezione dialogata
diversi insiemi numerici
Cooperative learning
Utilizzare le diverse notazioni e
saper convertire da una all’altra
(da frazioni a decimali, da frazioni
apparenti ad interi, da percentuali
a frazioni...)
Comprendere il significato di
potenza; calcolare di potenze e
applicarne le proprietà
Risolvere brevi espressioni nei
diversi insiemi numerici;
rappresentare la soluzione di un
problema con un’espressione e
calcolarne il valore anche
utilizzando una calcolatrice
Tradurre brevi istruzioni in
sequenze simboliche, passando
dal linguaggio naturale a quello
algoritmico; risolvere sequenze di
operazioni e problemi sostituendo
alle variabili letterali i valori
numerici Impostare uguaglianze di
rapporti per risolvere problemi di
proporzionalità e percentuale;
Collegamenti
interdisciplinari
Valutazione (indicatori)
Almeno tre verifiche scritte
a quadrimestre e due orali
Geometri analitica
risolvere semplici problemi diretti e
inversi
Risolvere equazioni e disequazioni
di primo e secondo grado e
verificare la correttezza dei
procedimenti utilizzati Risolvere
sistemi di equazioni e disequazioni
Le funzioni lineari:
di primo e secondo grado e
tabelle, grafici e
verificarne la correttezza dei
formule
risultati Applicare il concetto di
vettore a semplici situazioni
Le funzioni lineari:
problematiche, eventualmente
pendenza ed intercetta anche di fisica
Geometria
Zero di una funzione
Riconoscere i principali enti, figure
lineare – Equazioni
e luoghi geometrici e descriverli
lineari in un’incognita
con linguaggio naturale
Costruire figure anche utilizzando
Problemi sulle funzioni programmi di geometria dinamica
lineari
Individuare le proprietà essenziali
delle figure e riconoscerle in
Segno e confronto di
situazioni concrete Applicare le
funzioni lineari
principali formule relative alla retta
e alle figure geometriche sul piano
Le funzioni lineari:
cartesiano
disequazioni e sistemi Comprendere i principali passaggi
di equazioni lineari
logici di una dimostrazione
Risolvere triangoli in casi semplici,
anche della fisica
Dall’aritmetica
Relazioni e funzioni
all’algebra
Leggere e interpretare tabelle e
grafici in termini di corrispondenze
Addizioni e
fra elementi di due insiemi
moltiplicazioni di
Rappresentare sul piano
polinomi: espressioni
cartesiano il grafico di una
polinomiali
funzione
Rappresentare graficamente
Prodotti notevoli
equazioni di primo e secondo
grado; comprendere il concetto di
L’algebra come
equazione e quello di funzione
strumento di pensiero Elaborare e gestire semplici calcoli
Introduzione al
concetto di funzione:
macchine input-output,
tabelle, grafici e
formule
Algebra
La divisione tra
polinomi e il teorema
del resto
attraverso un foglio elettronico
Elaborare e gestire un foglio
elettronico per rappresentare in
forma grafica i risultati dei calcoli
eseguiti
Dati e previsioni
Raccogliere, organizzare e
rappresentare un insieme di dati
Rappresentare classi di dati
mediante istogrammi e diagrammi
a torta
Calcolare i valori medi e alcune
misure di variabilità di una
distribuzione
Calcolare la probabilità di eventi
elementari












