28/05/2012
Statistica parametrica
e non parametrica
Per un campione univariato
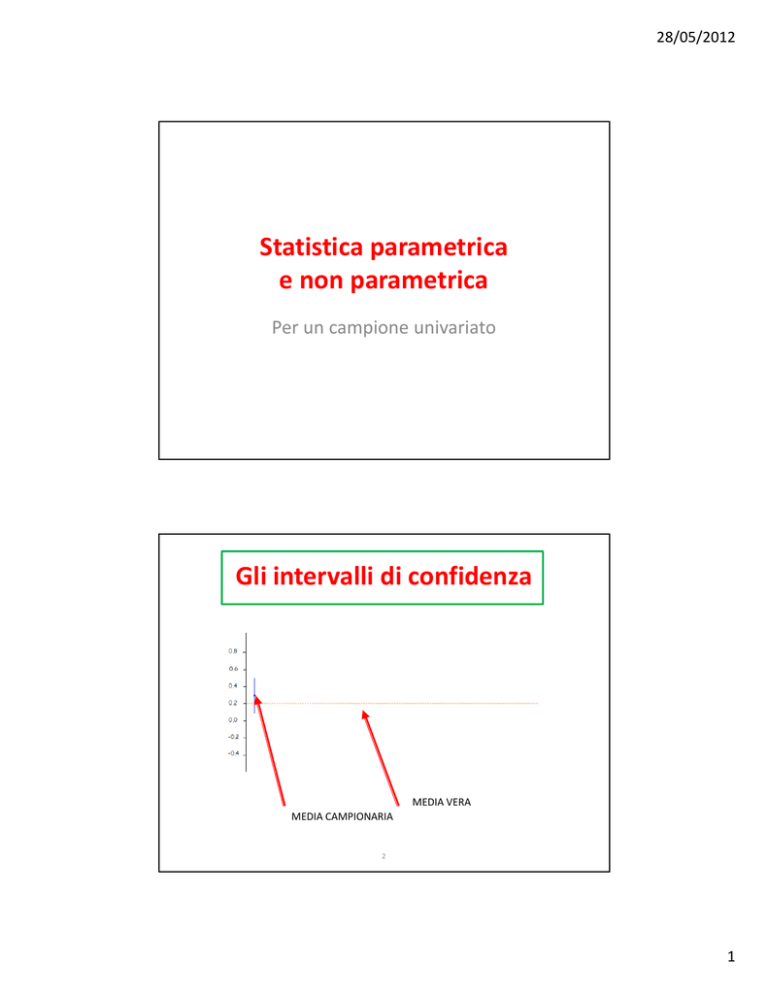
Gli intervalli di confidenza
MEDIA VERA
MEDIA CAMPIONARIA
2
1
28/05/2012
Gli intervalli di confidenza
3
Gli intervalli di confidenza
4
Una introduzione alla
Biostatistica
2
28/05/2012
Gli intervalli di confidenza
Nel 95% dei casi, l’intervallo di confidenza conterrà la media della
popolazione.
Come si calcolano gli estremi?
Uno studio di avvocati
ha 5 associati.
All’incontro settimanale che svolgono,
ciascuno riporta il
numero di ore di lavoro
fatturato. Nell’ultima
settimana si è avuto:
ESEMPIO
Partner
Hours
Dunn
22
Hardy
26
Kiers
30
Malory
26
Tillman
22
Se 2 associati vengono
selezionati a caso, quanti
possibili campioni si
possono ottenere?
3
28/05/2012
10 differenti campioni
Partners
1,2
1,3
1,4
1,5
2,3
2,4
2,5
3,4
3,5
4,5
Totale
48
52
48
44
56
52
48
56
52
48
Media
24
26
24
22
28
26
24
28
26
24
E’ possibile definire una variabile aleatoria media campionaria, a
partire dal campione casuale.
La distribuzione di probabilità di questa variabile “media campionaria”
risulta essere:
Media
campionaria
Frequenza
Frequenza
relative = prob
22
1
1/10
24
4
4/10
26
3
3/10
28
2
2/10
Media delle medie campionarie
µX =
22(1) + 24(4) + 26(3) + 28(2)
= 25.2
10
4
28/05/2012
Partner
Hours
Dunn
22
Hardy
26
Kiers
30
Malory
26
Tillman
22
La media della popolazione
risulta essere:
Quindi la media
della media
campionaria è
proprio uguale alla
media della
popolazione.
Media della popolazione
µ=
22 + 26 + 30 + 26 + 22
= 25.2
5
Questo risultato
empirico può essere
mostrato per via
teorica
Effettuiamo il calcolo della varianza della media campionaria
s X2 =
Media
campionaria
Frequenza
Frequenza
relative = prob
22
1
1/10
24
4
4/10
26
3
3/10
28
2
2/10
1
1
1
1
2
2
2
2
( 22 − 25.2 ) + ( 24 − 25.2 ) × 4 + ( 26 − 25.2 ) × 3 + ( 28 − 25.2 ) × 2 = 3.36
10
10
10
10
5
28/05/2012
Mentre per la varianza della popolazione, si ha
Partner
Hours
Dunn
22
Hardy
26
Kiers
30
Malory
26
Tillman
22
s X2 =
Anche questo risultato si
può mostrare per via
teorica…
2
2
1
2
2
2
( 22 − 25.2 ) + ( 26 − 25.2 ) + ( 30 − 25.2 ) = 6.08
5
5
5
2
X
Osserviamo che risulta s =
σ2
n
, con n=2
La deviazione standard della media campionaria prende il nome di
errore standard o precisione
Abbiamo visto che E[ X ] = µ e Var[ X ] =
σ2
n
Se la popolazione da cui proviene il campione casuale ha legge
σ2
gaussiana ⇒ X ≈ N µ ,
n
Se la popolazione da cui proviene il campione casuale non ha legge
σ2
gaussiana ⇒ X ≈ N µ , per n>30
n
6
28/05/2012
GLI INTERVALLI DI CONFIDENZA
X⇒
X −µ
⇒ Z ≈ N ( 0,1) ⇒
σ/ n
P ( − zα / 2 ≤ Z ≤ zα /2 ) = 1 − α
X −µ
P − zα /2 ≤
≤ zα /2 = 1 − α
σ/ n
σ
σ
≤ µ ≤ X + zα /2
P X − zα /2
= 1−α
n
n
ESERCIZIO: I dati seguenti rappresentano le misure del
diametro di 40 specie di ammoniti (file esempio4.txt).
1) Generare un rapporto di statistica descrittiva e
commentarlo.
2) Formulare una ipotesi sulla distribuzione della
popolazione.
3) Costruire un intervallo di confidenza per la media
della popolazione.
7
28/05/2012
Per α = 0.05 ⇒ P(3.34 < µ < 3.53) = 0.95
media
3,44
media
3,44
st.dev.
0,308
st.dev.
0,308
quantile 1,959964
quantile
1,644854
inf
3,344552
inf
3,359897
sup
3,535448
sup
3,520197
taglia
40
taglia
40
Quali conclusioni si traggono?
Per α = 0.10 ⇒ P(3.35 < µ < 3.52) = 0.90
Nell’esempio precedente abbiamo usato la varianza
campionaria!! E’ legittimo?
NO
Per usare l’informazione che la media campionaria ha legge
gaussiana, c’è bisogno di conoscere la varianza della popolazione
Quando non si ha a disposizione questa informazione, e si
usa la varianza campionaria, la distribuzione di probabilità
della media campionaria non è più gaussiana.
VARIABILE ALEATORIA T-STUDENT
8
28/05/2012
X −µ
⇒ N (0,1)
σ/ n
X −µ
⇒ Tn −1
S/ n
E [ X ] = 0 se n>1, altrimenti è indefinita
NB: fondamentale è l’ipotesi che la popolazione sia gaussiana.
Al crescere di n converge
a una gaussiana standard.
E [ X ] = 0 se n>1, altrimenti è indefinita
Var[ X ] =
n
se n>2 (altrimenti indefinita)
n−2
9
28/05/2012
INTERVALLI DI CONFIDENZA
PER LA MEDIA,
VARIANZA INCOGNITA
−tα / 2, n −1 tα / 2, n −1
ESERCIZIO: Nell’esempio precedente calcolare l’intervallo
di confidenza per la media con
la varianza incognita.
S
S
≤ µ ≤ X + tα / 2, n −1
P X − tα / 2, n −1
=1−α
n
n
In Statview c’è una procedura per il calcolo dell’IC
quando la varianza è incognita
10
28/05/2012
Un caso a parte…
Popolazione di Bernoulli X 1 , X 2 ,…, X n
X 1 , X 2 ,…, X n i.i.d. ⇒ X 1 + X 2 + ⋯ + X n ∼ N ( µ ,σ 2 )
σ
σ
P X − zα /2
≤ µ ≤ X + zα /2
= 1−α
n
n
%successi
p(1 − p )
INTERPRETAZIONE
11
28/05/2012
ESEMPIO:
Su 1000 rocce esaminate, 480 hanno tracce di un certo materiale.
Determinare l’intervallo di confidenza per la percentuale di rocce
che contengono quel materiale.
p
0,48
quan.inf. 1,959964
quan.sup. -1,95996
semi
0,015799
(0.465,0.495)
50% non è incluso!
INTERVALLO DI CONFIDENZA PER LA VARIANZA
Serve per verificare se la varianza di una certa popolazione ha un
valore prestabilito.
PDF distribuzione chi-quadrato
0.5
df=2
df=4
df=8
df=16
0.45
0.4
PUNTO DI PARTENZA
0.35
0.3
(n − 1) S 2
0.25
0.2
σ
0.15
2
≈ χ n2−1
0.1
0.05
0
0
1
2
3
4
5
6
7
8
9
10
DISTRIBUZIONE CHI-QUADRATO
12
28/05/2012
E[ X ] = df , Var[ X ] = 2 × df
n
Teor : Se { X i }i =1 sono variabili aleatorie gaussiane i.i.d., allora
W=X 12 + X 22 + ⋯ + X n2 è una variabile aleatoria chi-quadrato con
n gradi di libertà
(n − 1) S
σ2
2
=
n
1
σ
2
n
X −X) ≈∑
2 ∑( i
i =1
(X
i =1
i
−X)
2
σ2
La definizione dei quantili è più articolata, essendo la distribuzione asimmetrica
2
1− α / 2
χ
χα2 / 2
P ( χ12−α / 2 < χ 2 < χα2 / 2 ) = 1 − α
13
28/05/2012
P ( χ12−α / 2 < χ 2 < χα2 / 2 ) = 1 − α
2
S2
2
P χ1−α / 2 < (n − 1) 2 < χα / 2 = 1 − α
σ
χ12−α / 2
1
χα2 / 2
P
< 2<
=1−α
2
2
σ
(n − 1) S
( n − 1) S
(n − 1) S 2
(n − 1) S 2
2
P
<σ <
=1−α
2
2
χ
χ
α /2
1−α / 2
ESERCIZIO: Nell’esempio precedente calcolare l’intervallo
di confidenza per la varianza.
14
28/05/2012
Proviamo ad usare Excel.
var
df
quantile
quantile
inf
sup
0,095
39
23,65432
58,12006
0,063747
0,156631
TEST DI IPOTESI
Supponiamo di voler verificare che un assegnato campione casuale
ha media 50.
Supponiamo che calcolata la media campionaria, questa risulti essere 50.7.
In base a questa affermazione possiamo affermare che “la media della
popolazione è 50”?
?
?
REGIONE
CRITICA
REGIONE DI
ACCETTAZIONE
REGIONE
CRITICA
15
28/05/2012
X
REGIONE
CRITICA
REGIONE DI
ACCETTAZIONE
Qual
è la
scelta
più
naturale
per gli
estremi
della
regione
di
accettazione?
REGIONE
CRITICA
Si rigetta l’ipotesi nulla se …
x
16
28/05/2012
Non si rigetta l’ipotesi nulla se …
x
µ0 = 50
σ
σ
≤ X ≤ µ0 + zα / 2
P µ0 − zα / 2
=1−α
n
n
17
28/05/2012
Nel formulare un test di ipotesi
H 0 : µ = µ0
H1 : µ ≠ µ 0
IPOTESI NULLA
IPOTESI ALTERNATIVA
TAVOLA DEGLI ERRORI
H 0 vera
H 0 falsa
si rigetta H 0
errore I tipo
decisione corretta
non si rigetta H 0
decisione corretta
errore II tipo
Errore
di I tipo?
µ0
σ
σ
P µ0 − zα / 2
≤ X ≤ µ0 + zα / 2
=1−α
n
n
18
28/05/2012
Errore
di II tipo?
Supponiamo che
l’ipotesi alternativa
sia che la media è
pari a 51.
Per calcolare la probabilità di commettere l’errore di II tipo,
c’è bisogno di conoscere l’ipotesi alternativa…
Si fissa allora la probabilità di commettere l’errore di I tipo e si
determina la regione di accettazione.
ESEMPIO: Dieci campioni di roccia sono stati analizzati per il contenuto
in materia organica.
(a) Determinare l’intervallo di confidenza al 95% .
(b) Effettuare un test per verificare se è ragionevole ipotizzare un contenuto medio della roccia pari al 18.0%.
19
28/05/2012
1) Effettuare un norm-plot per supporre che la popolazione sia ragionevolmente gaussiana.
dati
2
1,5
1
0,5
0
dati
0
5
10
15
20
25
30
35
-0,5
-1
-1,5
-2
2) Non essendo nota la varianza, l’intervallo di confidenza va calcolato
usando la variabile aleatoria T-student. Usiamo la function di Statview.
6.53
6.53
P 20.5 − 2.2621 ×
≤ µ ≤ 20.5 + 2.2621 ×
= 0.95
10
10
3) Per il test
6.53
6.53
P 20.5 − 2.2621×
≤ µ ≤ 20.5 + 2.2621×
= 0.95
10
10
18
X
18
20
28/05/2012
H 0 : µ = 18
H1 : µ ≠ 18
REGIONE DI ACCETTAZIONE
18 − tα / 2, n −1
H 0 non si rigetta
S
n
,18 + tα / 2, n −1
SI
S
n
x ∈?
H 0 si rigetta NO
LEGAME TRA INTERVALLO DI CONFIDENZA E REGIONE DI
ACCETTAZIONE
REGIONE DI ACCETTAZIONE
18 − tα / 2, n −1
S
S
,18 + tα / 2, n −1
n
n
x ∈?
INTERVALLO DI CONFIDENZA
µ ∈?
X − tα / 2, n −1
S
S
, X + tα / 2, n −1
n
n
21
28/05/2012
REGIONE DI ACCETTAZIONE=(13.32, 22.67)
H 0 non si rigetta
20.5 ∈
Per leggere l’esito del test con STATVIEW, è necessario introdurre il
concetto di p-value.
E ' l'area a destra
del valore della
statistica x
Se p > 0.025
⇒ H 0 non si rigetta
Se p < 0.025
⇒ H 0 si rigetta
Il p-value è l’area
a destra della statistica
test
x
22
28/05/2012
x − 18
S/ n
Essendo p > 0.025
⇒ H 0 non si rigetta
DECISIONE DEBOLE: non siamo in grado di valutare la probabilità di commettere l’errore di II tipo.
DECISIONE FORTE: quando si rigetta l’ipotesi nulla, sappiamo
di commettere un errore di I tipo con probabilità 5%.
Si può calcolare l’errore di II tipo, al variare dell’ipotesi alternativa.
P ( X ∈ Regione di accettazione )
23
28/05/2012
Si definisce CURVA POTENZA associata al test, il complementare ad
uno della probabilità di commettere un errore di II tipo = probabilità
di rigettare l’ipotesi nulla quando è falsa.
Power curve
1.005
1
0.995
0.99
0.985
0.98
0.975
0.97
14
15
16
17
18
19
20
21
22
TEST DI IPOTESI SULLA VARIANZA
Serve per verificare se la varianza di una certa popolazione ha un
valore prestabilito.
H0 : σ = σ 0
H1 : σ ≠ σ 0
PDF distribuzione chi-quadrato
0.5
df=2
df=4
df=8
df=16
0.45
0.4
0.35
Statistica Test
0.3
0.25
(n − 1) S 2
0.2
0.15
σ
0.1
0.05
0
0
1
2
3
4
5
6
7
8
9
2
≈ χ n2−1
10
DISTRIBUZIONE CHI-QUADRATO
24
28/05/2012
Attenzione : il valore della statistica test è molto alto! Bisogna scegliere opportunamente
l’ipotesi alternativa
IPOTESI nulla
36
IPOTESI NULLA
40
IPOTESI nulla
46
TEST PER LA BONTA’ DI ADATTAMENTO
Empirical CDF
1
Il seguente grafico
riporta la funzione di
ripartizione empirica
del campione
AMMONITI
e la funzione di ripartizione
teorica di una popolazione
gaussiana con media, la
media campionaria e con
varianza, la varianza
campionaria.
0.9
0.8
0.7
F(x)
0.6
0.5
0.4
0.3
0.2
0.1
0
2.8
3
3.2
3.4
3.6
3.8
4
4.2
x
Possiamo ritenere le due curve sufficientemente “vicine”,
in modo da ritenere valido il modello stocastico gaussiano
per la popolazione da cui il campione casuale è estratto?
25
28/05/2012
TEST DI KOLMOGOROV-SMIRNOV
STATISTICA TEST ⇒ D = max F ( xi ) − Fˆ ( xi )
i
Per l’esecuzione del test in EXCEL è necessario effettuare i seguenti passi:
a) Ordinare i dati in ordine crescente
b) Costruire la funzione di ripartizione empirica
26
28/05/2012
c) Costruire la funzione di ripartizione teorica
d) Calcolare la differenza in valore assoluto tra le due funzioni:
e) Calcolare il massimo della differenza in valore assoluto tra le due funzioni:
27
28/05/2012
f) Confrontare il valore così ottenuto con il quantile
della variabile aleatoria D.
dα ,n
associato alla distribuzione
Le tavole dei quantili sono disponibili all’indirizzo
http://www.unibas.it/utenti/dinardo/tavola.html
f) Come si legge la tavola: sulla riga corrispondente alla taglia n=40, si sceglie il valore di
riferimento nella colonna relativa a 1 - α
….
Quindi possiamo
ritenere valido
il modello stocastico gaussiano
per la popolazione da cui il campione casuale è
estratto…
da confrontare 0,072005
28
28/05/2012
STATISTICA NON PARAMETRICA
IN STATVIEW
• Nel caso di campioni appartenenti a distribuzioni non normali è possibile applicare una serie di test equivalenti a quelli descritti nel capitolo precedente, detti test non parametrici.
• I test non parametrici non hanno la stessa efficacia dei test
parametrici.
• Quando applicati a campioni gaussiani, risultano più potenti.
• L’ampiezza del campione casuale può essere anche molto
piccola.
• Particolarmente utili nel caso i dati del campione siano sot-
to forma di ranghi (=posto che il dato occupa nel campione
casuale ordinato).
29
28/05/2012
TEST SUI SEGNI tra i tests non parametrici più diffusi
H 0 : M = M 0
H1 : M ≠ M 0
E’ un test effettuato sulla mediana della popolazione anzicché sulla
media (che è un Indice di posizione meno robusto).
IDEA:
50%
50%
x(1) , x(2) ,…, x( M ) ,…, x( n )
Se indichiamo con
R = num. dati del campione casuale ≤ M 0
R ∼ B(n,0.5)
p=1/2
0.12
Num. di dati che cadono
a sinistra di M 0 deve essere all’incirca la metà
della taglia del campione.
0.1
0.08
0.06
0.04
Se il numero di dati che
cadono a sinistra di M 0 è
troppo elevato (o troppo
basso) , la pdf corrispondenSe questi valori sono troppo bassi…. te assumerà valori bassi.
0.02
0
0
5
10
15
20
25
30
35
40
45
50
si rigetta l’ipotesi nulla
30
28/05/2012
ESEMPIO:
IL PRIMO RISULTATO E’:
correzione
IL CAMPIONE CASUALE HA
MEDIANA PARI A 10.
31
28/05/2012
ESERCIZIO: I seguenti dati si riferiscono ad intensita’ di terremoti registrati in un dato sito.
Effettuare una anlisi dei dati completa (terremotI)
32












