alma mater studiorum università di bologna

ALMA MATER STUDIORUM
UNIVERSITÀ DI BOLOGNA
Scuola di Fisica
Corso di Laurea Triennale in Astronomia
Il metodo WKB e sue applicazioni in
fisica nucleare
Relatore:
Chia.mo Prof. Francesco Ravanini
Candidato:
Claudio Di Gregorio
II Sessione
Anno Accademico 2011-12
Indice
1 Introduzione
1
1.1
Cenni preliminari . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.2
Buca rettangolare simmetrica . . . . . . . . . . . . . . . . . . . . . .
3
1.2.1
Stati legati
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.2.2
Stati del continuo . . . . . . . . . . . . . . . . . . . . . . . . .
7
Barriera di potenziale ed effetto tunnel . . . . . . . . . . . . . . . . .
9
1.3
2 L’approssimazione WKB
2.1
13
Il caso “classico” . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.1.1
Buca di potenziale con fondo irregolare . . . . . . . . . . . . . 17
2.2
Barriera di potenziale ed effetto tunnel . . . . . . . . . . . . . . . . . 18
2.3
Le formule di connessione . . . . . . . . . . . . . . . . . . . . . . . . 20
2.3.1
Buca di potenziale con pareti curve . . . . . . . . . . . . . . . 24
3 L’approssimazione WKB in un campo a simmetria centrale
3.1
27
L’urto deutone-nucleo pesante . . . . . . . . . . . . . . . . . . . . . . 30
A Probabilità di transizione in regime di semi-classicità
35
A.1 Riflessione al di sopra di una barriera di
potenziale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Bibliografia
37
INDICE
Capitolo 1
Introduzione
Da sempre lo scopo ultimo della fisica è quello di risolvere, mediante formule teoriche, problemi pratici spesso legati alla vita di tutti i giorni. Non di rado però anche
l’utilizzo delle teorie più complesse non è sufficiente alla soluzione esatta di tali problemi; si ricorre perciò a delle approssimazioni, dei metodi di calcolo che pur non
fornendo il risultato esatto, giungono ad una soluzione ragionevolmente accettabile.
A questa si giungerà prima individuando un problema “ridotto” che si possa risolvere
esattamente, quindi aggiungendo a tale sistema “imperturbato” delle perturbazioni,
che supporremo essere governate da un parametro piccolo rispetto alle altre grandezze fisiche presenti, così da modificare i valori delle quantità fisiche del problema.
Da questo punto di vista la meccanica quantistica non fa eccezione, facendo uso
delle approssimazioni in gran parte degli argomenti che tratta. Basti pensare al
metodo di approssimazione di Born-Oppenheimer e all’approssimazione orbitalica
per la chimica quantistica, al metodo variazionale di Rayleigh-Ritz per il calcolo
approssimato degli stati fondamentali e a molti altri metodi di approssimazione che
hanno reso possibile l’ottenimento di risultati altrimenti insperati.
Il metodo che abbiamo scelto di presentare nella nostra trattazione è chiamato metodo WKB , o approssimazione semi-classica, e prende il nome dai fisici
Wentzel[3], Kramers[4] e Brillouin[5] che lo svilupparono nel 1926. Tale metodo
ci permette di risolvere un problema molto comune in meccanica quantistica, cioè
quello del comportamento delle particelle atomiche e subatomiche in presenza di un
potenziale elettromagnetico. Di per sé questa classe di problemi va già incontro a
1
2
CAPITOLO 1. INTRODUZIONE
modellizzazioni “brutali”, quali possono essere per esempio le buche di potenziale
quadrate o le barriere di potenziale rettangolari. Ciò nonostante i risultati ottenuti
sono perfettamente esatti. Questo purtroppo non è possibile nel caso in cui il potenziale del nostro sistema sia non costante a tratti; in casi come questo si ricorre
al metodo di approssimazione WKB per giungere ad una soluzione il più possibile vicina a quella esatta. In realtà il metodo di approssimazione delle equazioni
differenziali del secondo ordine era noto già nel 1923, essendo stato sviluppato dal
matematico Harold Jeffreys[2], tant’è che in alcuni casi tale approssimazione prende
il nome di WKBJ (o JWKB in Inghilterra). Poiché però l’equazione di Schrödinger
venne sviluppata solo tre anni più tardi e Wentzel, Kramers e Brillouin erano ignari
di questo lavoro, il nome di Jeffreys viene spesso omesso.
Inizieremo quindi la nostra trattazione introducendo i modelli più semplici, quali
la buca di potenziale quadrata e la barriera di potenziale rettangolare, per poi passare ai casi con potenziale non costante a tratti per i quali ricorreremo al metodo di
approssimazione WKB. Infine useremo tale metodo per trattare il caso dell’urto tra
un deutone ed un nucleo pesante .
1.1
Cenni preliminari
Si consideri una particella quantistica in moto in un potenziale non dipendente dal
tempo, V (x). L’equazione di Schrödinger per questo caso è data da
i~
~2 d2
∂
Ψ(x, t) = −
Ψ(x, t) + V (x)Ψ(x, t)
∂t
2m dx2
In quanto l’hamiltoniana non dipende dal tempo, la dipendenza temporale della
funzione d’onda può essere fattorizzata, ottenendo
Ψ(x, t) =
X
i
AE e− ~ Et ψE (x)
E
che possiamo utilizzare per studiare il problema agli autovalori
HψE (x) = EψE (x)
1.2. BUCA RETTANGOLARE SIMMETRICA
3
Figura 1.1:
dalla cui formula, sostituendo ad H la sua forma estesa otteniamo l’equazione di
Schrödinger stazionaria
"
#
~2 d2
−
+ V (x) ψ(x) = Eψ(x)
2m dx2
che è l’equazione dalla quale partiremo per studiare i nostri esempi[1].
1.2
Buca rettangolare simmetrica
Il primo esempio che proponiamo è quello della buca rettangolare simmetrica (fig.
1.1), modello che ci permette di trattare con una certa precisione una serie di problemi realistici, come per esempio le giunzioni PNP o NPN nei semiconduttori, in
quanto modellizza abbastanza bene cosa accada in presenza di potenziali attrattivi
generici.
Consideriamo quindi un potenziale definito da:
V (x) =




0
per |x| ≤ L



V0
per |x| > L
con V 0 costante positiva. In questo modo ci troviamo a lavorare con un potenziale
pari, infatti V (x) = V (−x), quindi per il teorema della parità avremo soluzioni di
parità definita, saranno quindi o pari o dispari.
Dovremo adesso procedere con lo studio dei possibili stati legati e successivamente degli stati del continuo.
4
CAPITOLO 1. INTRODUZIONE
1.2.1
Stati legati
Nello studio degli stati legati cerchiamo gli autovalori dell’energia per i quali si ha
0 < E < V0 , ovvero quelli che classicamente si troverebbero all’interno della buca
stessa.
Sappiamo inoltre che le autofunzioni di H saranno anche autofunzioni dell’operatore
parità, poiché questi due commutano nell’intorno di zero, e questo comporta che
avremo soluzioni di parità definita.
Il primo passo da effettuare nel nostro procedimento è quello di separare lo spazio in
tre regioni, per poi risolverne le relative equazioni di Schrödinger indipendenti dal
tempo, ed infine imporre la continuità delle autofunzioni e delle loro derivate prime
nei punti “critici” del nostro modello, ovvero ad x = −L ed x = L, analizzando
separatamente il caso pari e quello dispari.
Lo spazio verrà suddiviso nel seguente modo
x = (−∞, −L)
regione 1
x = (−L, +L)
regione 2
x = (+L, +∞)
regione 3
le cui equazioni di Schrödinger saranno date da
d2 ψ 2m(V0 − E)
−
ψ=0
dx2
~2
d2 ψ 2mE
+ 2 =0
dx2
~
per le regioni 1 e 3
per la regione 2
che diventano
ψ 00 − η 2 ψ = 0
ψ 00 + k 2 ψ = 0
dove sono stati posti
per le regioni 1 e 3
per la regione 2
5
1.2. BUCA RETTANGOLARE SIMMETRICA
q
η=
2m(V0 − E)
√
,
k=
~
2mE
~
Le soluzioni generali delle equazioni di Schrödinger saranno
ψ1 (x) = Ceηx + De−ηx
ψ2 (x) = A cos kx + B sin kx
ψ3 (x) = F eηx + Ge−ηx
Il nostro obiettivo è ora quello di trovare gli stati legati del sistema, escluderemo
quindi tutte le soluzioni divergenti, mantenendo quelle che si annullano per x → ±∞.
Ciò comporta che D = F = 0.
Successivamente procederemo trattando separatamente il caso pari e quello dispari,
imponendo la continuità delle funzioni d’onda sopra elencate, e delle relative derivate
prime, in x = L. Per x = −L il procedimento sarà analogo per simmetria .
Questo procedimento ci porterà ad avere
cot kL =
k
>0
η
per il caso pari
tan kL = −
k
<0
η
per il caso dispari
le quali diseguaglianze sono date dal fatto che k ed η sono definite positive. Successivamente introduciamo la costante
ξ = kL
con la quale, elevando al quadrato le equazioni ottenute precedentemente e sostituendovi i valori di k ed η, troviamo che
cos2 ξ =
E
V0
per il caso pari
6
CAPITOLO 1. INTRODUZIONE
sin2 =
E
V0
per il caso dispari
A questo punto ricordando che
E
~2 k 2
~2 (kL)2
~2
=
=
=
ξ2
2
2
V0
2mV0
2mV0 L
2mV0 L
2
~
dove per comodità possiamo inserire la costante α2 = 2mV
2 , otteniamo i seguenti
0L
risultati
cos2 = α2 ξ 2
sin2 = α2 ξ 2
per il caso pari
per il caso dispari
A questo punto dovremo solo estrarre le radici quadrate, eliminando le radici spurie
dovute alle condizioni imposte dalle diseguaglianze ottenute precedentemente. In
questo modo otterremo
cos ξ = ±αξ
sin ξ = ±αξ
con la condizione cot ξ > 0
con la condizione tan ξ < 0
per il caso pari
per il caso dispari
E quindi i valori permessi di ξ saranno
kπ < ξ < (2k + 1)
(2k − 1)
π
2
π
< ξ < kπ
2
con k = 0, 1, 2, ... per il caso pari
con k = 1, 2, 3, ... per il caso dispari
Le equazioni trascendenti ottenute sono però solitamente di difficile risoluzione e
quindi se ne cercano solamente le soluzioni numeriche. Piuttosto che la soluzione
numerica però, quello che ci interessa conoscere è se il sistema ammette degli stati e
legati, ed eventualmente il loro numero. Un modo di procedere è quello di tracciare
i grafici delle curve cos ξ e ± αξ per il caso pari e sin ξ e ± αξ per il caso dispari.
7
1.2. BUCA RETTANGOLARE SIMMETRICA
Le intersezioni retta-curva, non saranno altro che i nostri stati legati.
Da questa rappresentazione grafica si osserva facilmente che per buche poco
profonde e molto larghe, ovvero quando α < π2 , possiamo non avere soluzioni
dispari, ma avremo comunque una soluzione pari. Dunque indipendentemente dal
valore di α, la buca avrà sempre uno stato legato, e anche in caso di più stati legati,
il primo sarà sempre pari. Inoltre le soluzioni saranno sempre alternativamente pari
e dispari, e sempre in numero finito.
Per trovare i valori dell’energia per i diversi livelli energetici, dovremo sostituire una soluzione delle equazioni trascendenti, che chiameremo ξn , nelle definizioni
precedenti, ricavando i valori del parametri
ξn
kn =
L
q
,
ηn =
2m(V0 − En )
~
dai quali ricaviamo i valori delle varie energie
En =
~2 2
ξ
2mL2 n
Grazie alla continuità in x = L, fissando le costanti della soluzione generale, otterremo infine le autofunzioni
C = A cos kn L · eηn L
C = B sin kn L · eηn L
per il caso pari
per il caso dispari
dove A e B sono delle costanti determinate dalla normalizzazione.
1.2.2
Stati del continuo
Analizziamo ora gli stati per i quali E > V0 , cioè quelli per i quali, secondo l’analisi
classica, non avremmo la presenza di stati legati. Quello che cercheremo saranno
infatti i coefficienti di riflessione e di trasmissione, ovvero la probabilità che la
particella, che immagineremo proveniente da x = −∞ e con un impulso pari ad ~q,
ha di essere riflessa dal potenziale o di attraversarlo.
8
CAPITOLO 1. INTRODUZIONE
Dividiamo lo spazio nelle tre regioni usate per il caso con E < V0 , le equazioni di
Schrödinger per questo caso diventeranno
ψ 00 + q 2 ψ = 0
ψ 00 + k 2 ψ = 0
per le regioni 1 e 3
per la regione 2
dove abbiamo posto
q
q=
2m(E − V0 )
,
~
√
2mE
k=
~
le cui soluzioni sono
ψ1 (x) = Aeiqx + Be−iqx
ψ2 (x) = Ceikx + De−ikx
ψ3 (x) = F eiqx + Ge−iqx
Avendo preso in esame una particella proveniente da x = −∞sceglieremo come
condizione iniziale G = 0. Successivamente, come nel caso precedente calcoleremo
le derivate prime delle equazioni di Schrödinger e ne imporremo la continuità in
x = ±L. I nostri coefficienti saranno dati da
V02 sin2 2qL
|B|2
=
1
+
T =
|A|2
4E(E + V0 )
!−1
|F |2
4E(E + V0 )
R=
= 1+ 2 2
2
|A|
V0 sin 2qL
!−1
Quello che si nota è che ovviamente R + T = 1, ed inoltre, quando sin 2qL = 0,
nπ
ovvero quando l’impulso q della particella sarà pari a 2L , il coefficiente T sarà
uguale ad 1, avremo quindi la trasmissione totale dell’onda incidente. Le energie
che avranno questi stati a trasmissione totale saranno date da
En =
~2 qn2
~2 π 2
− V0 =
− V0
2m
8mL2
1.3. BARRIERA DI POTENZIALE ED EFFETTO TUNNEL
9
Figura 1.2:
che vengono identificati come livelli virtuali, e possono essere visti come una sorta
di continuazione dei livelli discreti della buca, i cui corrispondenti stati vengono
chiamati stati virtuali.
1.3
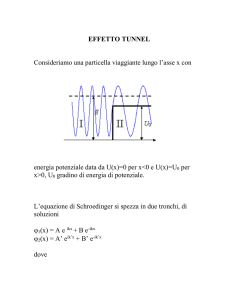
Barriera di potenziale ed effetto tunnel
Il secondo ed ultimo esempio che trattiamo è quello della barriera di potenziale,
che può essere visto in un certo senso come l’opposto del problema della buca di
potenziale (fig. 1.2). In questo caso infatti la forma del nostro potenziale sarà
V (x) =




0
per |x| > L



V0
per |x| ≤ L
dove V0 > 0. La geometria stessa del nostro problema ci suggerisce che non sarà
possibile avere stati legati, e che quindi dovremo studiare i coefficienti di trasmissione
e di riflessione per le onde incidenti.
Dovremmo adesso procedere separando i due casi in cui l’onda incidente abbia
energia E maggiore o minore del del potenziale V0 . Va da sé però, che il caso E > V0
non costituisce una novità rispetto al caso della buca di potenziale, avremo infatti
dei coefficienti di trasmissione e riflessione parziale delle onde, che verranno calcolati
seguendo lo stesso procedimento matematico. Il caso interessante è quello in cui
E < V0 . Analizzato in maniera classica infatti, questo problema darebbe luogo ad
una riflessione totale dell’onda da parte della barriera di potenziale, poiché l’energia
10
CAPITOLO 1. INTRODUZIONE
della particella, minore di quella del potenziale, non permetterebbe a quest’ultima
di procedere oltre. Vedremo però che il risultato a cui giungeremo sarà ben diverso.
Procediamo dividendo lo spazio in tre regioni, come fatto per il caso della buca di
potenziale
x = (−∞, −L)
regione 1
x = (−L, +L)
regione 2
x = (+L, +∞)
regione 3
Le equazioni di Schrödinger per le tre regioni saranno le seguenti
ψ 00 + k 2 ψ = 0
per le regioni 1 e 3
ψ 00 − η 2 ψ = 0
per la regione 2
dove abbiamo sostituito
√
k=
2mE
~
q
,
η=
2m(V0 − E)
~
Anche in questo caso prendiamo una particella incidente proveniente da x = −∞,
ci ritroveremo ad avere quindi come soluzioni delle funzioni oscillanti per le regioni
1 e 3, e delle soluzioni esponenzialmente smorzate per la regione 2
ψ1 (x) = Aeikx + Be−ikx
ψ2 (x) = Ceηx + De−ηx
ψ3 (x) = F eikx
Come nel caso della buca di potenziale procediamo adesso calcolando le derivate
prime delle soluzioni, e imponendo la continuità in x = ±L. Così facendo potremo
giungere al valore dei coefficienti di trasmissione e di riflessione, che saranno dati da
R=
(1 + σ 2 )2 sinh 2ηL
4σ 2 + (1 + σ 2 )2 sinh2 2ηL
1.3. BARRIERA DI POTENZIALE ED EFFETTO TUNNEL
T =
11
4σ 2
4σ 2 + (1 + σ 2 )2 sinh2 2ηL
dove è stato posto
σ2 =
η2
V0 − E
=
2
k
E
Come vediamo, il risultato ottenuto è ben diverso da quello che ci si aspetterebbe
seguendo le leggi della fisica classica, ci troviamo infatti ad avere una particella che
supera una barriera di potenziale pur non avendo l’energia per farlo. Questo fenomeno è noto col nome di effetto tunnel, ed è probabilmente il fenomeno quantistico
più sfruttato nel campo delle applicazioni tecnologiche. Molti oggetti di uso quotidiano nell’ambito tecnologico utilizzano infatti il principio di tale teoria, come ad
esempio le memorie flash dei dispositivi elettronici, alcuni particolari tipi di diodi, i
microscopi ad effetto tunnel e molti altri ancora.
12
CAPITOLO 1. INTRODUZIONE
Capitolo 2
L’approssimazione WKB
L’idea che sta alla base di tale teoria è la seguente: immaginiamo, come nei casi
presentati nell’introduzione, di avere una particella quantistica, avente energia E,
che si muove in una regione dove è presente un potenziale costante V (x). Se E > V ,
come abbiamo visto precedentemente, la funzione d’onda sarà data da
ψ(x) = Ae±ikx
dove è stato posto
q
k=
2m(E − V )
~
Come nei casi precedenti, il segno più all’esponenziale indica che la particella viaggia
verso destra, e il segno meno che viaggia verso sinistra. In questo caso la funzione
d’onda sarà ovviamente oscillatoria, con lunghezza d’onda costante, pari a λ = 2π/k,
e ampiezza A anch’essa costante. Supponiamo adesso che il nostro potenziale non
sia costante, ma varii in modo piuttosto lento rispetto a λ, così da poter essere
considerato costante in una regione di grandezza pari a svariate λ. In questo modo
la nostra funzione d’onda potrà essere comunque considerata sinusoidale, con l’eccezione che l’ampiezza e la lunghezza d’onda varieranno lentamente con x. Avremo
quindi in questo caso una sorta di doppia dipendenza da x.
Allo stesso modo, se E < V , con V costante, la nostra funzione d’onda sarà
ψ(x) = Ae±kx
13
14
CAPITOLO 2. L’APPROSSIMAZIONE WKB
con
q
k=
2m(V − E)
~
Se V (x) non è costante, ma varia lentamente rispetto a 1/k, la soluzione rimarrà
praticamente esponenziale, ma con delle lente variazioni di A e k in funzione di x.
Il punto critico di tale teoria si ha però in corrispondenza dei punti d’inversione
del moto della particella, cioè quando E ∼ V . Qui λ( o 1/k) tenderà ad infinito,
e la variazione di V (x) non sarà ovviamente sufficientemente lenta. Come vedremo
questa sarà la parte più difficile da sviluppare, sebbene i risultati cui si giungerà
saranno relativamente semplici da implementare[7].
2.1
Il caso “classico”
Il caso che analizzeremo adesso è quello per il quale E > V (x), noto anche con il
nome di caso classico, poiché per ovvie ragioni, nella trattazione classica di questo
tipo di problemi la particella è confinata nella regione in cui E > V (x).
Partiamo dall’equazione di Schrödinger
−
~2 d2 ψ
+ V (x)ψ = Eψ
2m dx2
che riscriveremo in questo caso come
d2 ψ
p2
=
−
ψ
dx2
~2
dove abbiamo posto
p(x) =
q
2m(E − V (x))
La ψ è generalmente una funzione complessa, che possiamo scrivere in termini di
ampiezza e fase, sarà quindi del tipo
ψ(x) = Aeiφ(x)
15
2.1. IL CASO “CLASSICO”
Calcoliamone adesso la derivata prima e seconda rispetto ad x
dψ
= (A0 + iAφ0 ) eiφ
dx
d2 ψ 00
0 0
00
0 2
=
A
+
2iA
φ
+
iAφ
−
A
(φ
)
dx2
ed inseriamole nell’equazione di Schrödinger riscritta. Avremo quindi
2
A00 + 2iA0 φ0 + iAφ00 − A (φ0 ) = −
p2
A
~2
che può essere separata separata in due equazioni, una per la parte reale e una per
la parte immaginaria. Avremo perciò
2
A00 − A (φ0 ) = −
2A0 φ0 + Aφ00 = 0
p2
A
~2
per la parte reale
per la parte immaginaria
Queste equazioni sono equivalenti all’equazione di Schrödinger iniziale, e quella per
la parte immaginaria è facilmente risolvibile. La soluzione sarà
C
A= √ 0
φ
dove C è una costante reale. Quella relativa alla parte reale tuttavia non può essere
generalmente risolta, ed è in questo punto che viene introdotta la teoria dell’approssimazione WKB.
Come sappiamo infatti l’ampiezza A varia molto lentamente, e in questo modo il
termine A00 /A diventa trascurabile rispetto ai termini (φ0 )2 e p2 /~2 . Questa non è
altro che la nostra condizione necessaria all’applicazione del metodo WKB, che si
traduce in modo generalizzato | dλ
| 1, detta condizione di semi-classicità, e ci
dx
dice che la lunghezza d’onda della nostra particella deve variare poco su distanze
dell’ordine della sua lunghezza per far sì che il nostro metodo di approssimazione
16
CAPITOLO 2. L’APPROSSIMAZIONE WKB
sia efficace. A questo punto la nostra equazione diventa semplicemente
p2
(φ ) = 2
~
0 2
che ci dà come risultato
1
φ(x) = ±
~
p(x)dx
dove gli estremi d’integrazione verranno definiti dalla geometria del problema in
esame.Ne segue perciò che
C 2 ± i p(x)dx
e ~
ψ(x)2 ∼
=
p(x)
e la soluzione generale, ovvero quella approssimata, dell’equazione di Schrödinger
sarà data dalla combinazione delle due soluzioni, ovvero quella con l’esponente negativo e quella con l’esponente positivo.
Un’altra osservazione che possiamo fare è che prendendo in esame la probabilità di
trovare la particella in un determinato punto x del nostro spazio, ovvero
|C|2
|ψ(x)|2 ∼
=
p(x)
si può notare come questa sia inversamente proporzionale al relativo impulso, inteso
in maniera classica, in quel punto. Ciò è esattamente quello che ci si aspetta, infatti
più una particella si muove rapidamente, minore sarà la probabilità di trovarla in
un punto prefissato. Questa osservazione “semiclassica” può essere anch’essa usata
come punto chiave per uno sviluppo dell’approssimazione WKB, alternativo al nostro. In questo caso si avrebbe più chiaro l’aspetto puramente fisico della teoria, ma
il nostro sviluppo è matematicamente più “pulito”.
Procediamo adesso presentando un esempio, molto simile a quello della buca rettangolare simmetrica, ovvero una buca con pareti verticali rette, ma fondo irregolare,
e verifichiamo la bontà del metodo di approssimazione per questo caso.
17
2.1. IL CASO “CLASSICO”
Figura 2.1:
2.1.1
Buca di potenziale con fondo irregolare
Nell’esempio che andiamo ad analizzare il nostro potenziale sarà rappresentato da




f (x)
per 0 < x < L


+∞
per x < 0 , x > L
V (x) = 
dove f(x) è una funzione data dal problema specifico, che descrive la forma del potenziale (fig. 2.1). Posizioniamoci ora all’interno della buca, e assumiamo ovviamente
E>V(x). Usando il metodo presentato precedentemente, giungiamo alla soluzione
dell’equazione di Schrödinger, che sarà pari a
1
ψ(x) ∼
[C1 sin φ(x) + C2 cos φ(x)]
=q
p(x)
dove, come già visto in precedenza
1
φ(x) =
~
x
p(x0 )dx0
0
Adesso, come nel caso della buca rettangolare “classica”, dobbiamo imporre che la
nostra funzione d’onda si annulli agli estremi della buca, per x=0 e di conseguenza
φ = 0, avremo cheC2 = 0. Per x = L avremo invece
φ(L) = nπ
con n = 1, 2, 3...
18
CAPITOLO 2. L’APPROSSIMAZIONE WKB
Il risultato al quale giungiamo è quindi la nostra condizione di quantizzazione, che
determinerà le energie permesse in maniera approssimata, e sarà data da
L
p(x)dx = nπ~
0
2.2
Barriera di potenziale ed effetto tunnel
Ci occuperemo adesso del caso in cui E < V , il cui procedimento, pressoché identico
a quello per E > V , ci darà come risultato per la funzione d’onda
1
C
ψ(x) ∼
e± ~ |p(x)|dx
=q
|p(x)|
Consideriamo adesso come esempio, una barriera di potenziale simile alla precedente, ma con la superficie superiore irregolare (fig. 2.2).
Figura 2.2:
In questo caso il nostro potenziale avrà quindi questa forma
V (x) =




0
per x > L, x < 0



f (x)
per 0 < x < L
dove, come per il caso della buca, f (x) è data dal caso specifico. Anche in questo
2.2. BARRIERA DI POTENZIALE ED EFFETTO TUNNEL
19
caso lo spazio verrà diviso in tre regioni
x = (−∞, 0)
regione 1
x = (0, L)
regione 2
x = (L, +∞)
regione 3
Le cui relative equazioni di Schrödinger saranno
ψ 00 + k 2 ψ = 0
ψ 00 = −
per le regioni 1 e 3
|p(x)|
ψ
~2
per la regione 2
dove, come già visto
√
k=
2mE
~
p(x) =
,
q
2m(E − V (x))
Le nostre soluzioni saranno date da
ψ1 (x) = Aeikx + Be−ikx
1
C
ψ2 (x) ∼
e~
=q
|p(x)|
x
0
|p(x0 )dx0
1 x
D
0
0
+q
e− ~ 0 |p(x )dx
|p(x)|
ψ3 (x) = F eikx
E saranno ottenute, per quanto riguarda le regioni 1 e 3, nel medesimo modo che per
la barriera rettangolare, mentre verrà usata l’approssimazione WKB per la regione
2.
Quello che ci riguarda, ovvero il coefficiente di trasmissione, come nella barriera
precedente, sarà dato dal rapporto
T =
|F |2
|A|2
Se però la buca sarà particolarmente alta o larga, con un conseguente calo della
probabilità di tunneling, il coefficiente C decrescerà sensibilmente, creando nella
20
CAPITOLO 2. L’APPROSSIMAZIONE WKB
funzione d’onda una sorta di stallo, facendo decrescere a sua volta l’ampiezza dell’onda incidente. Le ampiezze relative dell’onda incidente e di quella trasmessa
saranno quindi determinata dalla diminuzione del valore dell’esponenziale rimasto
nella regione 2
1 L
|F |
0
0
∼ e− ~ 0 |p(x )dx
|A|
e il coefficiente di trasmissione sarà perciò
T ∼
= e−2γ
2.3
1
con γ =
~
L
|p(x)|dx
(2.1)
o
Le formule di connessione
Finora negli esempi che abbiamo trattato, abbiamo sempre assunto che i “muri” delle buche, o barriere, di potenziale fossero verticali, così che le condizioni al contorno
fossero banali, e le soluzioni semplici da ottenere. Vedremo anche che i risultati
ottenuti saranno accettabili fintanto che i bordi del nostro potenziale non saranno
troppo ripidi. È tuttavia di notevole interesse studiare il comportamento della funzione d’onda della nostra particella in un punto d’inversione, ovvero quando E = V ,
situazione in cui l’approssimazione WKB stessa non è sufficiente per ottenere dei
risultati soddisfacenti.
Tratteremo adesso il problema per gli stati legati, e per prima cosa, assumeremo
che il nostro potenziale sia definito in modo tale da avere il punto di inversione
destro coincidente con x = 0, così da facilitarci i calcoli. Seguendo i procedimenti
elencati precedentemente avremo che




1

√
h


1

√
De− ~
ψ(x) ∼
=
p(x)
|p(x)|
i
Be ~
0
x
1
p(x0 )dx0
x
0
i
+ Ce− ~
|p(x0 )dx0
0
x
p(x0 )dx0
i
per x < 0
per x > 0
Assumiamo inoltre che V (x) > E per x > 0, in modo tale da poter eliminare l’esponenziale positivo per questa regione, in quanto divergente a +∞. Dobbiamo
adesso trovare le condizioni al contorno, ma, come accennato in precedenza, l’ap-
21
2.3. LE FORMULE DI CONNESSIONE
prossimazione WKB non ci è sufficiente. Per x = 0, punto di inversione del moto
e quindi avente p (x) = 0 infatti ψ diverge a +∞, cosa che ovviamente non accade alla funzione d’onda reale. Il problema diventerebbe quindi irrisolvibile, poiché
senza le condizioni al contorno non è possibile trovare le energie permesse. Quello
che dovremo fare a questo punto è unire le due soluzioni ottenute col metodo WKB,
usando una funzione d’onda di raccordo, che copre il punto x = 0 e il suo intorno.
Dato che analizzeremo solo l’intorno di x = 0, il nostro potenziale potrà essere
approssimato ad una retta, così da avere
V (x) ∼
= E + V 0 (0) x
La nostra equazione di Schrödinger diventerà quindi
−
~2 d2 ψp
+ (E + V 0 (0) x) ψp = Eψp
2
2m dx
o, in altra forma
d2 ψp
= α3 xψp
2
dx
dove è stato posto
α=
1/3
2m
V (0)
~2
Possiamo inoltre introdurre una variabile indipendente, z, definita come
z = αx
in modo tale che la nostra funzione diventi
d2 ψp
= zψp
dz 2
Questo tipo di equazioni è noto col nome di Equazione di Airy, e le relative soluzioni
sono le Funzioni di Airy. In quanto equazione differenziale del secondo ordine,
avremo due funzioni di Airy linearmente indipendenti, Ai(z) e Bi(z), e la soluzione
generale dell’equazione sarà data dalla loro combinazione lineare. A questo punto è
22
CAPITOLO 2. L’APPROSSIMAZIONE WKB
semplice prevedere che la nostra funzione di raccordo sarà data da
ψp (x) = aAi (αx) + bBi (αx)
con a e b costanti appropriate.
La ψp sarà quindi la nostra funzione d’onda (approssimata), per l’intorno di x = 0.
Il nostro obiettivo è adesso quello di “unirla” alle soluzioni ottenute col metodo
WKB nelle regioni di sovrapposizione per l’intorno destro e sinistro di x = 0. Per
far sì che questo metodo funzioni, le regioni di sovrapposizione dovranno essere
abbastanza vicine al punto d’inversione, così che il nostro potenziale linearizzato
rimanga ragionevolmente accurato, ma lontane abbastanza da rendere accettabili le
soluzioni ottenute col metodo WKB.
Nelle regioni di sovrapposizione quindi avremo che
p(x) ∼
=
q
√
3
2m (E − E − V 0 (0) x) = ~α /2 −x
e in particolare nella regione relativa all’intorno destro di x = 0,
x
|p(x )|dx ∼
= ~α
0
0
x
3/2
0
0
√
2
3
x0 dx0 = ~(αx) /2
3
così che la nostra funzione d’onda WKB per x > 0 potrà essere riscritta in questo
modo
ψ(x) ∼
=√
3
D
− 23 (αx) /2
e
~α3/4 x1/4
Frattanto , usando la forma asintotica per delle funzioni di Airy per valori di z molto
grandi, la nostra funzione di raccordo per l’intorno destro di x = 0 diventerà
3/2
3/2
2
2
a
b
e− 3 (αx) + √
e 3 (αx)
ψp (x) ∼
= √
1/4
1/4
2 π(αx)
π(αx)
Confrontando le due soluzioni troviamo che
s
a=
4π
D
α~
,
b=0
23
2.3. LE FORMULE DI CONNESSIONE
Ripetiamo ora la procedura per la regione relativa all’intorno sinistro di x = 0.
In questo caso avremo, poiché x < 0,
0
2
3
p(x0 )dx0 ∼
= ~(−αx) /2
3
x
e la nostra funziona d’onda WKB sarà adesso
ψ(x) ∼
=√
3
3
1
i 23 (−αx) /2
−i 32 (−αx) /2
Be
+
Ce
~α3/4 (−x)1/4
A questo punto, come in precedenza useremo la forma asintotica delle funzioni di
Airy, ma questa volta per z molto grandi, ma negativi. La funzione di raccordo sarà
3/2
2
2
a
a
π
1 iπ/4 i 2 (−αx)3/2
3
π
=√
e e3
sin (−αx) /2 +
− e−i /4 e−i 3 (−αx)
ψp (x) ∼
=√
1/4
1/4
π(−αx)
3
4
π(−αx) 2i
dove è stato ovviamente posto b = 0 per via del risultato precedentemente ottenuto.
Confrontando le funzioni d’onda il risultato che otteniamo è
B
a
√ eiπ/4 = √
2i π
~α
−a −iπ/4
C
√ e
=√
2i π
~α
,
che possono essere riscritte nella seguente forma
B = −iei /4 D
π
,
C = ie−i /4 D
π
e son le cosiddette formule di connessione. Quello che ci rimane da fare adesso non
è altro che riscrivere le funzioni d’onda WKB inserendo la costante normalizzata D,
e traslando il punto d’inversione da x = 0 ad un punto arbitrario x2 , così da ottenere
le seguenti espressioni




2D

√
sin


D

√
e
ψ(x) ∼
=
p(x)
|p(x)|
h 1 x2
− ~i
~
x
x2
x
p(x0 )dx0 +
|p(x0 )|dx0
π
4
i
per x < x2
per x > x2
24
2.3.1
CAPITOLO 2. L’APPROSSIMAZIONE WKB
Buca di potenziale con pareti curve
Figura 2.3:
Le equazioni appena ottenute raccordano le equazioni WKB nella regione in cui
il potenziale ha inclinazione positiva, ma procedendo allo stesso modo possiamo
facilmente trovare le equazioni per un potenziale discendente




D0

√
e− ~


2D0

√
sin
ψ(x) ∼
=
1
|p(x)|
p(x)
x
x
1
|p(x0 )|dx0
per x < x1
h 1 x
~
p(x0 )dx0 +
x1
π
4
i
per x > x1
Quindi prendendo in esame il caso di una buca di potenziale con le pareti curve (fig.
2.3), la funzione d’onda nella regione interna della buca, ovvero dove x1 < x < x2 ,
potrà essere scritta come
2D
ψ(x) ∼
sin θ2 (x)
=q
p(x)
1
con θ2 (x) =
~
x2
p(x0 )dx0 +
x
π
4
ma anche come
−2D0
ψ(x) ∼
sin θ1 (x)
=q
p(x)
1
con θ1 (x) = −
~
x
p(x0 )dx0 +
x1
π
4
a seconda che si parta dalle equazioni per x < x2 , o da quelle per x > x1 . Evidentemente l’argomento del seno dovrà essere uguale per le due funzioni d’onda, a meno
di π. Si dovrà avere cioè θ2 = θ1 + nπ, e da ciò segue che
x2
p(x)dx = n −
x1
1
π~
2
con n = 1, 2, 3...
2.3. LE FORMULE DI CONNESSIONE
25
Questa condizione di quantizzazione determina quindi le energie permesse per una
buca di potenziale con le pareti curve. Quello che salta all’occhio è che l’unica differenza che abbiamo con la formula per la buca di potenziale “quadrata”, consiste nel
termine 12 , che nella buca quadrata manca. Inoltre, sapendo che l’approssimazione
WKB è più consistente nella trattazione “semiclassica” dei problemi, e quindi per n
molto grandi, ci rendiamo conto di quanto la differenza sia più nella forma che nella
sostanza. Ad ogni modo il risultato ottenuto è di grande utilità, in quanto ci permette di trovare le energie permesse dal sistema analizzando solamente un integrale,
e quindi tralasciando l’intera funzione d’onda.
26
CAPITOLO 2. L’APPROSSIMAZIONE WKB
Capitolo 3
L’approssimazione WKB in un
campo a simmetria centrale
Dopo aver studiato il metodo di approssimazione WKB nei casi lineari ci apprestiamo adesso ad analizzarlo per un una particella che compie un moto in un campo a
simmetria centrale. Introdurremo il metodo di approssimazione per il caso generale,
e successivamente lo applicheremo al problema che abbiamo scelto di presentare.
L’equazione di Schrödinger indipendente dal tempo per il caso in esame sarà
~2
−
2m
2 ∂
L2
∂2
+
ψ(r,
θ,
φ)
+
ψ(r, θ, φ) + V (r) ψ(r, θ, φ) = Eψ(r, θ, φ)
∂r2 r ∂r
2mr2
!
che come sappiamo, sfruttando l’indipendenza delle variabili, potrà essere divisa in
due equazioni indipendenti, una relativa alla parte radiale e l’altra a quella angolare.
Per la parte radiale si avrà
~2
−
2m
!
d2
2 d
~2 l(l + 1)
+
ϕ(r)
+
V
(r)ϕ(r)
−
= Eϕ(r)
dr2 r dr
2mr2
(3.1)
mentre per quella radiale
L2 Y (θ, φ) = λY (θ, φ)
che riconosciamo essere l’equazione agli autovalori per l’operatore L2 , le cui autofunzioni sono le armoniche sferiche, e la cui degenerazione è risolta affiancando
l’operatore L3 , che commuta con L2 e con l’hamiltoniana.
27
28CAPITOLO 3. L’APPROSSIMAZIONE WKB IN UN CAMPO A SIMMETRIA CENTRALE
Nel problema che andremo ad analizzare però, la parte angolare dell’equazione di
Schrödinger non entrerà in gioco, ci limiteremo quindi per completezza a fornire
solamente i risultati relativi all’applicazione del metodo di approssimazione WKB
per il caso con numero quantico magnetico nullo (m = 0), essendo questo il caso
più importante e frequente nelle applicazioni pratiche. L’armonica sferica trovata
mediante il metodo di approssimazione sarà dunque
l
i
Yl0 (θ, φ) ∼
=
π
h
l + 12 θ +
√
sin θ
π
4
i
Passiamo adesso allo studio della parte radiale dell’equazione. L’equazione (3.1)
può essere riscritta come
!
d2 ϕl 2 dϕl
+
dr2
r dr
2m [E − V (r)] l(l + 1)
−
ϕl = 0
~2
r2
che non è altro che un’equazione differenziale omogenea del secondo ordine. Il pedice apposto a ϕ indica che l’equazione, e di conseguenza la soluzione, dipenderà
dal valore di l. Ridefinendo adesso la funzione ϕl (r) = χl /r, possiamo riscrivere
l’equazione precedente come
−
~2 d2
(l)
χl (r) + Vef f (r)χl (r) = Eχl (r)
2
2m dr
(3.2)
dove abbiamo posto
(l)
Vef f (r) = V (r) +
~l(l + 1)
2mr2
e cioè la somma del potenziale centrale e di quello centrifugo, dovuto al momento
angolare orbitale della particella. L’equazione (3.2) adesso non è altro che un’equazione di Schrödinger stazionaria unidimensionale nella variabile r; vi saranno quindi
applicate le considerazioni fatte per i potenziali unidimensionali, tenendo però conto
della presenza del termine centrifugo, che complicherà la forma del potenziale.
Partiamo col prendere in esame il caso più semplice, ovvero quello con il termine
l = 0; va da sé che con l’azzerarsi del termine l la forma del potenziale diventa
identica a quella del potenziale lineare, e se quindi V (r) soddisfa la condizione di
29
semi-classicità, la funzione d’onda χl approssimata sarà determinata in conformità
con le formule ricavate per il caso lineare, con l’unica, ovvia differenza, che il raggio
r sarà sempre maggiore di zero.
Se viceversa l 6= 0, la condizione di semi-classicità dovrà essere soddisfatta,
oltre che da χl , anche dall’energia centrifuga. Nell’ordine dei piccoli valori di r, il
termine dominante diventa quello dell’energia centrifuga, e la condizione di semiclassicità ci dice che l 1 affinché l’approssimazione sia accettabile. Inoltre si può
facilmente verificare che otterremo il valore corretto della fase della funzione d’onda
χl (r) se la calcoleremo secondo le formule del moto unidimensionale, sostituendo
(l)
però nell’energia potenziale Vef f (r) il coefficiente (l + 21 )2 al posto di l(l + 1), in
modo che il nostro potenziale diventi
2
(l)
Vef f (r) = V (r) +
~
2m
1
2
2
r
l+
2
che può essere visto come un campo coulombiano del tipo V = ±α/r. Dell’intera
regione del moto, quella che ha maggiore importanza per i nostri calcoli è quella
per la quale i valori di r siano tali che |V | ∼ |E|, e cioè r ∼
α
.
|E|
La condizione di
semi-classicità per questo caso si riduce quindi alla richiesta che la lunghezza d’onda
sia piccola rispetto alle dimensioni
α
.
|E|
Questo ci dice perciò che
mα2
|E| 2
~
e cioè il valore assoluto dell’energia deve essere piccolo rispetto all’energia della
particella nel primo livello energetico.
(l)
Analizzando invece la regione delle piccole distanze, ovvero per Vef f (r) E,
scopriamo che non presenta alcun interesse in un campo coulombiano repulsivo,
(l)
poiché per Vef f > E le funzioni d’onda ricavate tramite l’approssimazione WKB
si smorzano esponenzialmente. Se invece ci troviamo in un campo attrattivo, per
valori di l piccoli, è possibile la penetrazione della particella nella regione in cui
(l)
|Vef f | |E|. In questo caso però ci troviamo di nuovo a fronteggiare il problema
dei limiti dell’applicabilità del nostro metodo di approssimazione. Partendo dalla
30CAPITOLO 3. L’APPROSSIMAZIONE WKB IN UN CAMPO A SIMMETRIA CENTRALE
condizione di semi-classicità, vediamo che questa può essere riscritta in un’altra
forma, osservando che
dp
dq
m dV
mF
=
2m(E − V ) = −
=
dx
dx
p dx
p
non è altro che la forza, intesa in senso classico, agente sulla particella
dove F = − dV
dx
nel campo esterno. Introducendo questa forza si ottiene che
m~|F |
1
p3
(3.3)
che ci dice che un’altra condizione necessaria all’applicazione del metodo WKB è
che la quantità di moto della particella sia sufficientemente grande da rendere tale
rapporto molto minore di uno. Usiamo adesso questa condizione per il nostro caso
a simmetria centrale, ponendovi
(l)
dV
α
F = − ef f = − 2
dr
r
il nostro impulso, essendo |U | E potrà essere approssimato a
p≈
q
r
2m|U | ∼
mα
r
che sostituiti nella (3.3) ci danno che
r
~2
mα
Questo ci dice che l’applicabilità del metodo di approssimazione WKB è limitata a
grandi distanze rispetto al raggio della prima orbita per il modello atomico di Bohr.
3.1
L’urto deutone-nucleo pesante
Per concludere la nostra trattazione, mostreremo come l’approssimazione WKB può
essere molto utile per la trattazione di fenomeni ricorrenti nell’ambito astrofisico,
3.1. L’URTO DEUTONE-NUCLEO PESANTE
31
quali possono essere per esempio gli urti tra particelle. La useremo infatti nel nostro
caso per determinare la probabilità di fissione di un deutone nell’urto con un nucleo
pesante.
Per cominciare, considerando l’importante differenza di massa, e quindi di carica,
tra i due nuclei, possiamo considerare il nucleo pesante come il centro fisso di un
campo coulombiano. Sappiamo inoltre che negli urti di questo tipo il contributo
maggiore alla probabilità di reazione è dato dagli urti con momento orbitale nullo,
che nell’approssimazione semi-classica sono considerati frontali, e nei quali il moto
delle particelle si riduce al moto unidimensionale.
Sia ora E l’energia del deutone misurata in unità , energia di legame tra il
protone e il neutrone in esso, ed En e Ep le energie del neutrone e del protone di
fissione, espresse nelle stesse unità. Introduciamo inoltre la coordinata adimensionale
q = r/(Ze2 /), dove Ze è la carica del nucleo, ed indichiamo con q0 il suo valore
nel punto di transizione, cioè nel punto in cui si verifica la fissione del deutone.
Rappresentiamo quindi i valori delle energie nella forma
En =
v2
1
1
vn2
, Ep = p + , E = vd2 +
2
2
qo
q0
dove vn , vp , vd sono le velocità delle particelle nell’istante della fissione, misurate
nelle unità di
q
/m, dove m è la massa del nucleone; vn è reale e coincide con la
velocità del neutrone di fissione, mentre vp e vd saranno complesse. Se applichiamo le
leggi di conservazione dell’energia e della quantità di moto della meccanica classica
nel punto di transizione qo abbiamo che
Ep + En = E − 1,
vp + vn = 2vd
dalle quali si può facilmente ricavare
vp = 2i + vn ,
vd = i + vn ,
1
= E + 1 − vn2 + 2ivn
q0
(3.4)
L’azione del sistema prima della transizione corrisponde al moto del deutone nel
campo del nucleo sino al punto in cui avverrà la fissione, e la sua parte immaginaria
32CAPITOLO 3. L’APPROSSIMAZIONE WKB IN UN CAMPO A SIMMETRIA CENTRALE
sarà
2
r
=S1 = Ze
m
=
v
u
u
t4
q0
−∞
1
E−
q
!
2
r
= Ze
(
)
q
2
m
= 2qo vd − √ arccosh q0 E
E
dove nell’ultima parte sono stati sostituiti i valori ottenuti nella (3.4). Dopo la
transizione l’azione corrisponde al moto del neutrone e del protone a partire dal
punto di fissione, avremo quindi
=S2 = Ze2
2
r
r
= Ze

m 
=

+∞
+∞
vn dq +
qo
qo
(
m
= −vn qo − vp q0 +
s
v
u
u
t2

!

1
Ep −
dq =

q
q
2
arccosh q0 Ep
Ep
)
dove, come per l’equazione precedente abbiamo sostituito i valori delle energie e
delle velocità della (3.4). Ora, secondo la (A.1), sappiamo che la probabilità che si
verifichi il nostro processo è data da
(
2Ze2
ω ∼ exp −
~
r
m
=
"s
q
q
2
2
arccosh q0 Ep − √ arccosh qo E
Ep
E
#)
(3.5)
Dato il carattere esponenziale della dipendenza di ωda En , la probabilità totale
di fissione sarà data dal valore assoluto minimo dell’esponente come funzione di
En (vedi Appendice). Calcoli matematici mostrano che questo valore si ottiene per
En → 0. Di conseguenza dalle definizioni (3.4) deduciamo che qo = 1/(E + 1), e
quindi sostituendo tutto nella (3.5) otteniamo


2Ze2
ω ∼ exp −

~
r
s
m
2
arccos
E−1
s
E−1
2
− √ arccos
E+1
E
s

E 
E+1 
formula che sarà applicabile a patto che il valore dell’esponenziale sia grande rispetto
all’unità (vedi Appendice).
Calcolata la parte immaginaria dell’azione S = S1 + S2 per i valori di En diversi
da zero, si può determinare la distribuzione in funzione dell’energia delle particelle
33
3.1. L’URTO DEUTONE-NUCLEO PESANTE
di fissione. Nell’intorno di En = 0 abbiamo che
=S(En ) − =S(0) ≈ En
d=S
dEn
!
En =0
dalla quale si ricava che

 2Ze2
dω
∼ exp −

dEn
~
r

m 
3−E
1
q
En
arccos
+
(E − 1)(E + 1)2
2(E − 1)3
s

E − 1 
E+1 
che ci dà il valore della probabilità di fissione del deutone nell’urto con il nucleo
pesante.
Come si evince dalla trattazione di questo problema, il metodo di approssimazione WKB si rivela estremamente utile nella risoluzione di problemi legati a fenomeni
fisici altrimenti molto complicati da risolvere. L’esempio da noi proposto rappresenta già buon metro di giudizio, poiché un problema del genere trattato in maniera
rigorosa sarebbe stato di gran lunga più complesso, in quanto nella risoluzione si sarebbero dovuti considerare argomenti che in questo modo vengono completamente
esclusi e che ne avrebbero reso la trattazione molto più problematica.
Non c’è da stupirsi quindi se il metodo di approssimazione WKB sia considerato
come una delle più importanti teorie di tutta la meccanica quantistica, non tanto
per i concetti o per l’innovazione che magari hanno portato altre teorie, quanto più
per l’utilità che presenta e che ci permette di lavorare su fenomeni molto complessi
in maniera relativamente semplice.
34CAPITOLO 3. L’APPROSSIMAZIONE WKB IN UN CAMPO A SIMMETRIA CENTRALE
Appendice A
Probabilità di transizione in
regime di semi-classicità
In meccanica classica, come è noto, l’attraversamento di una barriera di potenziale
è un esempio di processo assolutamente impossibile; questo però, come abbiamo
visto, non accade in regime di semi-classicità, dove la probabilità del verificarsi di
tale evento è esponenzialmente piccola. L’obiettivo che ci poniamo adesso è quindi
quello di determinare l’esponente corrispondente alla probabilità che tale evento si
verifichi.
Consideriamo una transizione di un qualche sistema, da uno stato 1 ad uno stato
2 ; risolvendo le corrispondenti equazioni classiche del moto troviamo la traiettoria
della transizione, che risulterà però complessa, in accordo con l’impossibilità del
processo in meccanica classica. In particolare risulterà complesso il punto in cui
ha luogo la transizione del sistema da uno stato all’altro, chiamato proprio punto
di transizione ed indicato con q0 , e la cui posizione spaziale sarà determinata dalle
leggi di conservazione per la meccanica classica.
Dovremo adesso calcolare l’azione S1 (q1 , q0 )+S2 (q0 , q2 ) per il moto del sistema nel
primo stato, dalla posizione iniziale q1 al punto di transizione q0 , e successivamente
nel secondo stato, da q0 alla posizione finale q2 . La probabilità cercata sarà quindi
data dalla formula
2i
ω ∼ exp − [S1 (q1 , q0 ) + S1 (q0 , q2 )]
~
35
(A.1)
36APPENDICE A. PROBABILITÀ DI TRANSIZIONE IN REGIME DI SEMI-CLASSICITÀ
se la posizione del punto di transizione q0 non è univoca, si dovrà scegliere tra tutte
quella per cui l’esponente della (A.1) abbia valore assoluto minimo, valore che dovrà
comunque essere sufficientemente grande per garantire l’applicabilità della formula.
Il metodo delle traiettorie complesse classiche basato sull’equazione (A.1) ha carattere generale, ed è applicabile alle transizioni in sistemi con un numero arbitrario
di gradi di libertà. Se il punto di transizione è reale, ma si trova in una regione classicamente inaccessibile, la nostra formula coincide con l’espressione (2.1), relativa
alla probabilità che si verifichi l’effetto tunnel.
A.1
Riflessione al di sopra di una barriera di
potenziale
Applichiamo ora l’equazione (A.1) al problema della riflessione in presenza di una
barriera di potenziale, con E > V (x). In questo caso il nostro punto di transizione
q0 non è altro che il punto d’inversione del moto, indicato dalla coordinata complessa
x0 , il cui valore è dato dalla radice dell’equazione
q
V (x) − E. Il nostro obiettivo
sarà quello di dimostrare come in questo caso sarà possibile calcolare il coefficiente
di riflessione e contemporaneamente il coefficiente che precede l’esponenziale.
Dobbiamo innanzitutto stabilire una corrispondenza tra la funzione d’onda a destra della nostra barriera, cioè quella trasmessa, e quella a sinistra della barriera, che
sarà data dall’interazione dell’onda incidente con quella riflessa. Scriviamo l’onda
trasmessa come
ψ+ = q
1
e
i
~
x
x1
p(x0 )dx0
p(x)
e seguiamo la sua variazione lungo il cammino C nel semipiano superiore che gira
intorno al punto d’inversione x0 . L’ultimo tratto di questo cammino dovrà necessariamente trovarsi a sinistra e sufficientemente lontano dal punto d’inversione,
in modo tale da rendere l’errore della funzione, approssimata mediante il metodo
WKB, minore rispetto alla grandezza ψ− cercata. L’aggiramento del punto x0 implica il cambiamento di segno nella radice che ne determina in valore, che diventerà
q
E − V (x); questo farà tornare la nostra funzione ψ+ sull’asse reale, trasformandosi
A.1. RIFLESSIONE AL DI SOPRA DI UNA BARRIERA DI POTENZIALE 37
Figura A.1:
nella funzione ψ− , che si propaga verso sinistra, che non è altro che l’onda riflessa
cercata.
Le ampiezze delle onde incidenti e riflesse si possono considerare come coincidenti,
quindi il coefficiente di riflessione R sarà dato semplicemente da
2i
ψ−
R = | |2 = exp −
ψ+
~
!
p(x)dx
C
Dopo aver ottenuto questa formula si può deformare arbitrariamente il cammino d’integrazione dell’esponenziale. Trasformandolo per esempio nel cammino C 0
rappresentato in figura (A.1), l’integrale si riduce al doppio dell’integrale lungo il
cammino da x1 ad x0 , e otteniamo quindi
R=e
−4σ(x1 ,x0 )/~
x0
con σ = i
p(x)dx
(A.2)
x1
la scelta di x1 sarà inoltre arbitraria, poiché la funzione p(x) è reale su tutto l’asse
reale.
Come già detto, tra tutti i valori possibili di x0 dovremo scegliere quello che
minimizza il valore dell’esponenziale nell’equazione (A.2), inoltre dovrà essere sufficientemente maggiore di uno, poiché andranno considerati soltanto punti x0 per cui
σ > 0, appartenenti cioè al semipiano superiore. Inoltre, nel caso limite in cui E sia
tanto grande da rendere σ 1, sarà applicabile la teoria delle perturbazioni.
38APPENDICE A. PROBABILITÀ DI TRANSIZIONE IN REGIME DI SEMI-CLASSICITÀ
Bibliografia
[1] Ravanini Francesco, Dispense per il corso di Istituzioni di Fisica Teorica, pp.
72-95
[2] Jeffreys Harold (1924), "On certain approximate solutions of linear differential
equations of the second order", Proceedings of the London Mathematical Society
36, 428-436
[3] Wentzel Gregor (1926), "Eine Verallgemeinerung der Quantenbedingungen für
die Zwecke der Wellenmechanik", Zeitschrift für Physik 38, 518–529
[4] Kramers Hendrik Anthony (1926), "Wellenmechanik und halbzählige
Quantisierung", Zeitschrift für Physik 39, 828–840
[5] Brillouin Léon (1926), "La mécanique ondulatoire de Schrödinger: une méthode générale de resolution par approximations successives", Comptes Rendus de
l’Academie des Sciences 183, 24–26
[6] Landau Lev Davidovič e Lifšic Evgenij Mikhailovič (1978), Fisica Teorica
Vol. 3: Meccanica Quantistica. Teoria non relativistica, Riuniti, pp. 215-219,
231-236
[7] Griffiths David J. (1995), Introduction to Quantum Mechanics, Prentice Hall,
pp. 274-292
39