Indici vari - schedematematica

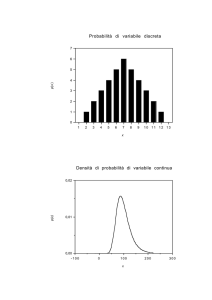
SCHEDE SULLE VARIABILI CASUALI
Nozione
Variabile casuale (o aleatoria): insieme ordinato di valori numerici (che rappresentano un insieme delle risposte), ciascuno
associato ad una probabilità; la somma delle probabilità dev’essere 1.
Le variabili casuali possono essere discrete, se i valori sono associabili a numeri naturali, o continue, se non lo sono (perché i
valori sono “troppi” per poter essere contati).
Nel seguito si tratterà soltanto di variabili casuali discrete, che possono essere rappresentate in modo simile a quello usato
per le distribuzioni di frequenza.
Esempio: qual è la variabile casuale per le risposte alla domanda: su 3 lanci di monete, qual è la probabilità che escano x
teste?
L’insieme delle risposte, associato alle rispettive probabilità, è in questa tabella.
x: numero di teste in 3 lanci di monete
p: probabilità
x1 = 0
p1 = 1/8
x2 = 1
p2 = 3/8
x3 = 2
p3 = 3/8
x4 = 3
p4 = 1/8
La variabile casuale è data da tutti i valori possibili come risposta alla domanda, cioè 0, 1, 2 e 3.
Le probabilità sono ottenute calcolandole per ogni valore e usando la probabilità classica.
Tre lanci di monete danno 8 possibili risultati: 2 per il primo lancio, 2 per il secondo e 2 per il terzo, che vanno moltiplicati.
Esiste un solo modo di avere 0 teste ed è che in tutti i tre lanci sia uscita croce.
Esistono 3 modi di avere 1 testa, a seconda che la testa sia uscita al primo, al secondo o al terzo lancio.
Esistono 3 modi per avere 2 teste, a seconda che la croce sia uscita al primo, al secondo o al terzo lancio.
Esiste un solo modo di avere 3 teste ed è che in tutti i tre lanci sia uscita testa.
La tabella rappresenta una variabile casuale x discreta.
Si noti che la somma delle probabilità dà 1.
Esempio: se lancio due dadi con 6 facce, qual è la probabilità che la somma dei due esiti sia x?
L’insieme delle risposte, associato alle rispettive probabilità, è in questa tabella.
x
p
2
1/36
3
2/36
4
3/36
5
4/36
6
5/36
7
6/36
8
5/36
9
4/36
10
3/36
11
2/36
12
1/36
La variabile casuale è data da tutti i valori possibili come risposta alla domanda, cioè gli interi da 2 = 1+1 a 12 = 6+6.
Le probabilità sono ottenute calcolandole per ogni valore e usando la probabilità classica.
I possibili risultati sono 36: sono 6 per il primo dado e, per ciascuno di questi risultati, 6 per il secondo dado.
Esiste un solo modo di avere come risultato 2, cioè 1+1.
Allo stesso modo, esiste un solo modo di aver come risultato 12, cioè 6+6.
Esistono due modi per avere come risultato 3, cioè 1+2 e 2+1.
Allo stesso modo, esistono due modi per aver come risultato 11, cioè 5+6 e 6+5.
Esistono tre modi per avere come risultato 4, cioè 1+3, 2+2 e 3+1.
Allo stesso modo, esistono tre modi per aver come risultato 10, cioè 4+6, 5+5 e 6+4.
Continuando così, si arriva a trovare tutte le probabilità.
Si noti che la somma delle probabilità dà 1.
Funzione di ripartizione
Funzione di ripartizione: insieme ordinato di valori numerici (che rappresentano un insieme delle risposte), ciascuno associato
alla somma delle probabilità dei valori minori o uguali ad esso.
Esempio: si vuole ottenere la funzione di ripartizione della seguente variabile casuale, calcolata sopra.
x: numero di teste in 3 lanci di monete
p: probabilità
0
1/8
1
3/8
2
3/8
3
1/8
La funzione di ripartizione è questa.
1
x: numero di teste in 3 lanci di monete
F(x): funzione di ripartizione
0
1/8
1
4/8 = 0,5
2
7/8
3
8/8 = 1
La funzione di ripartizione serve quindi a conoscere la probabilità che la variabile assuma valori minori o uguali ad un certo
valore di x.
Valgono perciò le seguenti relazioni.
p(xa) = F(a).
p(x<a) = F(a)p(a).
p(x>a) = 1F(a).
p(xa) = 1F(a)+p(a).
p(a<xb) = F(b)F(a).
È possible trovare altre varianti sul tema, come p(a<x<b), che si lasciano per esercizio.
Indici vari
Come per le distribuzioni di frequenza, anche per le variabili casuali si può calcolare moda, mediana, varie medie e scarto
quadratico medio.
In genere, la media artitmetica, trattando di variabili casuali, viene chiamata valore atteso o speranza matematica. Si calcola
usando le probabilità invece delle frequenze e, dato che il totale delle probabilità è 1, non serve dividere per esso.
Ecco un tipico uso del valore atteso: mi trovo davanti a due possibili eventi: il primo può capitare con una probabilità di 0,3
e dà un guadagno di 120 euro; il secondo può capitare con una probabilità di 0,7 e dà un guadagno di 100 euro. Qual è il
guadagno medio M? Cioè, che guadagno mi aspetto?
Il ragionamento si può svolgere così: una probabilità frequentistica di 0,3 significa che in media, su 10 situazioni, in 3 capita
l’evento; similmente per 0,7. Perciò, se considero 10 situazioni, il guadagno totale è 10M.
Il primo evento capita in media 3 volte, perciò il guadagno quando capita il primo evento è 3120; similmente, quando
capita il secondo evento il guadagno è 7100. Il guadagno totale perciò è 3120+7100.
Confrontando i due diversi modi di scrivere il guadagno totale, si ha 10M = 3120+7100.
Isolando M, si ha M = (3120+7100)/10.
L’ultima uguaglianza si può scrivere anche come M = (3/10)120+(7/10)100.
In termini di probabilità frequentistica, si arriva a M = 0,3120+0,7100 (che, per la cronaca, fa 106).
Usiamo i simboli invece dei numeri; si ha che, avendo un evento con probabilità p1 e guadagno x1 e un altro evento con
probabilità p2 e guadagno x2 , bisogna trovare il guadagno medio (atteso) M.
Le probabilità, se trattate in senso frequentistico, possono essere scritte come p1 = f1/(f1+f2) e p2 = f2/(f1+f2).
Quindi ci sono f1+f2 casi totali, f1 in cui capita il primo evento e f2 in cui capita il secondo evento.
Il guadagno medio potrà essere trovato partendo da (f1+f2)M = f1x1+f2x2 , che dà M 
f1
f2
x1 
x2 .
f1  f 2
f1  f 2
Tornando infine alle probabilità, si ottiene
M = p1x1+p2x2 .
Naturalmente, gli stessi ragionamenti valgono anche con più di due eventi.
Può essere utile introdurre un nome per i prodotti p1x1 , p2x2 , p3x3 , ..., pnxn . Chiamiamoli valori attesi parziali, dato che la loro
somma è appunto il valore atteso (totale).
Esempio: si calcoli il valore atteso e lo scarto quadratico medio (con la formula ridotta) per la seguente variabile casuale, già
usata sopra.
x: numero di teste in 3 lanci di monete
p: probabilità
0
1/8
1
3/8
2
3/8
3
1/8
Si ottiene questa tabella.
x
0
p
0,125
xp
0
x2p
0
2
1
0,375
2
0,375
3
0,125
somme = medie
0,375
0,75
0,375
1,5
0,375
1,5
1,125
3
Il valore atteso risulta M = 1,5; la varianza è VAR = 31,52 = 0,75; lo scarto quadratico medio è SQM = 0,75 = 0,866.
Giochi equi
Un gioco d’azzardo è equo se il valore atteso (totale) di ogni giocatore è nullo.
Esempio: dato che, per il decreto 179 del ministero dell’economia e delle finanze del 19 giugno 2003, art. 5, la posta dei
concorsi a pronostici va al montepremi soltanto per il 34,65%, il totocalcio non è un gioco equo.
Infatti i giocatori, nel loro complesso, puntano una somma s e vincono una somma V = 0,3465s. Il valore atteso sarebbe
perciò M = 0,3465pss = s(0,3465p1), che è sempre negativo, perché p può al massimo valere 1.
La distribuzione geometrica
Le variabili casuali con un valido significato scientifico sono molte, ma nel seguito si tratterà soltanto di due.
La variabile casuale geometrica risponde alla domanda: faccio parecchi tentativi, i cui esiti sono fra loro indipendenti; per
ciascuno dei tentativi ho una probabilità costante p di successo. Qual è la probabilità che il primo successo capiti al tentativo
numero k?
Se il primo successo è il numero k, allora tutti gli k1 precedenti tentativi sono fallimenti.
Se la probabilità di un successo è p, allora quella di un fallimento è 1p.
Gli eventi, cioè i primi k1 fallimenti e l’ultimo successo, devono capitare tutti, perciò vanno congiunti.
Gli esiti dei tentativi sono indipendenti, quindi, dato che vanno congiunti, le probabilità si possono moltiplicare.
Mettendo tutti questi ragionamenti insieme, si trova che per la variabile casuale geometrica G(k) vale la seguente regola di
calcolo.
G(k) = (1p)k1p.
Esempio: per un dato incontro, la probabilità che un venditore riesca a piazzare un prodotto è p = 0,2. Qual è la probabilità
che il venditore piazzi il suo primo prodotto al quarto incontro?
Il venditore deve aver avuto un fallimento per 3 incontri e un successo al quarto, perciò è G(4) = (10,2)30,2 = 0,1024.
Sicuramente G(k) rappresenta una probabilità; ma la successione delle G(k) serve a costruire una variabile casuale? La
risposta è affermativa, grazie al seguente teorema.
Teorema: è G(k) = 1.
Dimostrazione.
Rappresentiamo le formule in tabella.
k
G(k)
1
(1p)11p
=p
2
(1p)p
3
(1p)2p
...
...

(1p)1p = 0
Pertanto, bisogna calcolare la somma G(k) = p+(1p)p+(1p)2p+(1p)3p+...
Raccogliendo a fattor comune p e scrivendo per semplicità q invece di 1p, si ottiene G(k) = p(1+q+q2+q3+...).
In terza si è trovato il valore di 1+q+q2+q3+... per 1 < q < 1 (che è il nostro caso, perché q è una probabilità), cioè 1/(1q).
(Chi volesse avere sottomano la dimostrazione, può guardare le SCHEDE DI MATEMATICA FINANZIARIA 2, al
capitolo Le progressioni geometriche.)
Si arriva dunque a G(k) = p/(1q).
Dato che è stato posto sopra p = 1q, è anche q = 1p.
Perciò è G(k) = 1.
CVD
Teorema: il valore atteso di una variabile casuale geometrica con probabilità p è 1/p.
Dimostrazione.
Si riprende la tabella sopra.
3
k
G(k)
1
(1p)11p
=p
2
(1p)p
3
(1p)2p
...
...

(1p)1p = 0
Tuttavia qui bisogna mostrare, ricordando che le probabilità qui si chiamano G(k), che è M = kG(k) = 1/p.
Si cominci allora a scrivere kG(k) = 1p+2(1p)p+3(1p)2p+... .
Raccogliendo a fattor comune p e scrivendo per semplicità q invece di 1p, si arriva a kG(k) = p(1+2q+3q2+...).
C’è un legame fra il generico addendo kqk1 e qk, che è l’addendo generico della serie q+q2+q3+...: quello è la derivata di
questo rispetto a q.
La serie A = q+q2+q3+... è simile alla serie B = 1+q+q2+q3+...; l’unica differenza è il primo addendo. Perciò è A = B1.
Perciò è A = 1/(1q)1 = q/(1q).
Per trovare una buona formula per 1+2q+3q2+..., bisogna allora derivare A rispetto a q, ottenendo A’ = 1/(1q)2.
Si arriva dunque a kG(k) = p/(1q)2.
Dato che è stato posto sopra p = 1q, è anche q = 1p.
Perciò, semplificando, risulta M = kG(k) = 1/p.
CVD
Con accorgimenti simili, ma qualche complicazione in più, si dimostra che la variabile casuale geometrica ha SQM =
(1p)0,5p.
Esempio: trovare il valore atteso e lo scarto quadratico medio per l’esempio precedente.
Il venditore avrà il primo successo in media al tentativo numero 1/0,2 = 5, con uno scarto quadratico medio pari a
(10,2)0,50,2 = 0,1789.
La distribuzione binomiale
La variabile casuale binomiale risponde alla domanda: faccio parecchi tentativi, i cui esiti sono fra loro indipendenti; per
ciascuno dei tentativi ho una probabilità costante p di successo. Qual è la probabilità di ottenere k successi su un totale di n
tentativi?
La geometrica quindi è un caso particolare della binomiale: è come se nella binomiale fosse k = 1 e inoltre quest’unico
successo dovesse capitare soltanto in una posizione ben precisa della successione (all’ultimo posto).
Se la probabilità di un successo è p, allora quella di un fallimento è 1p.
Gli eventi, cioè i successi e i fallimenti, devono capitare tutti, perciò vanno congiunti.
Gli esiti dei tentativi sono indipendenti, quindi, dato che vanno congiunti, le probabilità si possono moltiplicare.
Se tutti i successi capitassero all’inizio della successione e tutti i fallimenti alla fine, la probabilità sarebbe pk(1p)nk.
Ma i successi possono benissimo essere sparpagliati sugli n tentativi, quindi ci sono molti più casi.
Per sapere quanti casi ci sono, serve il calcolo combinatorio: il mio insieme di origine è quello degli n tentativi; i miei insiemi
destinazione sono quelli dei k successi. Non mi sto chiedendo quale successo è capitato per primo o per secondo o così via,
perciò negli insiemi destinazione non conta l’ordine; non ha senso immaginare che un successo con un dato tentativo si
ripeta (ogni tentativo esaurisce la possibilità di avere un dato successo), perciò negli insiemi destinazione non c’è ripetizione.
Abbiamo perciò a che fare con combinazioni senza ripetizione, il cui numero è
n
  .
k 
Mettendo tutti questi ragionamenti insieme, si trova che per la variabile casuale binomiale B(k) vale la seguente regola di
calcolo.
n
nk
Bk     p k 1  p  .
k 
Esempio: la probabilità che una ciliegia abbia un verme è 0,003. In un cestino di 40 ciliegie, qual è la probabilità di non
trovare vermi? E di trovarne almeno 1?
La probabilità di non trovare vermi è k = 0, con p = 0,003 e n = 40.
La formula dà
 40 
40  0
B0   0,0030 1  0,003
 0,997 40  0,88676 .
0
 
Trovare almeno un verme è negare di non trovare alcun verme, perciò la probabilità trovare almeno un verme è data da B(1,
2, ..., 40) = 10,88676 = 0,11324.
4
Sicuramente B(k) rappresenta una probabilità; ma la successione delle B(k) serve a costruire una variabile casuale? La
risposta è affermativa, grazie al seguente teorema.
Teorema: è B(k) = 1.
Dimostrazione.
n
  rappresenta i termini del triangolo di Tartaglia (chi non conoscesse la dimostrazione, può trovarla su
k 
n k
nk
http://it.wikipedia.org/wiki/Triangolo_di_Tartaglia), quindi Bk     p 1  p 
rappresenta lo sviluppo della
k 
n k
nk
n
potenza di un binomio. Perciò è   p 1  p 
  p  1  p   1n  1 .
k 
Il coefficiente
CVD
Ecco, senza dimostrazione, le formule per il valore atteso e lo scarto quadratico medio.
M = np;
SQM = [np(1p)].
Esempio: trovare il valore atteso e lo scarto quadratico medio per l’esempio precedente.
In un cestino in media ci sono 0,00340 = 0,12 vermi, con uno scarto quadratico medio di 0,34589.
5