1
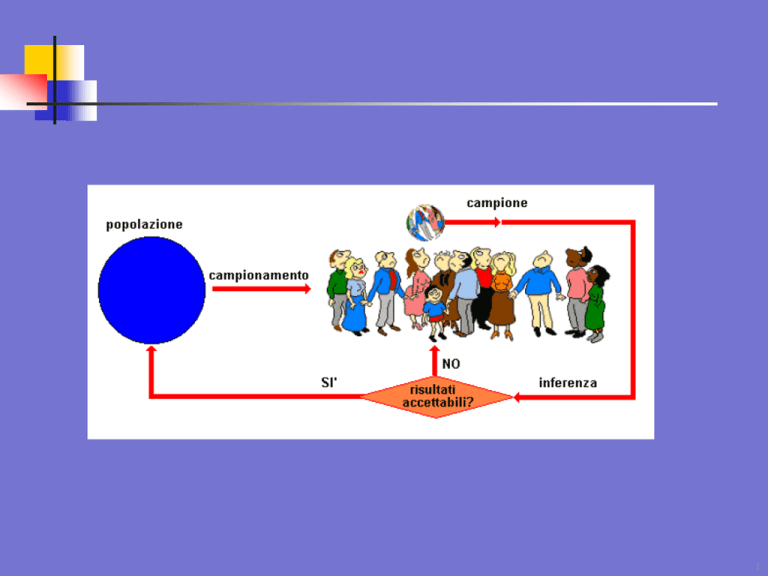
Inferenza Statistica
Le componenti teoriche dell’Inferenza Statistica sono:
la teoria dei campioni
la teoria della probabilità
la teoria della stima dei parametri
la teoria della verifica delle ipotesi
2
Probabilità
Il concetto di probabilità è espresso di frequente
nella pratica quotidiana: un cliente ha la probabilità
di stare bene in un albergo a 5 stelle 95 volte su
100, una compagnia aerea 9 volte su 10 è
puntuale… etc.
Incertezza e Probabilità
Devono rientrare delle navi, come sarà il tempo?
•
•
•
•
esperienza relativa alle
condizioni del tempo dei
giorni precedenti
tempo previsto nella
stagione considerata
previsioni meteo
saranno fatte valutazioni
probabilistiche per
minimizzare possibili errori
di previsione
Probabilità: l’accadere di un certo evento è più o
meno verosimile in relazione ad altri eventi
4
Incertezza e Probabilità
Prova: esperimento in cui si riscontra incertezza nel risultato
Evento aleatorio: uno dei possibili risultati di una prova
la realizzazione delle prove darà poi luogo ad uno e ad un solo
risultato tra i possibili previsti (modalità disgiunte)
es. lancio di una moneta, dado, etc...
al momento in cui l’esperimento è compiuto,
il risultato possa essere noto, oppure no al ricercatore
Evento certo: si verifica sicuramente
Evento impossibile: non può mai realizzarsi
5
Impostazione Assiomatica (Kolmogorov)
1) POSITIVITA’ :
P(E)≥0
2) CERTEZZA:
P(E)=1
se E vento certo
3) UNIONE:
se A e B sono due eventi incompatibili (mutuamente esclusivi)
P(AUB)= P(A)+ P(B)
6
In conclusione:
0 ≤ P(A) ≤ 1
la probabilità del verificarsi di due o più eventi incompatibili è pari
alla somma delle singole probabilità
7
APPROCCIO FREQUENTISTA
Si consideri il lancio di un dado di caratteristiche ignote e si calcoli la
probabilità che si verifichi l’evento (un qualsiasi possibile risultato del lancio):
“uscita di una faccia contraddistinta da un numero pari”
dall’osservazione del fenomeno risulta che:
al ripetersi dei lanci, le facce contraddistinte da numeri pari escono circa la
metà delle volte rispetto alle facce dispari e che sempre più, al progressivo
ripetersi del numero dei lanci, nell’uscire, tendono a stabilizzarsi sulla metà
delle volte
allora si può affermare che:
al ripetersi dei lanci “sempre sotto le medesime condizioni”,
la probabilità (compresa tra 0 e 1) che esca una faccia contraddistinta da un
numero pari sarà 0,50
8
Scuola frequentista
L’evento E è un possibile risultato di un esperimento ripetibile
n = numero di prove effettuate
m = numero di eventi che si sono verificati
F= frequenza assoluta
Fn ( E )
P( E ) lim
n
n
Al tendere del tempo all’infinito, m/n si stabilizza, esprimendo la
probabilità di verificarsi dell’evento
9
Variabile casuale
VARIABILE CASUALE X: qualsiasi caratteristica si presenti con modalità diverse x1,
x2, x3,…, da soggetto a soggetto o, nello stesso soggetto, da un momento all’altro
Modalità: tutti i valori che la variabile può assumere
Variabile casuale: quantitativa (continua, discreta)
qualitativa (nominale, ordinale)
prima di una data prova, può assumere in ciascuna osservazione un valore qualsiasi,
dopo la prova, essa assumerà, in ciascuna osservazione, uno ed un solo valore, detto
“determinazione della variabile casuale”
VARIABILE DETERMINISTICA: variabile casuale dopo una determinata prova.
10
Distribuzione di probabilità
I valori possibili (modalità) di una variabile casuale sono
riassunti in una distribuzione, definita “distribuzione di
probabilità”
Nella distribuzione di probabilità sono mostrati tutti i
possibili valori di una variabile casuale con le rispettive
probabilità di verificarsi
11
Distribuzioni di frequenza e distribuzioni
di probabilità
Una distribuzione di
frequenza mostra il risultato
di ogni evento e la sua relativa
frequenza
Una distribuzione di
probabilità elenca ogni
valore possibile con la relativa
probabilità
12
Alcune distribuzioni di probabilità
Variabili discrete
Binomiale
Poisson
Variabili continue
Normale
Normale Standardizzata
t di Student
13
Distribuzione Binomiale
Variabile casuale discreta dicotomica
assume
1= successo con probabilità p
0= insuccesso con probabilità q=1-p
uno ed un solo risultato tra i due possibili;
la probabilità è la stessa per ogni prova
tutte le prove sono indipendenti
Funzione di probabilità:
14
Distribuzioni di Poisson
p = probabilità che l’evento si verifichi
n = numero delle prove
p < 0,05
n > 100
Funzione di probabilità
Dove λ è il numero medio di eventi per intervallo di tempo
15
Distribuzione Normale
Variabile casuale continua
Molti dei dati rilevati tendono a
distribuirsi secondo le caratteristiche della
normalità
Più numerose saranno le osservazioni
sulla variabile, più numerosi saranno i
rettangoli componenti l’istogramma più
il grafico si approssimerà ad una curva a
campana
16
Distribuzione Normale e Normale standardizzata
Funzione di densità
1
f (x) =
×e
s 2P
(x- m )2
2s
2
- ¥ < x < +¥
17
Probelma:
Distribuzioni Probabilità del verificarsi di un evento
L’evento segue una distribuzione di probabilità
Come si calcola la probabilità?
La velocità di consegna da parte di un’azienda con sede
a Barcellona, segue una distribuzione normale ed ha una
media di 185,7 giorni ed una deviazione standard di 14,6
giorni. Qual’è la probabilità che se faccio un ordine
questo sia in sede dopo 200 giorni?
18
Esempio - Punteggi Standardizzati
La velocità di consegna ha una media di 185,7 giorni ed una deviazione
standard di 14,6 giorni
zi
xi
Valori critici
densità
Distribuzione Normale Standardizzata
19
Esempio - Punteggi Standardizzati
Ad un test, la media della durata di una batteria è 72 ore e la
deviazione standard è 15 ore. Qual è la probabilità che acquistando
una batteria, questa si scarichi dopo 60 ore ma prima di 90?
zi
xi
;
60 72
93 72
z60
0,8; z93
1,4
15
15
Valori critici
20
Distribuzione t
la distribuzione t di Student è una distribuzione simmetrica,
con media 0 e con deviazione standard, caratterizzata dai
gradi di libertà.
Al variare della numerosità campionaria, varia il numero dei
gradi di libertà e, conseguentemente, varia la forma della
distribuzione
21
Gradi di libertà
1920: Fisher introduce i gradi di libertà
Esprimono il numero minimo di dati sufficienti a valutare
la quantità d'informazione contenuta. Quando un dato
non è indipendente, l'informazione che esso fornisce è già
contenuta implicitamente negli altri. È possibile quindi
calcolare le statistiche utilizzando soltanto il numero di
osservazioni indipendenti, consentendo in questo modo di
ottenere una maggiore precisione nei risultati.
22
1,96 SD
95 %
2,262 SD
95 %
23
Confronto tra la distribuzione t di Student e la curva
Normale Standardizzata
24
25












