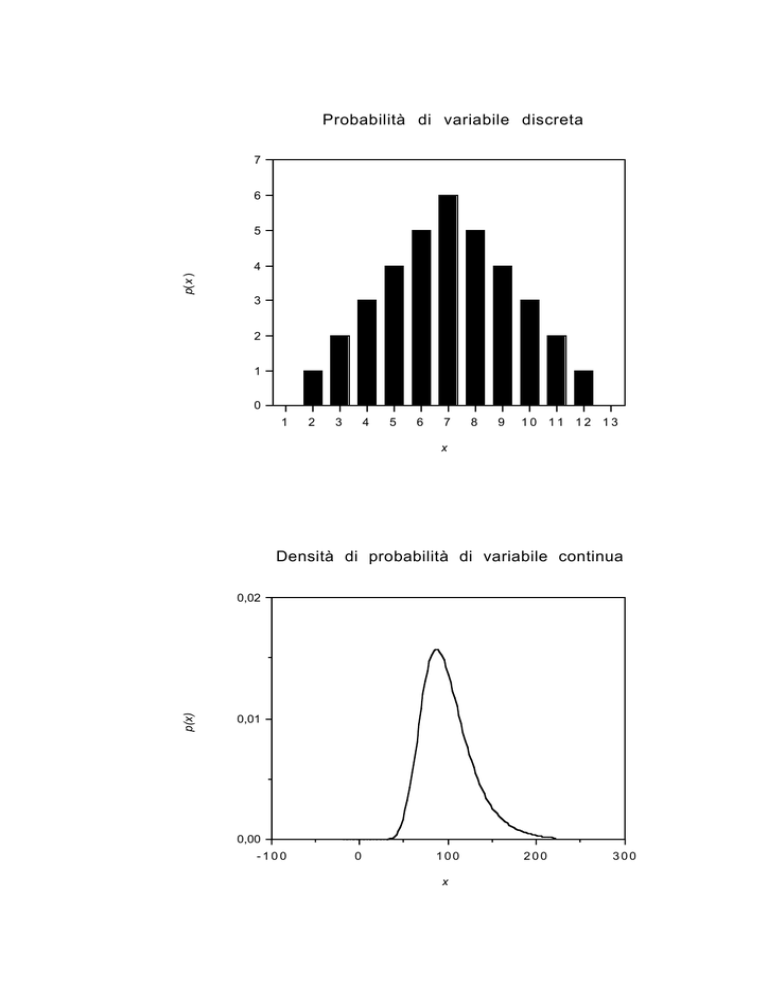
Probabilità di variabile discreta
7
6
5
p(x )
4
3
2
1
0
1
2
3
4
5
6
7
8
9
10 11 12 13
x
Densità di probabilità di variabile continua
p(x)
0,02
0,01
0,00
-100
0
100
x
200
300
Variabile discreta
Momento: di r-esimo ordine rispetto al valore x 0:
µr' ( x ) =
N
∑ (x i
i= 1
- x 0 ) r p ( x i)
Momento di primo ordine rispetto all'origine (media
aritmetica):
µ (x ) =
N
∑x ip(x i)
i= 1
Momento di r-esimo ordine rispetto alla media:
µ r( x ) =
N
∑ [x i
i= 1
- µ ( x ) ] r p ( x i)
Momento del secondo ordine rispetto alla media
(varianza):
σ 2(x )
=
N
∑ [x i
i= 1
- µ ( x )] 2 p ( x i )
Variabile continua
Momento di r-esimo ordine rispetto al valore x 0:
µr' ( x ) =
+∞
∫
-∞
(x - x 0 ) r p (x )d x
Momento di primo ordine rispetto all'origine (media
aritmetica):
µ (x ) =
+∞
∫xp(x)d x
-∞
Momento di r-esimo ordine rispetto alla media:
µ r( x ) =
+∞
∫ [x
-∞
- µ ( x )] r p ( x ) d x
Momento del secondo ordine rispetto alla media
(varianza):
σ 2(x )
+∞
=
[x
∫
-∞
- µ (x )] 2 p (x )d x
Misure di tendenza centrale
Media aritmetica
E` il momento del primo ordine rispetto
all'origine.
Mediana
Si definisce mediana della distribuzione della
¨
¨
variabile x il valore x la cui probabilità P(x ) è
uguale a 0,50.
Moda
Si definisce m o d a della distribuzione di una
~
variabile casuale x il valore x
a cui
corrisponde un massimo della funzione p(x).
Una distribuzione con più mode si dice
multimodale.
Misure di dispersione
Misura di dispersione omogenea con la
media: scarto quadratico medio
Si definisce scarto quadratico medio della
variabile casuale x la radice quadrata σ (x) della
sua varianza.
Misura di dispersione
coefficiente di variazione
adimensionale:
Si chiama coefficiente di variazione il rapporto
tra lo scarto quadratico medio e la media della
variabile casuale x
C V (x ) =
σ (x )
µ (x)
Misura
di
asimmetria
coefficiente di asimmetria
adimensionale:
Con il termine coefficiente di asimmetria
(skewness) si indica il rapporto tra il momento
del terzo ordine e il cubo dello scarto
quadratico medio della distribuzione
µ 3 (x )
γ (x ) = 3
σ (x)
Probabilità di variabile funzione non
decrescente di una variabile casuale
y = φ (x )
y a = φ (x a )
x ≤ xa → y ≤ ya
P(x a ) = P(y a )
P (x) = P (y)
e differenziando:
p (y ) = p (x )
dx
dy
Caso particolare: y funzione lineare crescente di x
y = ax + b
µ ( y) = a µ (x) + b
σ (y) = a σ (x)
x
0
50
100
150
1
3
5
7
9
m =1
11
13
xa
15
m=7
17
19
21
23
m = 11
t
25
27
29
m=4
31
33
35
m=3
37
39
m=6
41
43
45
47
49
m=8
Tempo di ritorno
p (m ) = P (x a ) m - 1 [1 - P (x a ) ]
µ (m ) =
∞
∑ m p (m )
m=1
=
∞
∑ m P (x a ) m -1 [1 - P (x a ) ]
m=1
∞
∑ m z m -1 = ( 1 -1z ) 2
m=1
µ (m ) =
1
1 - P (x a )
T (x ) =
1
1 - P (x)
Il tempo di ritorno risulta misurato in numero di
osservazioni.
Distribuzione binomiale
Probabilità dell'evento uguale a θ
N numero delle osservazioni
m numero delle osservazioni in cui l'evento si
verifica
m è una variabile casuale discreta
m può assumere tutti i valori dell'intervallo (0, N)
(estremi compresi)
p(m) probabilità del valore m
Distribuzione binomiale:
probabilità p(m) del valore m
Esempio con N = 5 ed m = 2:
1
2
3
4
5
Probabilità della combinazione di osservazioni:
(1 - θ ) θ (1 - θ ) θ (1 - θ )
Probabilità di una particolare combinazione in cui
l'evento si verifica m volte su N:
θ m (1 - θ ) N - m
Numero delle combinazioni:
N
m
Probabilità del valore m:
p (m ) =
N
θ m (1
m
- θ )N - m
Distribuzione binomiale
θ = 0,3
N =10
0,3
p(m)
0,2
0,1
0,0
0
1
2
3
4
5
6
7
8
9
10
m
(per m uguale a 9 e per m uguale a 10 la
probabilità è molto vicina a zero)
Distribuzione binomiale
θ = 0,6
N =10
0,3
p(m)
0,2
0,1
0,0
0
1
2
3
4
5
6
7
8
9
10
m
(per m uguale a 0 la probabilità è molto vicina a
zero)
Distribuzione binomiale
Parametri:
µ (m ) = N θ
N θ (1 - θ )
σ (m ) = √
Distribuzione di Poisson
E` una forma limite della distribuzione binomiale.
Ipotesi:
N θ = λ = costante
N→∞
θ→ 0
Probabilità:
λm
p(m ) = exp(- λ )
m!












