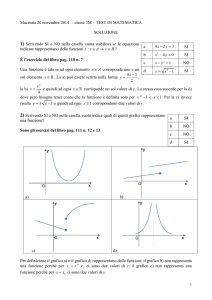
M. Barlotti
“Esercizi di Algebra”
v. !."
Capitolo 1 Pag. 1
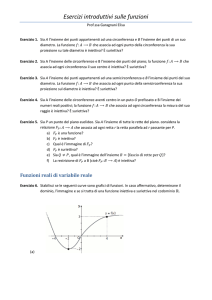
1. Esercizi su: iniettività e suriettività delle funzioni.
Esercizio 1.1
Sia c l’insieme dei numeri primi, e sia Y l’insieme dei sottoinsiemi finiti di c (dunque:
X − Y se e soltanto se X è un insieme finito di numeri primi).
Sia 0 : ÏÖ!, "× Ä Y la funzione che ad ogni numero naturale non inferiore a # associa
l’insieme dei suoi fattori primi (dunque, ad esempio: 0 ('!) œ Ö#, $, &×, 0 (" ")$) œ Ö(, "$× ).
Si dica, motivando la risposta, se 0 è iniettiva e/o suriettiva.
Esercizio 1.2
Sia k ³ Ö", #, $, %, &×. Si dica, motivando la risposta, quali delle seguenti sono funzioni
k Ä k , precisando per ciascuna di esse (in caso affermativo) se è iniettiva e/o suriettiva:
( 3)
0 definita dalle condizioni:
0 (%) ³ %, 0 (#) ³ $, 0 (") ³ %, 0 (#) ³ ", 0 ($) ³ #, 0 (%) ³ &, 0 (&) ³ " ;
(33)
1 definita dalle condizioni: 1($) ³ ", 1(%) ³ #, 1(") ³ %, 1(&) ³ $, 1(#) ³ " ;
(333)
2 definita dalle condizioni: 2(#) ³ ", 2($) ³ %, 2(") ³ &, 2(%) ³ #, 2(&) ³ $ .
(3@)
3 definita dalle condizioni: 3(#) ³ $, 3($) ³ ", 3(%) ³ &, 3(#) ³ $, 3(&) ³ # .
Esercizio 1.3
È data la funzione f : p così definita:
#
Ú
Ý 8
#
f(8) ³ Û
Ý
Ü $8 #
se 8 è pari
se 8 è dispari
Si dica, motivando la risposta, se f è iniettiva, se f è suriettiva, se f è biiettiva.
Esercizio 1.4
È data la funzione f : {$, &, (, *, "!} Ä {$, &, ), "!} così definita:
f($) ³ ),
f(&) ³ "!,
f(() ³ ),
f(*) ³ &,
f("!) ³ $ .
Si dica, motivando la risposta, se f è iniettiva, suriettiva e/o biiettiva.
M. Barlotti
“Esercizi di Algebra”
v. !."
Capitolo 1 Pag. 2
Esercizio 1.5
È data la funzione f : p così definita:
#
Ú
Ý 8
%
f ( 8) ³ Û
Ý
Ü $8 1
se 8 è pari
se 8 è dispari
Si dica, motivando la risposta, se f è iniettiva, se f è suriettiva, se f è biiettiva.
Esercizio 1.6
Sia k ³ Ö", #, $, %, &×. Si dica, motivando la risposta, quali delle seguenti sono funzioni
k Ä k , precisando per ciascuna di esse (in caso affermativo) se è iniettiva e/o suriettiva:
( 3)
0 definita dalle condizioni: 0 (%) ³ &, 0 ($) ³ %, 0 (") ³ #, 0 (#) ³ $, 0 (&) ³ # ;
(33)
1 definita dalle condizioni: 1(") ³ %, 1(#) ³ #, 1($) ³ ", 1(#) ³ #, 1(&) ³ $ ;
(333)
2 definita dalle condizioni: 2(3) ³ ", 2(4) ³ %, 2(2) ³ &, 2(5) ³ #, 2(1) ³ $ ;
(3@)
3 definita dalle condizioni:
3(%) ³ ", 3(#) ³ %, 3(") ³ &, 3(#) ³ $, 3($) ³ &, 3(%) ³ ", 3(&) ³ # .
Esercizio 1.7
È data la funzione f : {$, &, (, *, "!} Ä {$, &, ), "!} così definita:
f($) ³ "!,
f(&) ³ ),
f(() ³ &,
f(*) ³ ),
f("!) ³ $ .
Si dica, motivando la risposta, se f è iniettiva, suriettiva e/o biiettiva.
Esercizio 1.8
È data la funzione f : p così definita:
#
Ú
Ý 8
#
f(8) ³ Û
Ý
Ü $8 #
se 8 è pari
se 8 è dispari
Si dica, motivando la risposta, se f è iniettiva, se f è suriettiva, se f è biiettiva.
M. Barlotti
“Esercizi di Algebra”
v. !."
Capitolo 1 Pag. 3
Esercizio 1.9
È data la funzione f : {#, %, ', ), *} Ä {#, %, (, *} così definita:
f(#) ³ (,
f(%) ³ *,
f(') ³ (,
f()) ³ %,
f(*) ³ # .
Si dica, motivando la risposta, se f è iniettiva, suriettiva e/o biiettiva.
Esercizio 1.10
È data la funzione f : p così definita:
#
Ú
Ý 8
#
f(8) ³ Û
Ý
Ü $8
se 8 è pari
se 8 è dispari
Si dica, motivando la risposta, se f è iniettiva, se f è suriettiva, se f è biiettiva.
Esercizio 1.11
È data la funzione f : {#, %, ', ), *} Ä {#, %, (, *} così definita:
f(#) ³ *,
f(%) ³ (,
f(') ³ %,
f()) ³ (,
f(*) ³ # .
Si dica, motivando la risposta, se f è iniettiva, suriettiva e/o biiettiva.
Esercizio 1.12
È data la funzione f : p così definita:
#
Ú
Ý 8
%
f ( 8) ³ Û
Ý
Ü $8 #
se 8 è pari
se 8 è dispari
Si dica, motivando la risposta, se f è iniettiva, se f è suriettiva, se f è biiettiva.