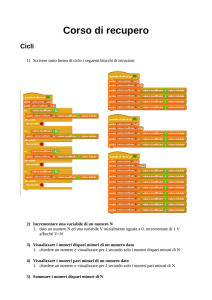
Istituzioni di Matematiche I a.a. 2000-2001
25 settembre 2001
1.
Si scriva 24710 in base 11, si calcoli 426×256 in base 6 e si trovi, se esiste, una base x per cui
valga l’uguaglianza
341x + 513x = 1154x.
2. Sia A l’insieme dei numeri multipli di 4 compresi fra 19 e 39 e sia B l’insieme dei numeri pari
compresi fra 7 e 17. Si diano un esempio di corrispondenza iniettiva da A a B, un esempio di
corrispondenza suriettiva da A e B e si dica se esiste una corrispondenza biunivoca fra A e B.
3. Si determini il MCD fra 54.126 e 30.246.
4. Si dimostri che il prodotto di due multipli di 15 è divisibile per 25.
5. Si dica se le seguenti affermazioni sono vere o false e si fornisca giustificazione delle risposte
date: il prodotto di due numeri pari è un numero pari; la somma di due numeri dispari è un
numero dispari; il prodotto di un numero pari e di un numero dispari è un multiplo di 6.
6.
Nell’insieme N dei numeri naturali si consideri la relazione R così definita: aRb se la somma
a+b è dispari. Si mostri, giustificando la risposta, che la relazione R è simmetrica e si
determinino gli elementi che sono in relazione con a=5 e quelli che sono in relazione con a=7.
Si dica, giustificando la risposta, se la relazione R è di equivalenza.
7. Si dimostri che l’affermazione: “Ogni numero naturale è dispari oppure è divisibile per 4” è
falsa. Si scriva la sua negazione.
8. Tre numeri naturali A, B e C hanno per somma 180. Se A è il doppio di B e B è un terzo di C,
quali sono i tre numeri?
9.
Sia a un numero naturale che diviso per 5 dà resto 3. Qual è il resto che si ottiene se si divide
per 5 il quadrato di a? e se si divide per 5 il triplo di a?