file - Istituto Italiano Edizioni Atlas

A
Problemi parametrici
La risoluzione di un problema può portare a scrivere un’equazione che contiene un parametro e in questo caso,
come abbiamo già visto nel capitolo sulle equazioni, non si vuole conoscere la soluzione, piuttosto quante soluzioni ammette il problema al variare del parametro. Vediamo un esempio.
Esempio
In una circonferenza di raggio r è inscritto un triangolo ABC nel quale la corda AB è lunga come il lato del
d ¼ x, determiniamo l’ampiezza degli angoli del triangolo in modo
triangolo equilatero inscritto. Posto CAB
pffiffiffi
che il suo perimetro sia uguale a kr 3, essendo k un numero reale positivo.
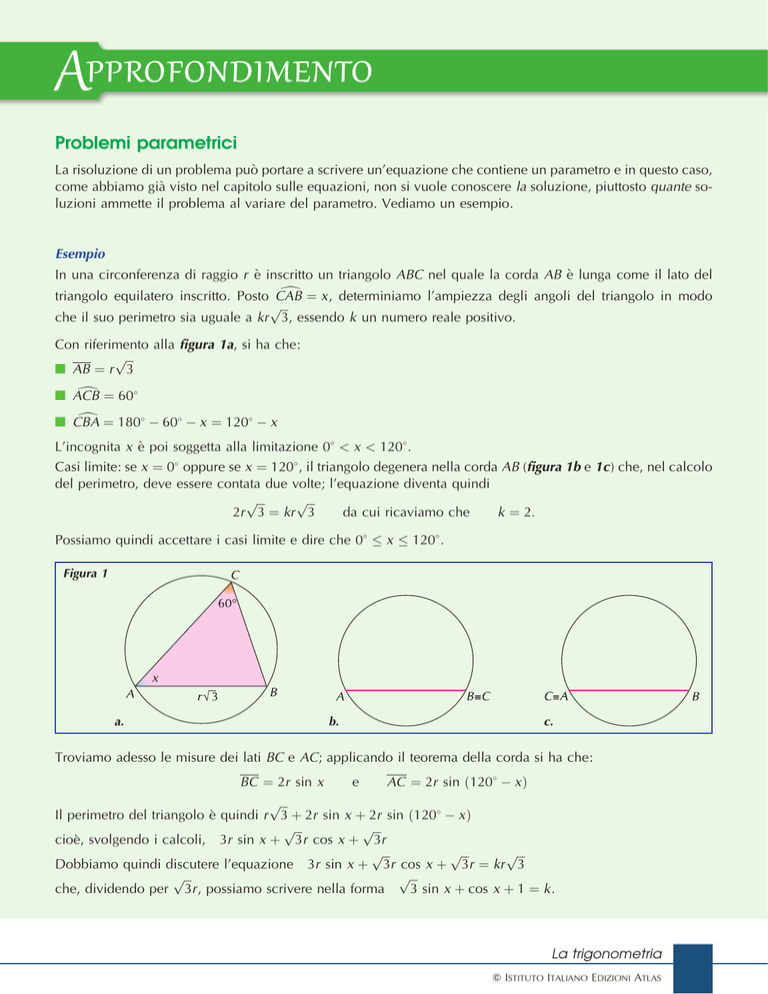
Con riferimento alla figura 1a, si ha che:
pffiffiffi
n AB ¼ r 3
d ¼ 60
n ACB
d ¼ 180 60 x ¼ 120 x
n CBA
L’incognita x è poi soggetta alla limitazione 0 < x < 120 .
Casi limite: se x ¼ 0 oppure se x ¼ 120 , il triangolo degenera nella corda AB (figura 1b e 1c) che, nel calcolo
del perimetro, deve essere contata due volte; l’equazione diventa quindi
pffiffiffi
pffiffiffi
2r 3 ¼ kr 3
da cui ricaviamo che
k ¼ 2:
Possiamo quindi accettare i casi limite e dire che 0 x 120 .
Figura 1
a.
b.
c.
Troviamo adesso le misure dei lati BC e AC; applicando il teorema della corda si ha che:
BC ¼ 2r sin x
e
AC ¼ 2r sin ð120 x Þ
pffiffiffi
Il perimetro del triangolo è quindi r 3 þ 2r sin x þ 2r sin ð120 x Þ
pffiffiffi
pffiffiffi
cioè, svolgendo i calcoli, 3r sin x þ 3r cos x þ 3r
pffiffiffi
pffiffiffi
pffiffiffi
Dobbiamo quindi discutere l’equazione 3r sin x þ 3r cos x þ 3r ¼ kr 3
pffiffiffi
pffiffiffi
che, dividendo per 3r, possiamo scrivere nella forma
3 sin x þ cos x þ 1 ¼ k.
La trigonometria
Q ISTITUTO ITALIANO EDIZIONI ATLAS
Si tratta di un’equazione lineare che, ponendo cos x ¼ X e sin x ¼ Y , e tenendo conto delle limitazioni per x,
dà luogo al seguente sistema
8 pffiffiffi
3Y þ X þ 1 ¼ k
>
>
< 2
X þ Y2 ¼ 1
>
>
: 1 X 1 ^ 0 Y 1
2
Dobbiamo quindi valutare le intersezioni della circonferenza con centro nelpffiffiffi
pffiffiffi
3
ðk 1Þ 3
l’origine e raggio 1 con il fascio di rette parallele Y ¼ Xþ
3
3
pffiffiffi
3
(angolo di inclinazione 30 ); riferendoci alla
di coefficiente angolare 3
figura 2, abbiamo che:
pffiffiffi 3
1
l la retta che passa per Að1, 0Þ passa anche per B
e si ottiene
,
2
2
per k ¼ 2 (abbiamo ritrovato il valore ottenuto nello studio dei casi limite)
l
Figura 2
la retta tangente si ottiene per k ¼ 3.
Abbiamo quindi sempre due soluzioni per 2 k 3.
ESERCIZI
1 Data la semicirconferenza di diametro AB ¼ 2r, siano AC e AD due corde tali che AD sia la bisettrice
d . Determina l’ampiezza dell’angolo CAB
d ¼ 2x in modo che il perimetro del quadrilatero
dell’angolo BAC
ACDB sia uguale a 4kr.
1k<
pffiffiffi
pffiffiffi
1þ 2
1þ 2
: una soluzione;
k 5 : due soluzioni
4
2
2
d ¼ 30 e la
2 Dal punto A di una semicirconferenza di diametro AB ¼ 2r conduci la corda AC tale che CAB
d ¼ x, con DAB
d > CAB;
d la perpendicolare DE condotta da D al diametro incontra
corda AD tale che DAB
AC in F. Discuti al variare di x la relazione DE þ FE ¼ kAF. Per quali valori di x il quadrilatero ABCD è
h
i
un trapezio isoscele?
k 1 : una soluzione; x ¼ 3
3 E’ data una semicirconferenza di centro O e diametro AB ¼ 2r; traccia la retta t tangente alla semicirconferenza in A, una corda AC e la bisettrice dell’angolo formato dalla tangente e da AC; siano poi
D il punto in cui la bisettrice incontra la semicirconferenza e P la proiezione di D su t.
a. Discuti, al variare del parametro k il numero di soluzioni dell’equazione CD þ DP ¼ kAB.
b. Tracciata da B la parallela al raggio OC che interseca in Q la retta AC, discuti la relazione
CB þ AQ ¼ kBQ.
(Suggerimento: b. osserva che i triangoli AOC e ABQ sono simili ed isosceli e che il rapporto di simi
pffiffiffi
pffiffiffi
1
2þ1
litudine è )
a. 0 k : una soluzione; b. 1 k < 2 : una soluzione; 2 k 5 : due soluzioni
2
2
4 Nel triangolo isoscele acutangolo ABC di base AC si ha che AB ¼ ‘; tracciate le tre altezze AD, BE, CF,
determina l’ampiezza 2x dell’angolo di vertice B in modo che sia BD þ BE þ BF ¼ kAB.
pffiffiffi
2
< k 3 : una soluzione
2
La trigonometria
Q ISTITUTO ITALIANO EDIZIONI ATLAS
5 Due circonferenze e 0 rispettivamente di centri O e O 0 e raggi r e r 0 sono tangenti esternamente in P e
4
si sa che OO 0 ¼ r; una retta s per P incontra la circonferenza in Q e la perpendicolare in O 0 alla retta
3
OO 0 in N. Determina l’ampiezza x dell’angolo formato dalla retta s e da OO 0 in modo che sia verificata
la relazione PQ þ 3PN ¼ kr.
Successivamente, detti H ed H 0 le proiezioni dei centri O e O 0 sulla retta s, indica in quale trasformazione si corrispondono i segmenti OH e O 0 H 0 .
pffiffiffi
2 2 k 3 : due soluzioni; k > 3 : una soluzione; omotetia di centro P e rapporto 1
3
pffiffiffi
6 Un triangolo ABC avente il lato AB che misura r 2 è inscritto in una circonferenza di raggio r. Determina l’ampiezza degli angoli del triangolo in modo che il suo perimetro sia uguale a
pffiffiffi
pffiffiffi 1 pffiffiffi
r 6 þ 3 2 þ 2 3 . Successivamente, determina un punto P sul minore dei due archi BC in modo
pffiffiffi
2
pffiffiffi
pffiffiffi
2
Ab ¼ 60 ; Bb ¼ 75 ; Cb ¼ 45 ; 3 3 k 3 : una soluzione
kPA.
che sia CP þ PB ¼
2
pffiffiffi
7 La corda AB di una circonferenza di raggio r misura 3r. Determina un punto C sul minore dei due archi
AB in modo che, condotta da A la corda AD perpendicolare ad AC, il perimetro del quadrilatero con
pffiffiffi pffiffiffi
vesso ACBD sia uguale a 3 þ 3 kr.
1 k 2 3 : due soluzioni
3
8 In una circonferenza di centro O e raggio r, la corda AB è il lato del triangolo equilatero inscritto. Traccia
d . Determina l’ampiezza
dal punto A le corde AC e AD in modo che AB sia bisettrice dell’angolo CAD
d in modo che l’area del quadrilatero ACBD sia uguale a 3 kr 2 .
dell’angolo CAB
2
0<k<
pffiffiffi
pffiffiffi
3
3
: una soluzione;
k 1 : due soluzioni
2
2
9 Siano P un punto di una semicirconferenza di centro O e diametro AB ¼ 2r, PH la perpendicolare condotta da P al diametro e OC il raggio perpendicolare ad AB; congiunto P con O, traccia da P la semiretta
d . Determina la posizione del
t che interseca OC in T in modo che PO sia la bisettrice dell’angolo HPT
punto P in modo che sia verificata la relazione PH ¼ 2kTO.
1 k 1 : due soluzioni simmetriche
4
10 Considerata la semicirconferenza di centro O e diametro AB ¼ 2r, sia P un punto posto sul prolungamento del diametro oltre B; tracciata da P la tangente alla semicirconferenza che la incontra in C, discuti,
2
al variare del parametro k, la relazione
4
CP
k
ð
Þ
2 þ 1 ¼ 2 Area AOC .
r
OP
½k > 4 : una soluzione
11 Nella semicirconferenza di centro O e diametro AB ¼ 2r, sia P il punto medio del raggio AO; traccia da
P una semiretta che forma con AB un angolo x e che incontra la semicirconferenza in C. Dall’estremo A
traccia poi la corda AD parallela a PC e sia E la proiezione ortogonale di D su PC.
2
2
a. Discuti, al variare del parametro k, il numero di soluzioni dell’equazione AD þ DE ¼ krPE.
7 2
r .
b. Determina poi per quale valore di x l’area del trapezio APDE vale
32
"
k > 8 : una soluzione;
3
#
rffiffiffiffi
5 k 8 : due soluzioni; x ¼ 15
3
3
12 Del triangolo ABC isoscele di vertice C si sa che AC ¼ a; traccia l’altezza CH relativa alla base AB, e da
H le parallele ai lati obliqui che incontrano AC in N e CB in M. Dopo aver stabilito la natura del quad ¼ 2x :
drilatero HMCN e aver posto ACB
La trigonometria
Q ISTITUTO ITALIANO EDIZIONI ATLAS
a. determina il valore di x per il quale AreaðHMCN Þ ¼ k CB
b. trova per quale valore di x l’area suddetta è massima.
2
1
0 < k < : due soluzioni; x ¼ 45
4
13 È dato un triangolo equilatero ABC di lato 2‘; sul lato AC ed esternamente al triangolo, costruisci la semicirconferenza di diametro AC. Da un punto P dell’altezza AH traccia la perpendicolare ad AC che
d ¼ x, discuti, al variare di P su AH, la relazione
incontra AC in Q e la semicirconferenza in R. Posto CAR
pffiffiffi
3þ2 3
0<k
: una soluzione
4
AP
.
AR þ AQ ¼ k‘
PQ
14 In una semicirconferenza di centro O e diametro AB ¼ 2r, una semiretta s uscente da A incontra in C la
semicirconferenza e in D la tangente alla semicirconferenza nel punto B; sia E il punto d’incontro di DB
d ¼ x in modo
con la tangente alla semicirconferenza nel punto C. Determina l’ampiezza dell’angolo CAB
che sia verificata la relazione CE þ CD ¼
1
kCB.
2
½una soluzione limite x ¼ 0 per ogni k; k > 1 : una soluzione
15 Assegnato il settore circolare AOB di raggio r e ampiezza 3 , sia Q un punto dell’arco AB e H e K le
4
proiezioni ortogonali di Q rispettivamente su AO e OB in modo che K e H appartengano ai segmenti AO
e OB. Discuti, al variare del parametro k, il numero di soluzioni dell’equazione QK QH ¼ kOK OH.
pffiffiffi
k 3 þ 2 2 : due soluzioni
pffiffiffi
16 In una circonferenza di raggio r, traccia la corda AB lunga r 3 e la retta t tangente alla circonferenza in
B. Preso un punto P nel minore dei due archi AB, indica con H e K le proiezioni di P rispettivamente
sulla corda AB e sulla retta t. Discuti al variare del parametro reale k la relazione PH PK ¼ 2kr. Per
quale posizione di P i due segmenti PH e PK risultano uguali?
pffiffiffi
2 33
3
k < 0 : una soluzione; 0 k due soluzioni; PH ¼ PK con P B e con P punto medio dell’arco AB
4
4
17 Due circonferenze di centri O e O 0 sono tangenti internamente in S (O è il centro della circonferenza
maggiore). Una semiretta t uscente da S incontra la circonferenza più interna in M 0 e quella più esterna
in M; la perpendicolare a t uscente da S incontra la circonferenza più interna in N 0 e quella più esterna in
d in modo che
N. Sapendo che SM þ SN 0 ¼ 8SO e posto OS ¼ r, determina l’ampiezza dell’angolo MSO
sia verificata la relazione SO 0 ¼ kSO.
pffiffiffiffiffiffi
15 k 4 : due soluzioni; k > 4 : una soluzione
18 Data una retta r, prendi su di essa un punto A e da A traccia due semirette s e t fra loro perpendicolari e
giacenti nello stesso semipiano rispetto a r. Prendi poi un punto B su s e un punto C su t in modo che sia
d in
AB ¼ 2AC. Indicate con M e N le proiezioni di B e C su r, determina l’ampiezza dell’angolo BAM
2
modo che sia verificata la relazione: area ðBCNMÞ ¼ kAC . Stabilisci poi quale deve essere l’ampiezza
di tale angolo affinchè l’area richiesta sia massima.
9
1k
4
: due soluzioni; x ¼
4
19 In una circonferenza di diametro AB ¼ 2r, considera la corda CD, lato dell’esagono regolare inscritto, e
d ¼ x, dicongiungi C con A e D con B in modo da ottenere il quadrilatero convesso ABDC. Posto BAC
scuti, al variare del parametro k, il numero di soluzioni dell’equazione 2pðABDCÞ ¼ kr.
pffiffiffi
3 þ 3 k 5 : una soluzione
20 Sul lato AB di un quadrato ABCD di lato ‘ ed esternamente ad esso costruisci la semicirconferenza di dia 2
2
2
2
metro AB. Determina un punto P sulla semicirconferenza in modo che sia PD þ PC ¼ k PA þ PB .
½3 k 5 : due soluzioni
La trigonometria
Q ISTITUTO ITALIANO EDIZIONI ATLAS
21 Data una circonferenza di centro O e raggio r, sia t la semiretta ad essa tangente in un suo punto A; considera poi la corda AB tale che l’angolo da essa formato con la semiretta t sia di 30 . Preso un punto C su
d in modo che sia verificata la relazione AC 2 þ BC 2 ¼ kAB 2 .
t, determina l’ampiezza dell’angolo COA
5 k 1 : due soluzioni; k > 1 : una soluzione
8
22 Siano AB, BC e CD tre corde consecutive di una circonferenza di centro O raggio r, rispettivamente lato
del quadrato inscritto, lato dell’esagono inscritto e lato del triangolo equilatero inscritto. Preso sull’arco
pffiffiffi
d ¼ x, studia il numero di soluzioni dell’equazione PD þ 2 AP ¼ kAD al
AD un punto P e posto PBA
variare del parametro k.
1k
pffiffiffi
2 : una soluzione
23 In una circonferenza di centro O e diametro AB ¼ 2r considera la corda CD perpendicolare ad AB ed
uguale al lato del triangolo equilatero inscritto e indica con H la sua intersezione con AB (con
d ¼ x, discuti, al vaAH < HBÞ. Preso un punto P sul prolungamento di AB, dalla parte di B e posto CPA
riare del parametro k la numerosità delle soluzioni dell’equazione CP þ HP ¼ kCD.
pffiffiffi
2þ 3
: una soluzione
k
2
La trigonometria
Q ISTITUTO ITALIANO EDIZIONI ATLAS