Limiti da problemi sul triangolo isoscele

Verso l’Esame di Stato nel Liceo Scientifico
Limiti da problemi sul triangolo isoscele
(triangolo isoscele con angolo di 135°)
Problema
Sia ABC un triangolo isoscele con l’angolo nel vertice C di ampiezza 135° e i cui lati congruenti misurano a.
Si consideri sul lato BC un punto P e indicata con x la misura del segmento CP si studi il seguente limite
lim
P C
AP  AC
CP
Risposta:
2
2
Elaborazioni
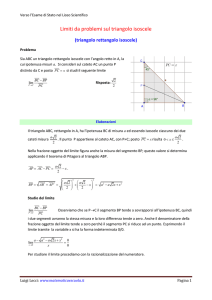
Facciamo riferimento alla figura riportata a lato.
Determiniamo la misura del segmento AP.
1) Il triangolo isoscele ha l’angolo nel vertice C comune
ai lati congruenti di ampiezza 135°, quindi ciascuno
degli angoli alla base AB ha ampiezza (180°135°)/2=22°30’;
2) M è il punto medio della base AB e dal triangolo
rettangolo AMC ricaviamo

 45 
AM  AC  cos  2230'  a  cos   .
 2 
Utilizzando la formula di bisezione per l’angolo acuto =22,5° ricaviamo
cos   
1  cos  2 
2

1  cos  45 
2

1
2
2
2 
2 2
2 2
, quindi risulta AM  a 
2
2
3) Considerando il triangolo rettangolo PHB, essendo PB  CB  CP  a  x ricaviamo
HP  PB  sen  2230'
sen    
1  cos  2  
2
e tenendo conto della formula di bisezione per l’angolo acuto =22,5°

1  cos  45 
2

2 2
2 2
si ricava HP  PB  sen  2230'   a  x  
.
2
2
Ricaviamo ora la misura del cateto HB. Risulta HB  PB  cos  2230'   a  x  
2 2
.
2
4) Determiniamo ora la misura del segmento AH:
AH  AB  HB  2 AM  HB  a  2  2   a  x  
Luigi Lecci: www.matematicaescuola.it
2 2

2
2 2 
ax
2
Pagina 1
Verso l’Esame di Stato nel Liceo Scientifico
5) Applicando ora il teorema di Pitagora al triangolo rettangolo APH troviamo la misura del
segmento AP (ipotenusa) .
2
2
ax 
2 2 


 

a

x

AP  AH  HP   2  2 




2  
2



1
1
2  2  a 2  2ax  x 2   2  2  a 2  2ax  x 2   ... 
4 x 2  4a 2 x  4a 2 
2
2
2

2



x2  a 2x  a2
Studio del limite richiesto
lim
P C
AP  AC
, che assume la forma
CP
lim
x 0
x2  a 2 x  a2  a
,
x
perché quando PC la misura del segmento CP tende a zero.
Osservazione geometrica.
Notiamo che quando PC il segmento AP si sovrappone al lato AC del triangolo, quindi la misura
del segmento AP tende alla misura del lato AC, dunque la differenza AP  AC tende a zero.
Il limite in esame si presenta nella forma indeterminata 0/0.
Per studiare la forma indeterminata procediamo con la razionalizzazione del numeratore
moltiplicando numeratore e denominatore per il fattore razionalizzante
Seguono le elaborazioni.


x2  a 2x  a2  a .
2
x2  a 2x  a2  a2
x2  a 2x  a2  a x2  a 2x  a2  a
lim

 lim

x 0
x 0
x
x2  a 2x  a2  a
x x2  a 2x  a2  a
lim
x 0
x


x xa 2

x  a 2x  a  a
2
2




a 2
2

2a
2
Luigi Lecci: www.matematicaescuola.it
Pagina 2